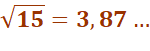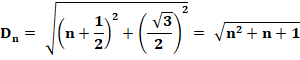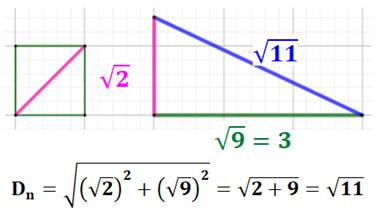|
Édition du: 18/01/2024 |
Faites un double-clic pour un retour en haut de page
![]()
|
Constructions de la racine des nombres Méthodes
générales et méthodes plus spécifiques pour construire la racine
carrée des nombres. Exemples
|
||||
|
|
Sommaire de cette page Méthodes générales (pour tout nombre) >>> Méthode générale pour racine de n >>> Méthode générale en spirale >>> Méthode avec somme de quatre carrés Méthodes particulières >>> Méthode des arcs de cercles >>> Méthode des carrés >>> Méthode des carrés en diagonale >>> Méthode des losanges à 60° >>> Bilan |
Débutants Glossaire |
||
Voir Brève
53-1059 / Brève 57-1125
Méthodes générales
|
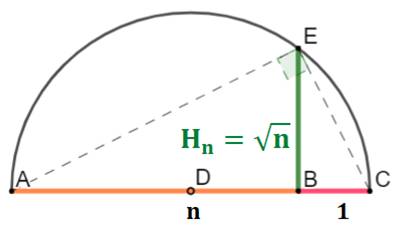
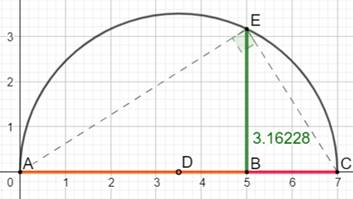
La méthode la plus simple pour construire la
racine carrée d'un nombre n quelconque consiste à construire cette figure en
demi-cercle:
Note: n n'est pas nécessairement un nombre entier. |
EB² = AB × BC |
||
|
Nombres composés Dans ce cas, il est plus pratique de matérialiser
le produit en AB et BC: Avec cet exemple: AB= 5 et BC = 2; |
|
||
|
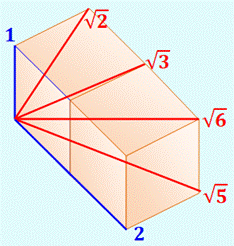
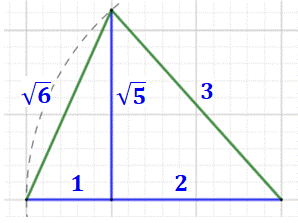
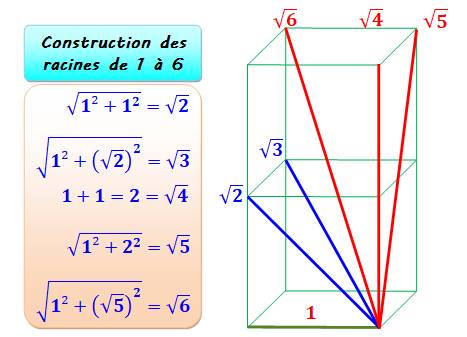
Figure particulière en racine de 5
et racine de 6 Construction:
|
|
||
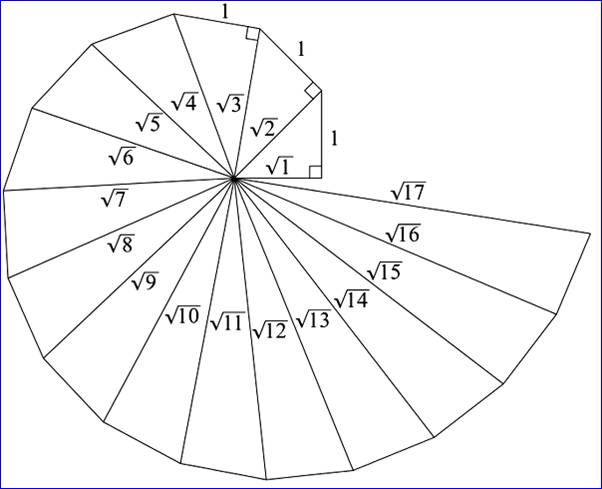
Voir Escargot
de Pythagore pour explications
|
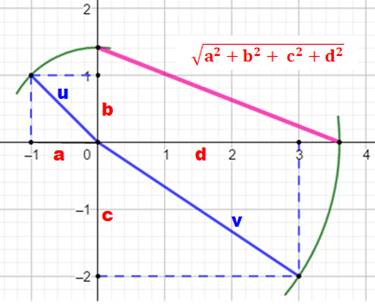
Tout nombre est somme
de quatre carrés. Prenons le nombre 15: Construction Placez un couple de valeur en abscisse de part et
d'autre de l'origine (a et d, par exemple) L'autre couple sur l'axe des ordonnées. Les diagonales sont nommées u et v et leurs
longueurs sont reportés sur les axes (arcs verts). Le segment (rose) qui joint les intersections
avec les axes est notre racine (ici racine de 15) Justification
|
|
|
Voir Explications
complémentaires et autres exemples
![]()
Méthodes particulières
|
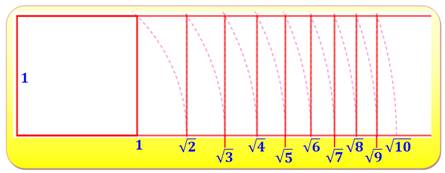
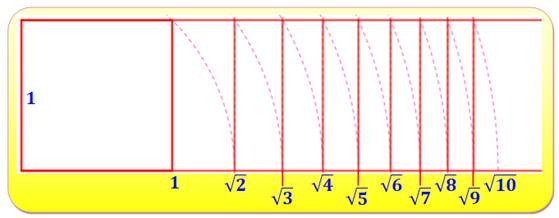
Construction Carré unité. Arc de cercle avec la diagonale pour rayon. L'intersection en bas
produit la racine de 2 (longueur de la diagonale du carré unité). Etc. |
|
|
Voir Brève
53-1059
|
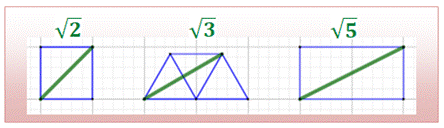
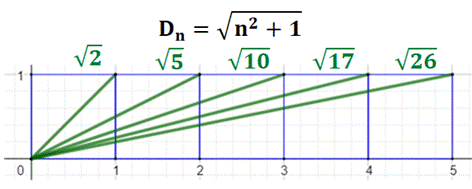
Avec des carrés unités mis côte à côtes, il est
possible de construire les racines de n² + 1. Soit la suite des nombres: 2, 5, 10, 17, 26, 37, 50, 65, 82, 101, 122, 145,
170, 197, 226, 257, 290, 325, 362, 401 |
|
|
|
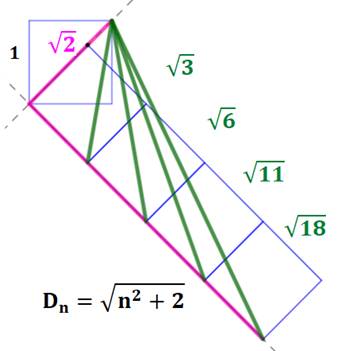
On construit un premier carré pour disposer de sa
diagonale qui mesure racine de 2. Sur cette diagonale, on construit des carrés
accolés. Les segments verts mesurent racine de n² + 2 avec n la quantité de carrés utilisés. La suite des nombres sous radical est : |
|
|
|
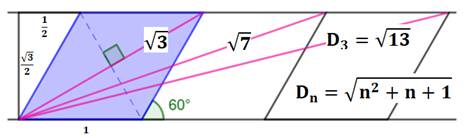
On construit une suite de triangles
équilatéraux accolés et de côté unité (angles 60°). Ils forment d'abord un losange,
puis des parallélogrammes
(losanges accolés). Les diagonales roses pour n losanges accolés
mesurent successivement: 3, 7, 13, 21, 31, 43, 57, 73, 91, 111, 133, 157,
183, 211, 241, 273, 307, 343, 381, 421, … |
|
|
|
Plusieurs méthodes On sait construire la racine de n'importe quel
nombre avec le demi-cercle. On sait construire différents nombres avec les
carrés et les losanges.
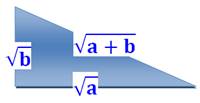
Sachant construire la racine de a et la racine de
b, on sait construire la racine de (a + b) en construisant le triangle
rectangle ayant (racine de a) et (racine de b) pour longueurs des côtés. Exemple avec racine de 11 Construction avec report de la
diagonale avec un compas
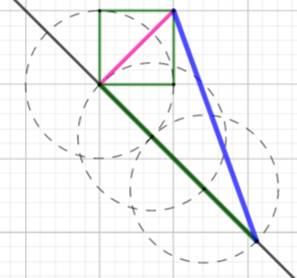
Construction avec copie de cercles
unitaires
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |