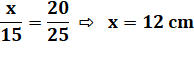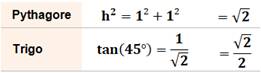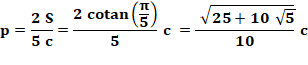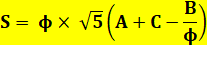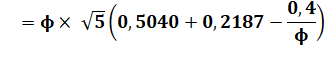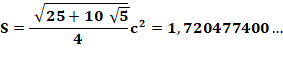|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
BRÈVES de MATHS – Page 46 Un millier de faits et chiffres sur les nombres et les
mathématiques
En principe ces pages sont très abordables sans
connaissances particulières de maths. Elles sont proposées dans un ordre
quelconque favorisant la découverte de sujets multiples. |
Anglais: Facts and figures about numbers and mathematics
900. Cordes égales |
|
|||
|
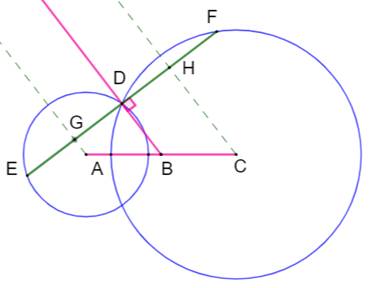
Problème Deux cercles sécants en D. Construire une sécante en D découpant deux cordes
de même longueur. Construction Milieu B de AC, segment joignant les deux
centres. Demi-droite BD. Perpendiculaire en D à BD. Intersections E et F. ED = DF. Explications Les trois parallèles AG, BD et CH découpent sur
GH la même proportion 1/2 que sur AC. GD = DH Toutes les parallèles sont perpendiculaires à EF. Les cordes ED et DF sont coupées en leur milieu. GD = DH =
> ED = DF. |
|
|||
|
Brèves associées |
>>>
Centre du cercle |
>>>
Brèves Constructions – Index |
||
|
Pour en savoir plus |
>>>
Cercles et sécantes |
>>>
Cercle – Index |
||
901. Aire inter-segments |
|
|||
|
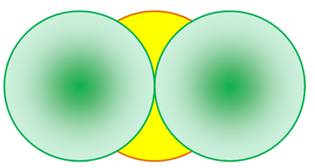
Question Quelle
est l'aire de la zone jaune appartenant au cercle central occulté par ces
deux cercles verts, tangents et de même rayon unité ? |
|
|||
|
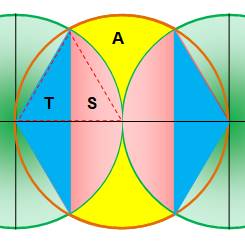
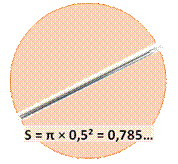
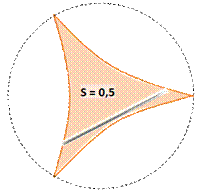
Solution, la piste L'aire cherchée correspond à celle du cercle
rouge dont on retire quatre fois l'aire des segments S (rose).
Or le secteur S + T, avec un angle de 120°,
représente un tiers de l'aire du disque. En retirant l'aire de T, deux fois le triangle rectangle, on
calcule l'aire de S. Tous calculs faits:
|
|
|||
|
Brèves associées |
>>>
Sangaku à deux cercles inscrits |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Aire inter-segment – Calcul détaillé |
>>>
Aire du secteur |
||
902. Carrés avec allumettes |
|
||
|
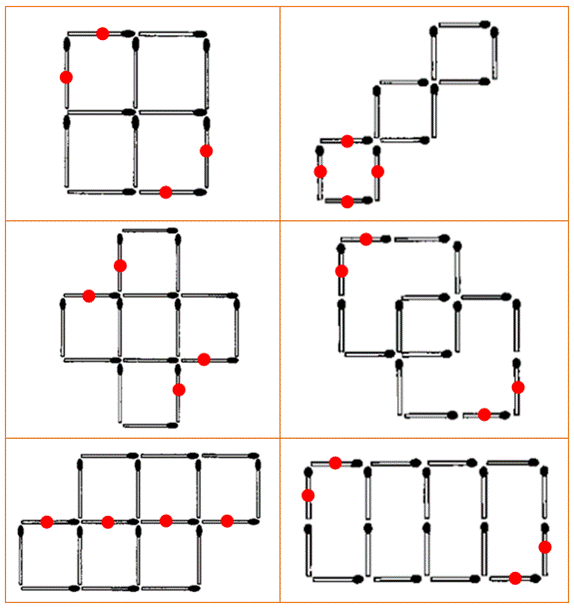
Défis Déplacer quatre allumettes à gauche pour former
trois carrés. Solution à droite avec points rouges pour les
allumettes déplacées.
|
|||
|
Brèves associées |
>>> Ampoules et trois interrupteurs |
>>>
Brèves Énigmes – Index |
|
|
Pour en savoir plus |
>>>
Allumettes en carrés |
>>>
Jeux avec allumettes |
|
903. Dissection du pentagone |
|
|||
|
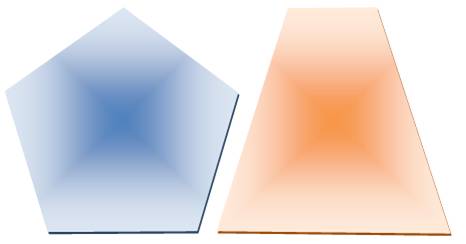
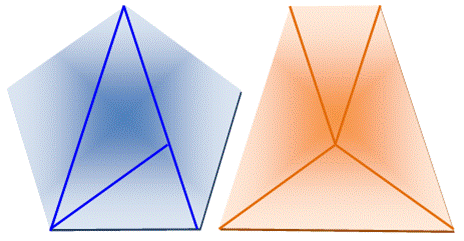
Énigme Découpez le pentagone régulier en quatre
triangles isocèles, et Formez un trapèze isocèle. |
|
|||
|
Solution Les triangles isocèles ne sont pas tous les
quatre de la même taille. |
|
|||
|
Brèves associées |
>>>
Pentagone – Énigme avec les angles |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Pentagone et trapèze isocèle |
>>>
Trapèze |
||
904. Carré magique avec dominos |
|
|||
|
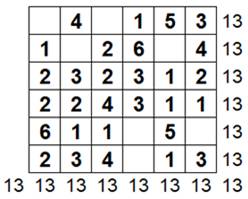
Carré magique avec 18 dominos.
|
|
|||
|
Brèves associées |
>>> Carré
magique à la demande |
>>>
Brèves Carrés Magiques – Index |
||
|
Pour en savoir plus |
>>>
Carrés magiques et dominos |
>>>
Carrés magiques – Index |
||
905. Araignée sur une boite |
|
|||
|
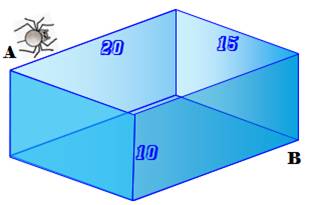
Énigme Une boite fermée est posée sur le sol. Une araignée en A détecte un bon repas en B. Comment y aller par le plus court chemin ? Solution Le chemin le plus court consiste à parcourir deux
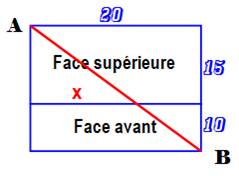
des faces en oblique (illustration en bas): L² = 20² + (15 + 10)² = 400 + 625 = 1025 L = 32,015… cm Point de bifurcation
Attention: ce n'est pas
10/15 de 20 ! Pour information Le trajet le long des arêtes aurait donné: 45 cm Celui en pure diagonale: D² = 20² + 15² + 10² = 400 + 225 + 100 = 725 D = 26,92… cm |
Araignée voulant aller de A à B
Trajet le plus court pour
l'araignée
|
|||
|
Brèves associées |
>>> Aire des parallélogrammes |
>>>
Brèves Énigmes – Index |
||
|
Pour en savoir plus |
>>>
Trajet le plus court pour la fourmi >>>
Fourmi sur le cylindre |
>>>
Théorème de Thalès |
||
906. Cinq carrés pour un carré |
|
|||
|
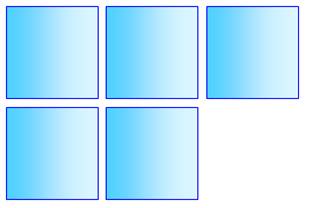
Énigme On dispose de cinq carrés. Comment les assembler
pour former un seul grand carré ? Vous n'avez droit qu'à un seul coup de cutter en
ligne droite. Solution Empiler quatre carrés et les couper selon le
trait rouge qui rejoint un sommet au milieu du côté opposé.
Assembler le carré restant et les huit morceaux
découpés selon la figure du bas. |
Cinq carrés
Le grand carré à partir des cinq
petits
|
|||
|
Brèves associées |
>>> Carré divisé – Aire manquante |
>>>
Brèves Énigmes – Index |
||
|
Pour en savoir plus |
>>>
Carré divisé en cinq |
>>>
Dissections |
||
907. Chiffre deviné |
|
|||
|
Tour de magie Pense à un nombre de quatre chiffres. Soustrait chacun des chiffres. Barre un chiffre de ce résultat et donne-moi les
trois autres. Je peux te dire quel est le chiffre que tu as
barré. Explications Un nombre auquel on a retiré ses chiffres est
divisible par 9 et, dans un nombre divisible par 9, la somme des chiffres est
un multiple e 9. Il suffit de trouver le chiffre à ajouter pour restituer
un multiple de 9. |
Exemple Un nombre: 1289 Sans ses chiffres: 1289 – (1+2+8+9) = 1269 On barre le 6 et on annonce: 1, 2, 9 Le nombre manquant est 6, car 1 + 2 + 9 = 12 et 1
+ 2 = 3; le complément à 9 est 6. Exemple si le 9 avait été barré On donne alors: 1, 2, 6 = > somme 9 Complément à 9: c'est le 0 ou le 9 qui a été
barré. Il y a ambiguïté. Exemple délicat Un nombre: 4567 => 4545 On barre 4 et on donne: 4, 5, 5 => 15 => 4 Complément à 9: c'est un 4 qui a été barré. |
|||
|
Brèves associées |
>>>
Deviner deux nombres |
>>>
Brèves Magie – Index |
||
|
Pour en savoir plus |
>>>
Preuve par 9 |
>>>
Divisibilité par 9 |
||
908. Céviennes et binôme |
|
|||
|
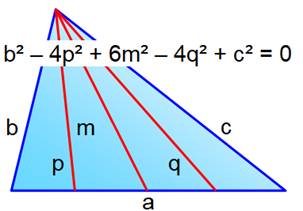
Céviennes régulières Les céviennes régulières sont issues du même
sommet et découpent des segments égaux sur le côté opposé au sommet. Binôme de Newton La figure donne un exemple avec k = cinq segments issus du sommet
supérieur. La relation indiquée, du type de celle des
identités de Newton, donne un résultat nul. Cela est vrai pour n'importe quelle valeur de k
supérieure à 2. |
Cas de trois céviennes régulières
Les coefficients sont ceux
du binôme de Newton. |
|||
|
Brèves associées |
>>>
Droites dans le triangle |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Céviennes régulières >>>
Binôme de Newton |
>>>
Médianes |
||
909. Parallélogramme et cousin |
|
|||
|
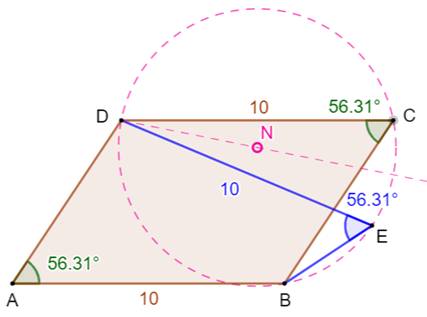
Cousin du parallélogramme Cette idée provient de la question: Si un
quadrilatère à deux de ses angles opposés égaux et deux de ses côtés de même
longueur, est-il forcément un parallélogramme ? La réponse est non: il y a deux quadrilatères qui
répondent à cette spécification. Construction Un parallélogramme ABCD. Cercle passant par les points B, C et D. Angle NDC reporté pour former NDE. Interceptant le même arc BD, l'angle en E est
égal à celui en C. Le segment DE est de même longueur que le segment
DC, du fait que DN est la bissectrice et qu'elle offre une symétrie. Le quadrilatère ABED répond aussi aux
spécifications. Il est le cousin du parallélogramme. |
Deux quadrilatères cousins
Quadrilatères ABCD et ABED:
mêmes angles opposés et même longueur des côtés opposés |
|||
|
Brèves associées |
>>>
Parallélogramme (Règle du -) |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Parallélogramme >>>
Formules du parallélogramme |
>>>
Angles dans le cercle >>> Divers défis de
géométrie |
||
910. Rectangle trigonométrique |
|
|||
|
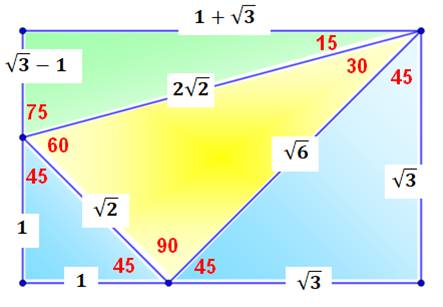
Quatre triangles en un rectangle Un rectangle qui encapsule quelques propriétés
fondamentales de la trigonométrie à partir de calculs avec le simple théorème
de Pythagore. Exemple Avec le triangle rectangle isocèle (45°) de côté
unité, on a:
|
|
|||
|
Brèves associées |
>>>
Valeurs trigo. principales |
>>>
Brèves Trigonométrie – Index |
||
|
Pour en savoir plus |
>>>
Angles et trigonométrie >>>
Trigonométrie – Bases |
>>>
Théorème de Pythagore >>>
Trigonométrie
en première |
||
911. Quatrième parcelle |
|
|||
|
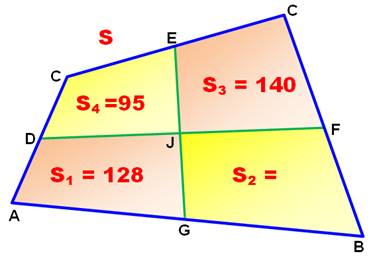
Énigme On donne un quadrilatère dont trois surfaces sont
connues (en cm²) comme indiqué. Les points E, F, G et H sont les milieux des
côtés (EG et DF sont les médianes). Trouvez la valeur de l'aire du quatrième
quadrilatère (S2). Solution S1 +
S3 = S2 + S4 128 + 140 = x + 95 x = 268 – 95 = 173 cm² et S = 268 x 2 = 536 cm² |
|
|||
|
Brèves associées |
>>> Rectangle en neuf – Périmètre |
>>>
Brèves Énigmes – Index |
||
|
Pour en savoir plus |
>>>
Quatrième parcelle – Explications |
>>>
Sixième segment |
||
912. Apothème du pentagone |
|
|||
|
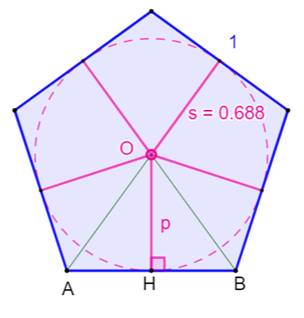
L'apothème
p est le rayon du cercle inscrit au
pentagone de côté c. Si S est l'aire
du pentagone, c'est aussi l'aire des cinq triangles du type OAB dont l'aire
vaut: ½ p·c On en déduit la longueur de l'apothème:
|
|
|||
|
Brèves associées |
>>>
Pentagone – Énigme avec les angles |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Pentagone et ses mensurations |
>>>
Apothème du décagone |
||
913. Pentagone et trois triangles |
|
|||
|
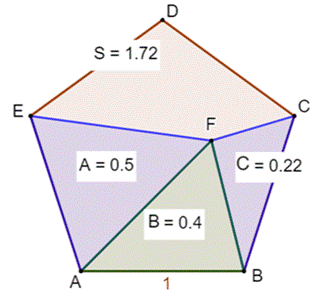
Problème On connait l'aire des trois triangles A, B et C. Donner l'aire S du pentagone régulier. Solution La solution passe par la connaissance et la
démonstration de cette formule impliquant le nombre d'or (phi):
Vérification avec la formule de
l'aire du pentagone
|
Exemple de situation numérique A, B et C sont connus; il faut trouver S.
Il est possible de calculer l'aire du pentagone
régulier par la seule connaissance des aires des triangles A, B et C. |
|||
|
Brèves associées |
>>> Aire mystère du triangle |
>>>
Brèves Énigmes – Index |
||
|
Pour en savoir plus |
>>>
Démonstration de la formule >>>
Pentagone régulier |
>>>
Nombre d'or |
||
914. Carré et deux cercles |
|
|||
|
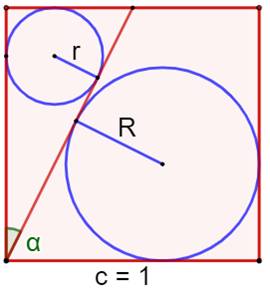
Problème Un carré unité (c = 1) et une
"semi-diagonale" joignant un sommet au milieu du côté opposé. Les cercles inscrits dans les deux régions du
carré. Quel est le rapport entre les rayons r et R de
ces cercles? Solution – Indices Le principe consiste à montrer que les rayons R
et r tels que sur la figure font partie de triangles rectangles semblables au
grand triangle rectangle de la figure. Puis, à considérer le rectangle ayant les deux
centres comme sommets opposés. |
|
|||
|
Brèves associées |
>>> Cercles – Tangence au diamètre |
>>>
Brèves Énigmes – Index |
||
|
Pour en savoir plus |
>>>
Solution |
>>>
Autres défis |
||
915. Roméo et Juliette |
|
|||
|
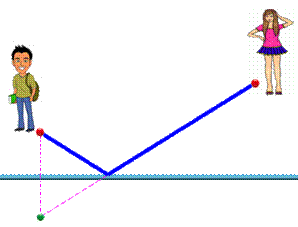
Problème Roméo doit apporter une cruche d'eau fraiche à
Juliette. Quel est le plus court chemin ? Solution Si Roméo était de l'autre côté de la rivière, en
position symétrique, le plus court chemin serait la ligne droite. Avec Roméo du même côté que Juliette, le trajet
le plus court est le même, sauf que la partie de l'autre côté de la rivière
doit être pris dans sa position miroir (symétrique). |
|
|||
|
Brèves associées |
>>>
Périmètre inconnu (Paris-Marseille…) |
>>>
Brèves Énigmes – Index |
||
|
Pour en savoir plus |
>>>
Trajet le plus court |
>>>
Symétries |
||
916. Les trois chiens |
|
|||
|
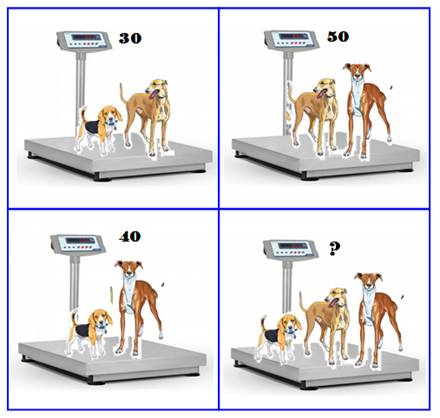
Problème Les chiens font l'objet des pesées indiquées. Quel est le poids des trois chiens objet de la
quatrième pesée ? Solution Une solution avec des équations est possible. Mais,
il existe une solution beaucoup plus simple. En effet, si l'on ajoute les résultats des trois
pesées, on obtient: 30 + 40 + 50 = 120 kg. Or, cela correspond à deux fois les trois chiens. Le poids des trois chiens est donc: On en déduit facilement le poids de chacun en
calculant le poids du manquant à chaque pesée: 10, 20 et 30kg. |
|
|||
|
Brèves associées |
>>> La vente des œufs |
>>>
Brèves Énigmes – Index |
||
|
Pour en savoir plus |
>>>
Équations pour débutants |
>>> Exercices au collège |
||
917. Aiguille de Kakeya |
|
||
|
Disque Une aiguille de longueur unité. Elle doit faire un tour complet dans le plan. Si on fait pivoter l'aiguille autour de son
centre, la surface balayée est un disque. Est-ce que l'aire balayée est la plus petite ?
NON ! Deltoïde La deltoïde est la trajectoire d'un point d'un
cercle lorsque celui-ci roule sans glisser à l'intérieur d'un cercle trois
fois plus grand. L'aiguille tourne avec ses deux extrémités
parcourant deux arcs tandis qu'elle reste tangente au troisième arc. La réduction de la surface balayée est
importante, mais il existe mieux … L'aire balayée peut être rendue aussi
petite que l'on veut. |
|
||
|
Brèves associées |
>>>
Cercle de Conway |
>>>
Brèves Géométrie – Index |
|
|
Pour en savoir plus |
>>>
Aiguille de Kakeya – Explications |
>>>
Disque >>> Deltoïde |
|
918. Puissance des nombres successifs |
|
||||
|
Triangulaires Un nombre triangulaire d'ordre n est la somme de
tous les nombres jusqu'à n. Un hypertriangulaire est calculé de la même
manière mais en élevant chaque nombre à sa puissance. Factorielles Un nombre factoriel d'ordre n est le produit de
tous les nombres jusqu'à n. Un hyperfactoriel est calculé de la même manière
mais en élevant chaque nombre à sa puissance. |
Quatre types de nombres Somme ou
produit des nombres successifs avec ou
non leur puissance
Curiosité L'hyperfactorielle 5 est le nombre de
millisecondes en un jour. H5! = 11 × 22 × 33 × 44 ×
55 |
||||
|
Brèves associées |
>>>
Nombres friables |
>>>
Brèves Types de Nombres – Index |
|||
|
Pour en savoir plus |
>>>
Hypertriangulaires et hyperfactorielles |
>>>
Factorielles – Index |
|||
919. Spirales du pentagone |
|
|||
|
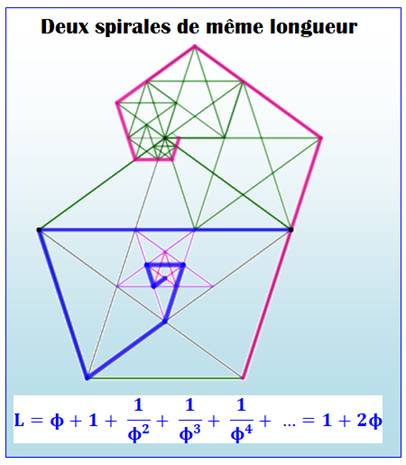
Pentagones gigognes Une suite de pentagones de plus en plus petits,
chacun formé sur le précédent. Spirales On forme une spirale interne (bleue) et une
spirale externe (rose). La première commence par une diagonale et la
seconde par un côté prolongé. Leur longueur commune est égale au nombre d'or. Longueur La longueur de chaque branche est égale aux
puissances successives de l'inverse du nombre d'or. La longueur
de ces deux spirales tend vers
deux fois le nombre d'or augmenté de l'unité. |
|
|||
|
Brèves associées |
>>>
Spirale de Théodore de Cyrène |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Calcul de la longueur limite |
>>>
Pentagone >>>
Nombre d'or dans le pentagone |
||
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()