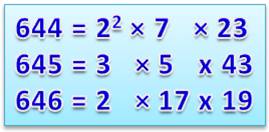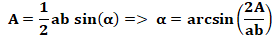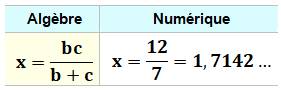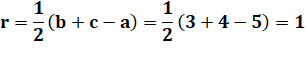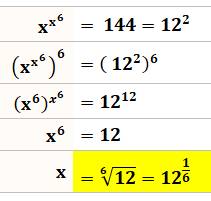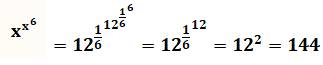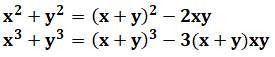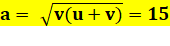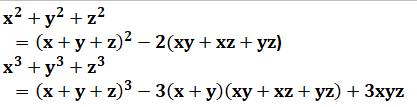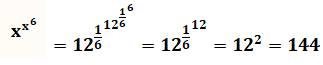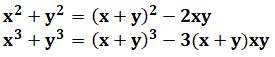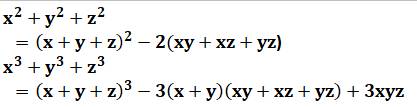|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
BRÈVES de MATHS – Page 52 Un millier de faits et chiffres sur les nombres et les
mathématiques
En principe ces pages sont très abordables sans
connaissances particulières de maths. Elles sont proposées dans un ordre
quelconque favorisant la découverte de sujets multiples. |
Anglais: Facts and figures about numbers and mathematics
1020. Facteurs distincts |
|
|||
|
Facteurs distincts Tout nombre se décompose en un produit unique de
nombres appelés facteurs: 10 = 2 × 5; 20 =
2² × 5. Les deux nombres 10 et 20 ont deux facteurs
différents, distincts 2 et 5. Quantité de facteurs distincts Le nombre 644 est le plus petit nombre ayant la
propriété suivante: chacun des trois nombres successifs ont trois facteurs
distincts. |
Trois facteurs distincts
Cinq facteurs distincts Plus petite
suite de cinq nombres: |
|||
|
Brèves associées |
>>> Diviseurs
d'un nombre |
>>>
Brèves Opérations – Index |
||
|
Pour en savoir plus |
>>>
Quantité de facteurs distincts |
>>>
Nombre 644 |
||
1021. Énigme 84:81 |
|
||
|
Résoudre cette énigme parue dans la presse en
mi-2023
Source Carnet
Psy – Nathalie Martinez – 09 07 2023 |
|||
|
Brèves associées |
>>>
Énigmes virales en brèves |
>>>
Brèves Énigmes – Index |
|
|
Pour en savoir plus |
>>>
Énigmes virales sur Internet |
>>>
Défis mathématiques – Index |
|
1022. Rectangle en trois triangles |
|
|||
|
Trois triangles de même aire Cette dissection est impossible: pas trois
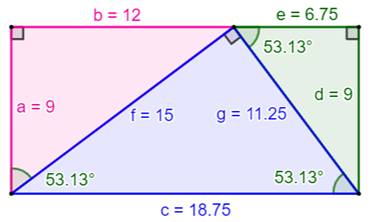
triangles de même aire dans le rectangle. Trois triangles semblables Cette dissection est impossible pour le carré et elle
l'est pour un rectangle dont la longueur est au moins deux fois sa largeur. Il s'agit alors de trois triangles rectangles
tels que disposés sur la figure. Si a et b sont les longueurs des côtés d'un de
ces triangles, alors les dimensions du rectangle sont:
|
Exemple de partage en trois
triangles semblables
|
|||
|
Brèves associées |
>>> Rectangle dans le triangle rectangle |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Rectangle en triangles – Explications |
>>>
Triangles dans rectangle |
||
1023. Carré magique multiplicatif |
|
|||
|
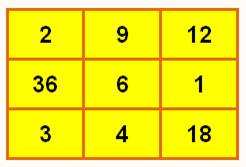
Carré magique multiplicatif d'ordre
3 Ce carré a sans doute été trouvé en 1893 par G.
Pfeffermann. Il est cité par Harry A. Sayles en 1913. Sa constante magique est 216, nombre qui est le plus
petit possible, démontré en 1983. Propriétés Comme tout carré magique multiplicatif, celui-ci
reste magique lorsque chacun des nombres est élevé à la puissance k. Il est impossible de construire un carré magique
multiplicatif avec des nombres entiers consécutifs. Le plus petit inclut les
nombres: 1, 2, 3 et 4. |
Le plus petit carré magique
multiplicatif
Les
produits des lignes, colonnes et diagonales sont égaux à 216 = (2 × 3)3. |
|||
|
Brèves associées |
>>> Carré
magique additif 3x3 |
>>>
Brèves Jeux de grilles – Index |
||
|
Pour en savoir plus |
>>>
Carrés magiques multiplicatifs |
>>>
Carrés magiques – Index |
||
1024. Partage du carré en triangles |
|
|||
|
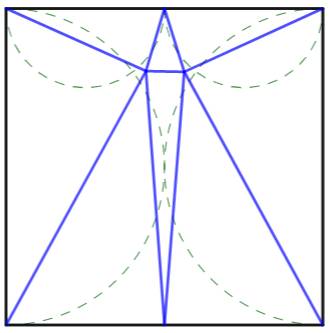
Problème ancien Comment partager le carré en triangles acutangles
(tous ses angles sont aigus) ? Solution La figure montre une solution possible. Les traits en pointillés verts montrent les zones
d'exclusion du sommet interne des triangles. Par exemple, si le sommet est situé à l'intérieur
du demi-cercle, l'angle est obtus; il est droit s'il est situé sur le
demi-cercle; il est aigu au-delà. Lindgren, Cassidy et Lord ont montré que la
meilleure solution exige huit triangles. La partition est toujours possible pour tout
nombre pair supérieur ou égal à 8. |
Partage du carré en triagles
acutangles
Un minimum de huit triangles
est nécessaire. |
|||
|
Brèves associées |
>>> Carré
– Partage en sept |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Partage du carré |
>>>
Types de triangles |
||
1025. Fraction avec exposants |
|
||
|
Comment simplifier ces fractions avec exposants ? Règles et exemples
Applications
|
|||
|
Brèves associées |
>>> Factorisation (a – c)(b – a)(c – b) |
>>>
Brèves Algèbre – Index |
|
|
Pour en savoir plus |
>>>
Règles de calcul avec les exposants |
>>> Bases de
l'algèbre |
|
1026. Division de fractions |
|
||
|
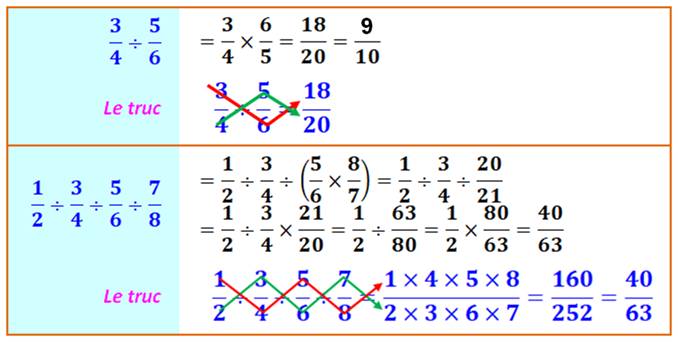
Comment calculer la division de fraction en
cascade.
|
|||
|
Brèves associées |
>>> Fraction – Construction géométrique |
>>>
Brèves Opérations – Index |
|
|
Pour en savoir plus |
>>>
Division des fractions |
>>>
Fractions – Index |
|
1027. Triangles et ses trois côtés |
|
||||
|
Bonne nouvelle …
|
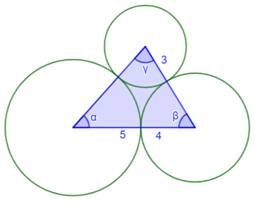
Défi des trois cercles tangents
Calculer la valeur des trois angles. |
||||
|
Brèves associées |
>>>
Triangle de Conway – Calculs |
>>> Brèves
Géométrie – Index >>>
Défis de géométrie – Index |
|||
|
Pour en savoir plus |
>>>
Défi des trois cercles tangents – Solution >>>
Résolution LLL des triangles |
>>>
Formule de Héron >>>
Formule de l'aire en sinus |
|||
1028. Volume du cube évidé |
|
|||
|
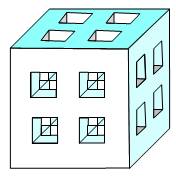
Cube à 3 perforations (n = 1 trou
par côté)
Dénombrement On compte simplement les cubes présents:
Total: 20 Si le côté des petits cubes vaut 1 cm, le volume
du cube évidé est égal à 20cm3. |
Cube à 12 perforations (n = 2 trous
par côté)
Le volume du cube évidé, ici pour n = 2, est égal
à 81. Volume en fonction de n trous par
côté Vn = { 20, 81, 208, 425, 756,
1225, 1856, …} Diviseurs de 240k Cette suite de nombre est aussi la quantité de
diviseurs de 240 à la puissance k:
|
|||
|
Brèves associées |
>>>
Carrés dans une grille – Quantité |
>>>
Brèves Dénombrement – Index |
||
|
Pour en savoir plus |
>>>
Volume du cube évidé – Explications |
>>>
Cube |
||
1029. Carrés en 5 |
|
|||
|
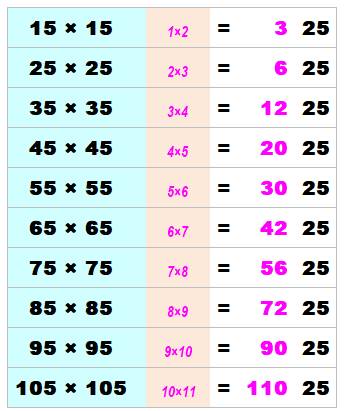
Truc de calcul mental Le carré d'un nombre terminé par 5 est facile à
calculer:
Explications Un nombre terminé par 5 peut s'écrire: Son carré: On a bien les centaines isolées du nombre 25. On note que le principe de calcul s'étend à tous
les nombres terminés par 25. |
|
|||
|
Brèves associées |
>>> Carrés des nombres en 5 |
>>>
Brèves Calcul mental – Index |
||
|
Pour en savoir plus |
>>>
Calcul mental des carrés en 5 |
>>> Calcul
mental – Index |
||
1030. Carrés des nombres en 100+n |
|
|||
|
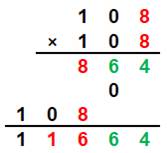
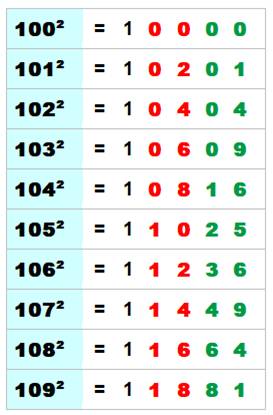
Truc de calcul mental Le carré d'un nombre en 100 + n est facile à
calculer:
Explications La disposition des chiffres se dévoilent
immédiatement en posant la multiplication:
Avec l'algèbre, on remarque
que: |
Carré avec double
et carré de l'unité dans se ses chiffres
|
|||
|
Brèves associées |
>>> Multiplication de nombres proches de 100 |
>>>
Brèves Calcul mental – Index |
||
|
Pour en savoir plus |
>>>
Calcul mental des carrés |
>>>
Multiplications mentales >>>
Multiplications posées |
||
1031. Produit de puissances: 8^6×5^5=? |
|
|||
|
Défi Calculer ce produit sans calculette. Commentaires On utilise les propriétés du calcul avec des
exposants. La première ligne fait la somme 6 = 5 + 1. La suivante regroupe les puissances de 5. Ces deux
mêmes puissances peuvent être associées: ak ٠bk = (a ٠
b)k. L'opération inverse est opérées sur 405
= (4 × 10)5. Le nombre 4 est égal 2 au carré et 45 = (2²)5
= 210. Même chose avec 8 qui vaut 23. Les puissances de 2 sont associées: 210
× 23 = 210+3 = 213. On sait que 210
= 1024. Alors, 211 = 2048; 212
= 4 096 et 213 = 8 192. |
Calculs
|
|||
|
Brèves associées |
>>> Calcul avec des puissances |
>>>
Brèves Calcul – Index |
||
|
Pour en savoir plus |
>>>
Calculs (pratiques) avec des exposants |
>>>
Puissances des nombres |
||
1032. Quatre cubes |
|
|||
|
Propriété de base On connait la somme des cubes de 3, 4, 5 qui donne le cube de 6.
Quatre nombres qui se suivent. Généralisation Cette propriété est reconduite en ajoutant le même chiffre à chacun
des termes. |
Identités
|
|||
|
Brèves associées |
>>> Repdigits en 3 au cube |
>>>
Brèves Motifs – Index |
||
|
Pour en savoir plus |
>>>
Nombre 6 en puissances |
>>>
Somme de cubes >>> Pépites numériques |
||
1033. Résoudre ce triangle rectangle |
|
|||
|
Question On connait u = 16 et v = 9. Calculer a et b. Piste Calculer la longueur de CH en remarquant que les triangles AHC et CHB
sont semblables. Solution
Explications: suivre le lien
ci-dessous |
|
|||
|
Brèves associées |
>>>
Triangle rectangle – Carrés inscrits |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Résolution de ce triangle rectangle |
>>>
Résolution des triangles |
||
1034. Cercle inscrit dans le triangle rectangle |
|
|||
|
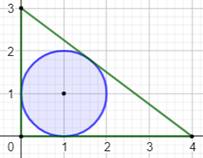
Construction Un triangle rectangle et son cercle inscrit. Valeur du rayon en fonction de a, b et c ? Piste Les segments reliant un point aux points de
tangence à un cercle sont égaux. Appliquer ce théorème aux trois sommets du
triangle. Exprimer l'hypoténuse a en fonction des longueurs
des deux segments de tangence. |
|
|||
|
Calculs
|
Exemple avec le triangle rectangle
(3, 4, 5)
|
|||
|
Brèves associées |
>>>
Carrés et quatre cercles |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Cercles et triangle rectangle |
>>>
Théorème des tangentes |
||
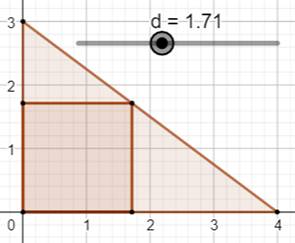
1035. Carré dans le triangle rectangle |
|
|||
|
Question Quelle est la taille maximale du carré construit
de cette manière dans un triangle rectangle? Piste On note que les triangles rectangles de cette
figure sont semblables. On utilisera le théorème de Thalès qui précise
des proportions. Solution
|
|
|||
|
Brèves associées |
>>> Carré divisé – Aire manquante |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Carré dans le triangle rectangle |
>>> Triangle
et cercle |
||
1036. Sommes en repdigits |
|
|||
|
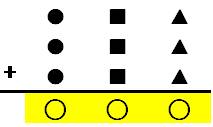
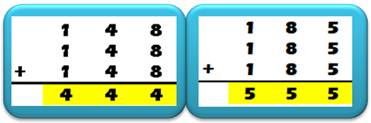
Question Quelles sont les solutions de cette opération ? Il existe deux solutions (148 et 185) pour
lesquelles le chiffre ◯ est égal à l'un
des chiffres du nombre. Généralisation Il existe dix solutions avec ◯ égal un chiffre quelconque et avec deux, trois, … opérandes dans la
somme. Certaines sont triviales comme 2 × 222 = 444. |
Deux solutions originales
Dix solutions
|
|||
|
Brèves associées |
>>> Repdigits en 2 au cube |
>>>
Brèves Motifs – Index |
||
|
Pour en savoir plus |
>>>
Repdigits – Additions |
>>>
Repunits |
||
1037. Deux cercles dans un carré |
|
|||
|
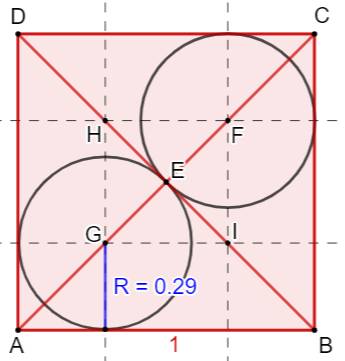
Construction Un carré de côté unité et ses diagonales. Deux cercles inscrits dans les triangles formés
avec l'une des diagonales. Quel est le rayon des cercles Calculs
|
|
|||
|
Brèves associées |
>>>
Carrés et quatre cercles |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Deux cercles et carré |
>>>
Deux cercles et triangle |
||
1038. Inconnu en puissance |
|
|||
|
Question Résoudre: x^x^6 = 144 Pistes Utiliser les règles de calcul des expressions avec exposants. Intuition de départ : 144 est le carré de 12. Essayons de former des puissances "équivalentes" de chaque
côté de l'égalité. Pour y arriver, élevons les deux membres de l'égalité à la puissance
6. |
Calcul
Vérification
|
|||
|
Brèves associées |
>>> Calcul avec racines carrées |
>>>
Brèves Algèbre– Index |
||
|
Pour en savoir plus |
>>>
Calcul avec des exposants |
>>>
Puissances et exposants |
||
1039. Polynômes symétriques |
|
|||
|
Polynôme symétrique Un polynôme symétrique reste invariant en
inversant ses variables. Les polynômes symétriques sont ceux du premier degré.
Ils sont trois, par exemple, pour trois variables: X + Y + Z XY + YZ + ZX XYZ Racines des équations Il existe une relation entre les racines d'un
polynôme et ces polynômes élémentaires. Exemple avec aX3 +
bX2 + cX + d = 0 X1 + X2 + X2 =
-b/a X1 X2 + X1 X3
+ X2 X3 = c/a X1 X2 X3 = -d/a |
Théorème fondamental des fonctions
symétriques Soit un polynôme symétrique à n variables, alors
il existe une unique fonction polynomiale
combinant ses n fonctions symétriques élémentaires. Exemples
|
|||
|
Brèves associées |
>>> Factorisation de a^n + b^n |
>>>
Brèves Algèbre– Index |
||
|
Pour en savoir plus |
>>>
Polynômes symétriques |
>>> Polynômes |
||
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()