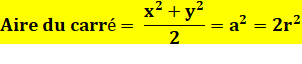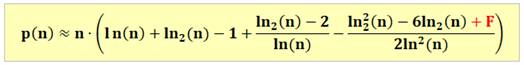NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 03/10/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 10		Page 20		Page 30		Page 40			Page 50
	Page 40 (780-799)		Page 41 (800-819)		Page 42 (820-839)		Page 43 (840-859)		Page 44 (860-879)
	Page 45 (880-899)		Page 46 (900-919)		Page 47 (920-939)		Page 48 (940-959)		Page 49 (960-979)

BRÈVES de MATHS – Page 47

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

920. Cercle et cercle tangent au diamètre
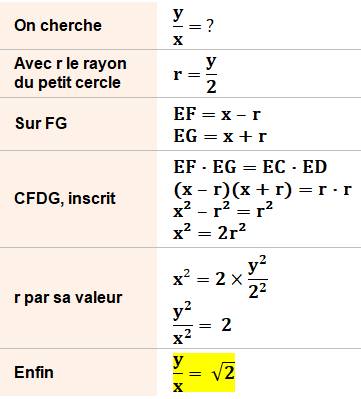
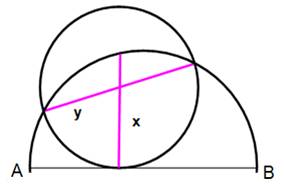
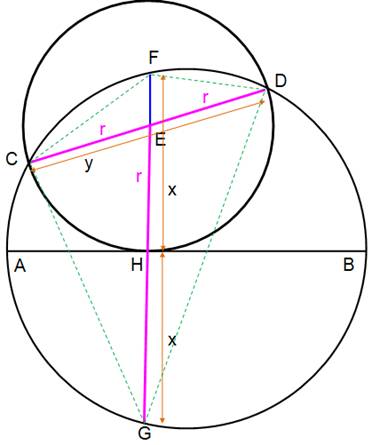
Énigme Un cercle et un de ses diamètres AB. Un cercle tangent à ce diamètre AB en un point quelconque du diamètre. Quel est le rapport entre les longueurs des segments en rose ? Solution (Voir notations) Rayon du petit cercle: r Corde CD: y = 2r Demi-corde: FH = x On mise sur la propriété des segments de diagonales d'un quadrilatère inscriptible. Calcul		Le défi: y / x = ? Notations
Brèves associées	>>> Cercle interne au carré – Rayon ?		>>> Brèves – Énigmes – Index
Pour en savoir plus	>>> Quadrilatère inscriptible >>> Défis en géométrie		>>> Cercles – Index >>> Défis divers

921. Faire 10 avec k fois le 9
Défis avec chiffres imposés Il existe de nombreux jeux qui consistent à atteindre un nombre comme le résultat d'opérations impliquant des chiffres contraints. Le plus célèbre est le jeu du quatre fois 4. Faire tous les nombres de 1 à une valeur maximale en utilisant quatre chiffres 4. 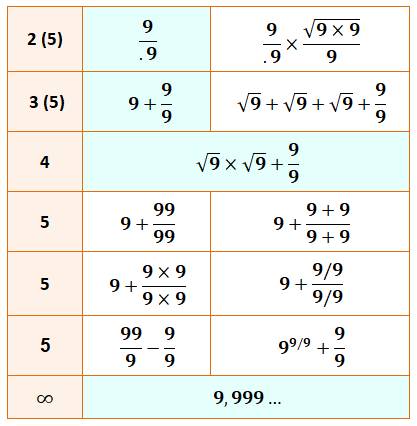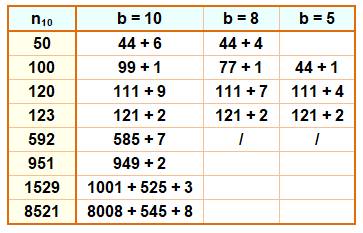Ex: 10 = (44 – 4) / 4 Celui du 100 avec tous les chiffres est aussi très célèbre: Ex: 10 = 1 + 2 + 3 – 4 + 5 + 6 + 78 + 9 Défi du 10 en cinq 9 Celui-ci (tableau) fait partie de toute une panoplie d'autres défis, en l'occurrence faire 10 avec cinq fois le chiffre 9. Le tableau indique aussi les possibilités pour deux, trois ou une infinité de 9.		En colonne rose, la quantité de chiffres utilisée.
Brèves associées	>>> Opérations avec les chiffres		>>> Brèves – Motifs – Index
Pour en savoir plus	>>> Jeu du quatre 4 >>> Jeu du 100 en chiffres		>>> Jeux et défis avec les chiffres – Index >>> Nombe 10 >>> Pourquoi 0,999… = 1

922. Cercle, carré et cordes
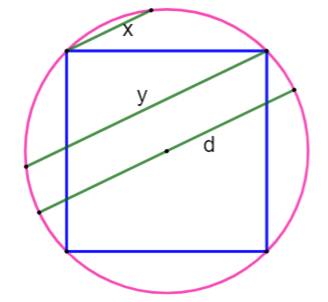
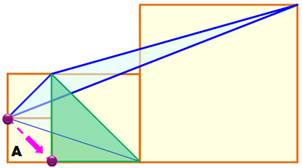
Construction Un carré inscrit dans le cercle. Un diamètre quelconque. Deux cordes parallèles à ce diamètre, et issues des sommets du carré. Propriété Avec a le côté du carré et r le rayon du cercle. L'aire du carré inscrit (bleu) est égale à la demi-somme des aires des carrés construits sur les cordes.
Brèves associées	>>> Rayon et cordes sécantes		>>> Brèves – Géométrie – Index
Pour en savoir plus	>>> Cercle, carré et cordes		>>> Arcs, cordes et sagittas

923. Triangle en carrés
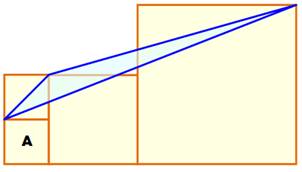
Énigme Quatre carrés disposés comme indiqué. Les deux plus petits ont une aire égale à A. Le grand carré est de taille quelconque. Quelle est l'aire du triangle bleu ? Indice Deux triangles de même base et dont le troisième sommet se trouve sur une parallèle à la base ont des aires égales. Trouvons donc des triangles d'aires équivalentes. Figure du centre La diagonale du grand carré est parallèle à celle du petit carré qui se trouve être un côté du triangle. 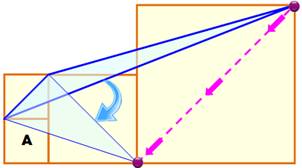Le sommet éloigné de ce côté est translaté le long de la diagonale jusqu'en bas, tout en conservant, donc, l'aire du triangle. Les deux triangles bleus ont même aire. Figure du bas Renouvelons l'opération avec la diagonale du petit carré inférieur. Le sommet gauche est translaté sur la diagonale jusqu'en bas; le triangle conserve son aire, car la diagonale du petit carré est parallèle à la diagonale du carré central. Le triangle vert a même aire que le triangle de départ. Solution L'aire du carré central est égale à 4A. L'aire du triangle est égale à 2A.
Brèves associées	>>> Trois cercles dans un rectangle		>>> Brèves – Énigmes – Index
Pour en savoir plus	>>> Triangle en carrés		>>> Carré et deux triangles

924. Un carré penché sur trois carrés
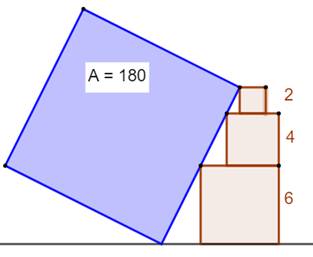
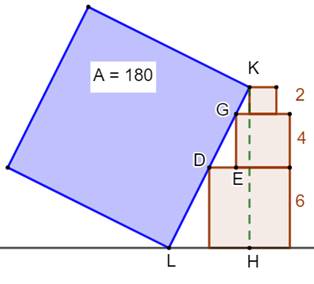
Problème Un carré oblique reposant sur une tour de trois carrés. Aire du carré bleu (Confirmez le 180) ? Solution (Voir illustration du bas)
Brèves associées	>>> Carré et deux cercles		>>> Brèves – Géométrie – Index
Pour en savoir plus	>>> Énigmes avec des carrés		>>> Carrés

925. Monde du nano
Brèves associées	>>> Quantité de sable dans l'Univers	>>> Brèves – Sciences – Index
Pour en savoir plus	>>> Nanotechnologies	>>> Gravure des circuits intégrés

926. Factorisation de Fermat
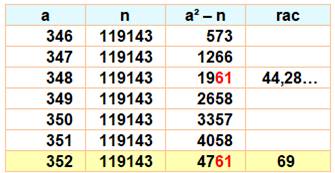
Reconnaitre le carré d'un nombre L'unité d'un carré n'est jamais 2, 3, 7 ou 8. Les carrés ne se terminent que par les deux derniers chiffres du tableau ci-contre. Factoriser (exemple) On demande de factoriser le nombre 119 143 dont on indique que les facteurs premiers sont proches. Alors ces facteurs sont autour de la racine: 346. Quelques essais avec des nombres proches de 346 permettent de trouver la solution (tableau du bas). D'abord, calculer B = a² – n jusqu'à trouver un carré b². On arrive sur 1961 dont les deux derniers chiffres sont compatibles avec un carré. Calcul de la racine. Non, ce n'est pas un carré. On continue et on trouve 4761 = 69² et b = 69. La factorisation est immédiate: a² – b² = (a – b)(a + b) = (352 – 69)(352 + 69) = 283 x 421 = 119 143		Deux derniers chiffres des carrés Exemple de factorisation
Brèves associées	>>> Produit de deux nombres proches		>>> Brèves – Opérations – Index
Pour en savoir plus	>>> Factorisation de Fermat		>>> Carrés – Index >>> Unités des puissances

927. Impair = différence de carrés
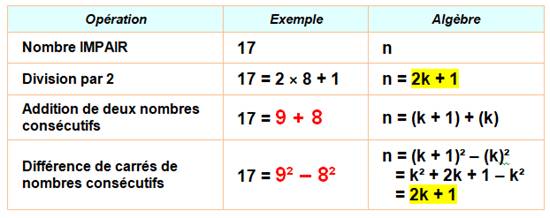
Tout nombre impair est somme de deux nombres consécutifs. Il est aussi égal à la différence des carrés de ces deux nombres consécutifs.
Brèves associées	>>> Carré = Somme de cubes		>>> Brèves – Puissance – Index
Pour en savoir plus	>>> Nombres et différences de carrés		>>> Différence de carrés

928. Table du 7 et clavier numérique
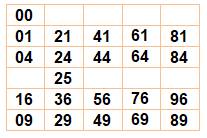
La table du 7 peut offrir une certaine résistance à la mémorisation. Un truc peut vous aider: l'utilisation du clavier numérique. On y trouve les unités des multiplications dans l'ordre. Voyez l'illustration. Lire la dizaine avec l'unité sur le clavier.
Brèves associées	>>> Multiplication par 7		>>> Brèves – Opérations – Index
Pour en savoir plus	>>> Multiplication par 7 >>> Divisibilité par 7		>>> Tables de multiplications

929. Énième premier en formule ?
Question Peut-on trouver le nombre premier de rang n en calculant une formule ? Non, mais on peut s'en rapprocher.		Formule du théorème des nombres premiers Le nombre premier p de rang n est approximativement égal au rang multiplié par son logarithme naturel. Cette évaluation produit une approximation très grossière. Ex: p(1000) = 7 919 alors que la formule donne 7 797. Formule améliorée Cette formule donne un nombre premier proche toujours inférieur. Ex: 7 840 pour p(1000) = 7 919.
Meilleure réponse En 2017, Christina Adler démontre que deux formules encadrent parfaitement le énième nombre premier à partir d'un certain rang.		En réalisant ces trois calcul successivement, on trouve: Avec F = 11, la valeur est proche de p(n); mieux que 10^-5. Avec F = 10,667, elle donne une borne inférieure. Avec F = 11,508, elle donne une borne supérieure.
Brèves associées	>>> Quantité de premier – Fonction Pi(n)		>>> Brèves – Premiers – Index
Pour en savoir plus	>>> Encadrement des nombres premiers >>> Théorème des nombres premiers		>>> Logarithmes

930. Nombres: Somme & Produit
Deux nombres Quels sont les deux nombres tels que leur somme S = 16 et leur produit P = 55 ? La solution passe par la résolution d'une équation du second degré ou plus simplement par application de cette formule: (x – y)² = (x + y)² – 4 xy Exemple: S = 16, P = 55 (x –y)² = 16² – 4 × 55 = 256 – 220 = 36 = 6² Avec x + y = 16 et x – y = 6 => x = 11 et y = 5		Plusieurs nombres Quels sont les nombres distincts tels que S = 20 et P = 300 ? Les mêmes nombres forment l'addition et la multiplication. Ce sont des diviseurs de P. Diviseurs de 300: 2, 3, 4, 5, 6, 10, 12, 15, 20, 25, 30, 50, 60, 75, 100, 150. Une combinaison de ces nombres doit produire une somme égale à 20. Seule possibilité: S = 2 + 3 + 5 + 10 dont le produit est bien 300. En admettant des "1", on trouverait aussi: 6 + 5 + 5 + 2 + 1 + 1 et d'autres.
Brèves associées	>>> Somme de consécutifs (4+5+6 = 7+8)		>>> Brèves – Motifs – Index
Pour en savoir plus	>>> Somme-produit avec deux nombres >>> Somme-produit avec k nombres		>>> Diviseurs >>> Jeux avec les nombres – Index

931. N = pal + pal + pal
Théorème des nombres polygonaux On sait que (Fermat 1636): Tout nombre entier est la somme de, au plus, k nombres k-gonal. de trois nombres triangulaires, de quatre nombres carrés, de cinq nombres pentagonaux, etc. Théorèmes des nombres palindromes On a prouvé en 2016 et 2017 que: Tout nombre est la somme de trois palindromes en base b (b > 4) et de quatre pour b à partir de 2.		Exemples Nombres sommes de trois palindromes au plus selon la base.
Brèves associées	>>> Théorème des nombres polygonaux		>>> Brèves – Th. des Nbs – Index
Pour en savoir plus	>>> Palindrome		>>> Bases de numération

932. Divisibilité par 5
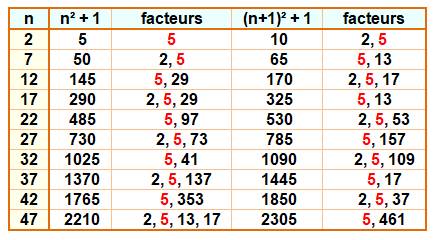
Propriété de divisibilité Si un nombre divise à la fois n² + 1 & (n + 1)² + 1 alors ce nombre est 5. Commentaires Le tableau montre le facteur commun pour les cas de n qui satisfont une divisibilité. Il s'agit toujours du nombre 5. NB. on donne les facteurs, sans leur puissance éventuelle.		Exemples pour n de 1 à 50
Brèves associées	>>> Divisibilité des carrés et cubes		>>> Brèves – Th. des Nbs – Index
Pour en savoir plus	>>> Divisibilité et nombre 5		>>> Divisibilité par 5

933. Bicarrés
Propriété Tout bicarré (puissance quatrième d'un nombre) est la somme de groupes d'entiers successifs selon une disposition incrémentale régulière. Construction Sélectionner k nombres successifs une fois sur deux, avec k + 1 à chaque itération. Avec n paquets retenus, la somme de ces n paquets vaut n^4.		Exemple pour 2^4 k = 1 => 1 ce nombre est conservé; k = 2 => 2 et 3 sont éliminés; k = 3 => 4, 5, 6 sont conservés Soit deux groupes retenus La somme de ces nombres vaut: 1 + 4 + 5 + 6 = 16 = 2^4 Avec trois groupes, on aurait la puissance 3; avec k groupes la puissance k.
Table montrant la construction des quatre premiers bicarrés
Brèves associées	>>> Carrés et le nombre 5		>>> Brèves – Opérations – Index
Pour en savoir plus	>>> Bicarrés et sommes		>>> Cubes

934. Racines à étages
Énigme – Résoudre cette équation avec des racines emboitées Astuce ! Voyez comme la partie rouge "infinie" est équivalente à la racine "infinie" de l'équation d'origine. On peut donc remplacer l'une par l'autre et même par sa valeur 2.
Brèves associées	>>> Racine cubique – Calcul mental	>>> Brèves – Opérations – Index
Pour en savoir plus	>>> Bases de l'algèbre	>>> Racines continues

935. Premiers records
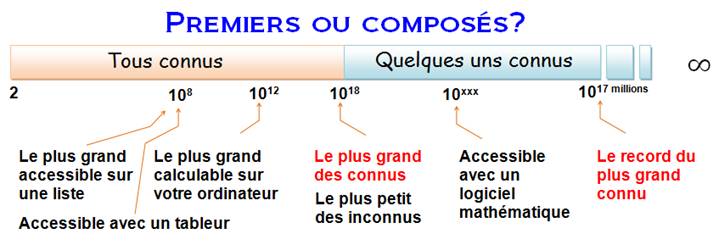
La barre "tous connus" (10^18) veut dire que tous ces nombres inférieurs sont connus en tant que composés ou premiers. Il s'agit d'une limite inférieure car il suffit que quelqu'un s'y attelle et le plafond peut vite s'élever. Intérêt minime, car il est assez rapide de pratiquer un test par calcul sans avoir à recourir à de longues tables encombrantes.
Brèves associées	>>> Quantité de premier – Fonction Pi(n)	>>> Brèves – Premiers – Index
Pour en savoir plus	>>> Grands nombres premiers	>>> Nombres premiers – Index

936. Chemins de la TOUR (échecs)
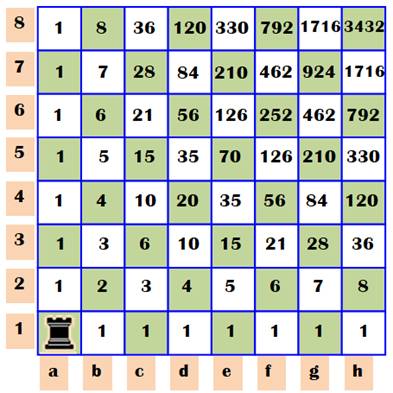
La tour doit atteindre la case h8 Elle peut prendre différents chemins. Combien ? Pour aller en b2, elle peut passer par a2 ou par b1, soit deux chemins. On écrit 2 dans la case b2. Pour aller en c2, elle peut aller directement en c1 (1 chemin) ou alors aller en b2 (2 chemins), soit 1 + 2 = 3 chemins. Etc. Chaque valeur est égale à la somme des valeurs des cases à gauche et en bas. Pour arriver en h8, il y a 3 432 chemins. Le tableau, avec ses diagonales, est un sous-ensemble du triangle de Pascal.
Brèves associées	>>> Échiquier tronqué		>>> Brèves – Jeux – Index
Pour en savoir plus	>>> La tour aux échecs		>>> Jeux et énigmes – Index

937. Conjecture des premiers jumeaux
En 2013, Yitang Zhang démontre qu'il existe une infinité de nombres premiers avec un intervalle de 70 millions. En 2015, James Maynard améliore le résultat de Yitang Zhang en prouvant que la conjecture est vraie pour tout intervalle supérieur à 600, puis à 243. Pour prouver la conjecture, il faudrait descendre à 2. En 2022, Yitang Zhang affirme avoir résolu une version faible de la conjecture de Landau-Siegel, équivalente à la célèbre conjecture de Riemann qui prouverait que l'intervalle est 2. Publication non encore approuvée.		Une façon de compter les nombres premiers est de les répartir en un nombre fini de groupes selon leurs congruences mod p, p étant un nombre premier. Par exemple, lorsque p = 5, les nombres premiers se répartissent en quatre groupes selon que le reste de leur division par p vaut 1, 2, 3 ou 4. Cela est possible avec un échantillon de nombres premiers suffisamment grand; mais quelle est la taille de l'échantillon? Sans doute très grand, et augmentant exponentiellement avec p. En 1936, Carl Ludwig Siegel, mathématicien allemand, a trouvé une formule relativement simple liée à ce problème de distribution des nombres premiers, qui rend les échantillons nécessaires potentiellement beaucoup plus petits. Il a montré que si, dans certaines circonstances, sa formule ne donnait pas 0, cela revenait à prouver la conjecture. Edmund Landau ayant obtenu le même résultat, ce problème est devenu la conjecture des zéros de Landau-Siegel. Ce que Yitang Zhang prétend avoir prouvé est une version plus faible, mais qui aurait des conséquences similaires concernant la distribution des nombres premiers jumeaux.
Brèves associées	>>> Premiers jumeaux		>>> Brèves – Premiers – Index
Pour en savoir plus	>>> Hypothèse de Riemann >>> Historique de la conjecture		>>> Conjectures >>> Congruences

938. Permutation figurées
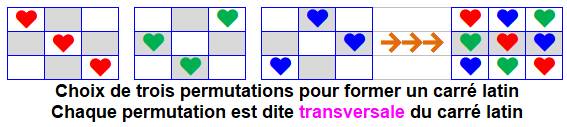
Une permutation peut être représentée par une certaine disposition sur un carré, comme ceci pour trois éléments: Ces permutations sont telles qu'un cœur ne se retrouve que sur une seule ligne et une seule colonne, et toutes les possibilités sont représentées. Ce sont ces dispositions transversales qui sont utilisées pour réaliser un carré latin. Exemple Elles ont été introduites en 1883 par le mathématicien Édouard Lucas, suite à ses études sur les motifs des tissus.
Brèves associées	>>> Permutations alternées	>>> Brèves – Compter – Index
Pour en savoir plus	>>> Permutations >>> Carrés latins	>>> Édouard Lucas

939. Motifs des tissus
Il existe trois types de motifs caractéristiques de tissage appelés armures: toile, sergé et satin. Ces armures peuvent être représentés par un quadrillage où les points de liaison entre fils sont signalés par un carré grisé. Ces points de liaison, pas plus de un par ligne et par colonne, forment des permutations figurées. Curieusement, à partir de ces motifs, les mathématiciens ont développé une géométrie discrète et même, du fait de la manipulation de nombres entiers, une confirmation de certains théorèmes de la théorie des nombres.		Toile Sergé Satin
Brèves associées	>>> Premiers jumeaux		>>> Brèves – Sciences – Index
Pour en savoir plus	>>> Géométrie des tisus		>>> Carrés latins

Retour	Brèves de maths – Page 46
Suite	Brèves de maths – Page 48
Voir	Voir liens en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve47.htm