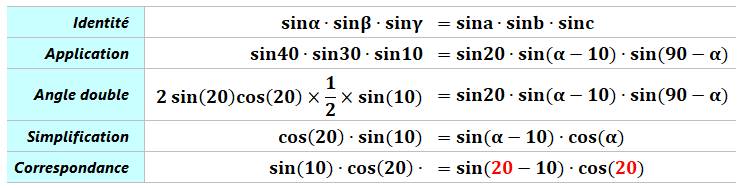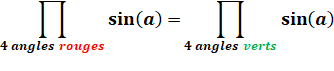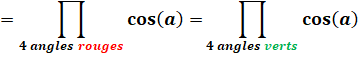Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 15/02/2024 M'écrire Brèves de Maths

INDEX Types de triangles Triangle Géométrie Défis en géométrie	Triangle: Droites remarquables
	Droites et points	Bissectrices	Médianes – Propriétés
	Point Milieu	Médiatrices	Médianes – Démo
	Point et triangles	Hauteurs	Médianes – Démo vecteurs
	Distances	Triangle médian	Médianes – Démo autres
	Théorème des céviennes		Céviennes régulières

Théorème des angles des céviennes Théorème remarquable conjuguant les sinus des angles trois par trois. Application à une énigme qui, sans ce théorème, est très difficile à résoudre.
	Sommaire de cette page >>> Théorème des angles des céviennes >>> Énigme – Deux solutions >>> Cas du rectangle >>> Cas du polygone régulier	Débutants Géométrie Glossaire Médianes Triangle

Voir Propriétés fondamentales des triangles

Théorème des angles des céviennes		haut
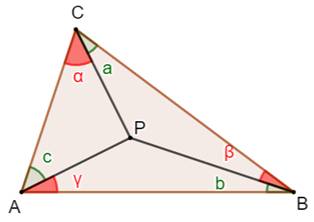
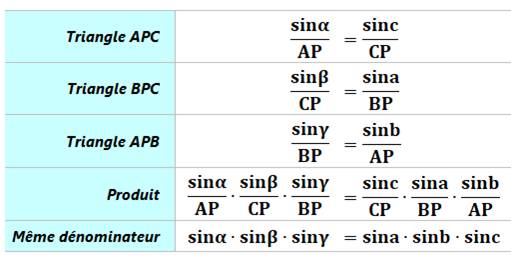
Triangle et céviennes Un triangle quelconque et un point P. Les trois céviennes AP, BP et CP. On identifie les six angles ainsi formés avec ces céviennes. Propriété Démonstration Application de la loi des sinus dans chacun des trois triangles internes.	Produit sinus rouges = produit sinus verts.

Voir Brève 57-1139

Énigme de l'angle		haut
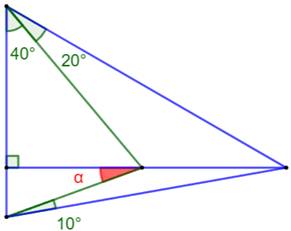
Construction Un triangle et une de ses hauteurs. Un cévienne qui divise l'angle en 40° et 20°. Une autre qui relie un sommet au point de concours des deux précédentes céviennes. On note un angle à 10°. Quelle est la valeur de l'angle alpha ?
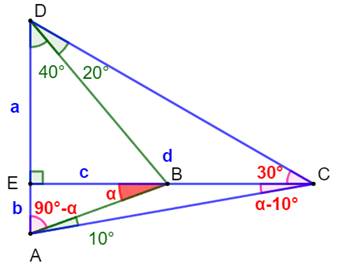
Piste Complétons la liste des angles connus: En D: 40° et 20° En C: 30° car le complément à 90° de 40°+20°. En A: 10° et 90°-α car le complément de α. Application du théorème des angles des céviennes et le résultat est immédiat.
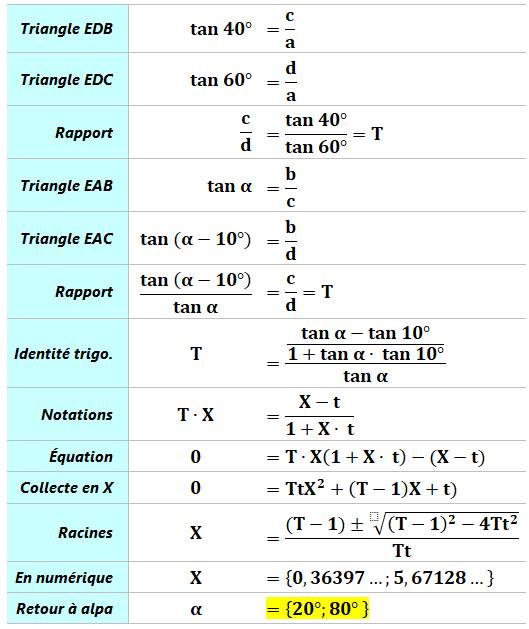
Calculs
Autre solution en passant par les tangentes des angles

Voir Identités trigonométriques / Équation du deuxième degré

Cas du rectangle		haut
Propriété (Ce symbole Pi majuscule signifie produit)
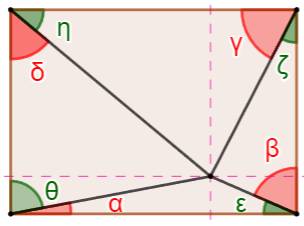
Démonstration La démonstration est du même ordre que celle pour le triangle. On s'appuie sur les segments figurant en pointillés. L'égalité avec les cosinus résulte du fait que chaque couple rouge + vert fait un angle de 90°, et sin (90° - a) = cos (a).	Commentaires Propriété valable pour le rectangle, mais pas pour un quadrilatère quelconque.

Cas du polygone régulier		haut
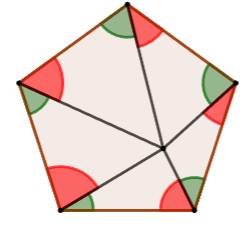
Propriété pour tout polygone régulier Démonstration La preuve est toujours basée sur le fait que, dans un triangle élémentaire, une des hauteurs est commune à un angle rouge et à un angle vert. En faisant le tour, chaque hauteur est impliquée pour un angle vert et pour un angle rouge.	Exemple du pentagone

Haut de page

Retour	Droites et points Céviennes régulières
Suite	Médianes concourantes – Démonstrations Illustration en 3D du centre de gravité d'un triangle Défis en géométrie – Index Construire le triangle connaissant les médianes Quatre triangles Triangles et carrés Triangles et droites de partage Triangle médian
Voir	DicoMot DicoNombre Droite de Simson Droite d'Euler Éléments de géométrie	Triangle – Débutants, novices Médianes – Glossaire Triangle – Index Cercle Losange et son cercle inscrit
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Propriet/CeviTheo.htm

Haut de page