Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 23/01/2024 M'écrire Brèves de Maths

INDEX Géométrie Énigmes Défis viraux Jeux et énigmes	Problèmes – Défis
	INDEX	Angles et cercle	Deux demi-cercles
	Nappe sur table	Quatre cercles et carré	Carré en 8, 10
	Carré oblique	Carré et triangle équil.	Défis divers
	Cercle et demi-cercle	Trois cercles tangents	Triangles dans triangle
	Triangle dans carré	Carré divisé

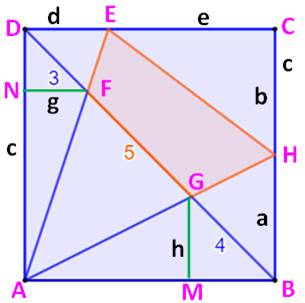
Carré divisé Un carré est divisé par une diagonale et deux sécantes. Retrouver l'aire de chacune des parties du carré. Notamment l'aire du quadrilatère intérieur. Ce défi n'est pas très compliqué, mais nécessite de la méthode.
	Sommaire de cette page >>> Le carré divisé	Débutants Géométrie Glossaire Géométrie

Le carré divisé		haut
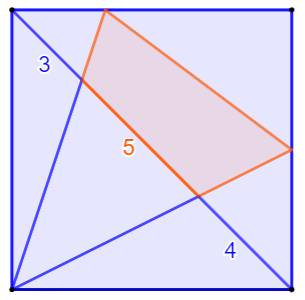
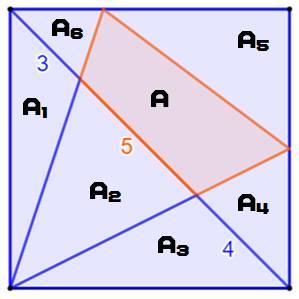
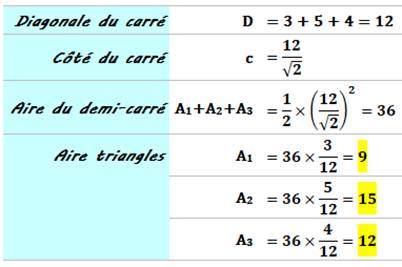
Construction Un carré est divisé en deux par une de ses diagonales. Puis par deux sécantes issues du même sommet et coupant la diagonale dans la proportion 3, 5, 4. Se présente un quadrilatère qui a pour sommets les points d'intersection avec la diagonale et les côtés du carré. Aires des six triangles et du quadrilatère ainsi formés ? Pistes On connait la diagonale du carré (3 + 5 + 4 = 12); on connait alors son côté. Les trois triangles ayant un sommet commun ont des aires proportionnelles aux longueurs des segments découpés. En effet, la hauteur est commune. Enfin, on mettra à profit le théorème de Thalès pour connaitre les longueurs des segments découpés sur les côtés du carré.
Aires des trois triangles de même sommet

Voir Brève 57-1126

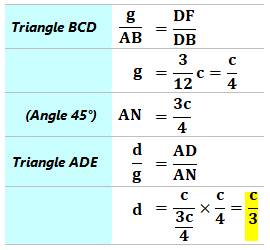
Découpe sur les côtés du carré On trace les perpendiculaires vertes. On met en évidence des proportions:

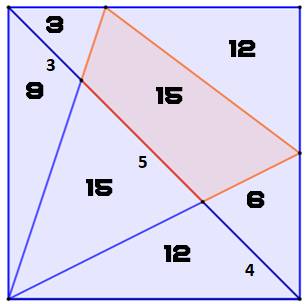
Calcul des aires

On connait les côtés de l'angle droit de tous les triangles.

Bilan

Notez que toutes ces aires sont en nombres entiers et les unes multiples des autres.

Haut de page

Retour	Défis – Index Géométrie – Index Énigmes – Index Brèves – Index
Suite	Divers défis 02 Équation en x^4 Technique de base de l'algèbre Tracas classiques en algèbre
Voir	Équations Calculs avec radicaux
Cette page	http://villemin.gerard.free.fr/aExercic/Probleme/CarreDiv.htm