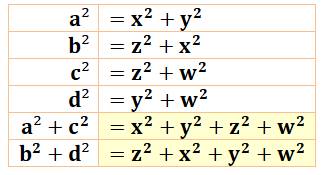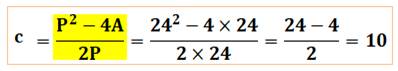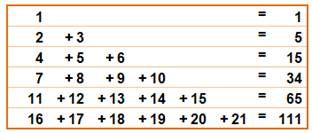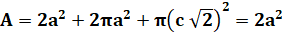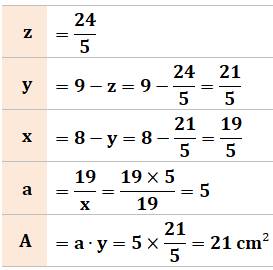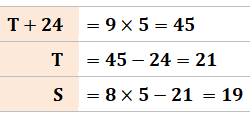|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
BRÈVES de MATHS – Page 56 Un millier de faits et chiffres sur les nombres et les
mathématiques
En principe ces pages sont très abordables sans
connaissances particulières de maths. Elles sont proposées dans un ordre
quelconque favorisant la découverte de sujets multiples. |
Anglais: Facts and figures about numbers and mathematics
1100. Nombres friables |
|
|||
|
Les nombres k-friables Ce sont les nombres dont les facteurs sont les
nombres premiers jusqu'à k uniquement. Les nombres 3-friables Ce sont les plus connus, les plus utilisés. Les facteurs sont 2 et 3 uniquement.
|
Exemples 1 024 = 210 est un nombre 2-friable
48 = 24 × 3 est un nombre
3-friable 10 800 = 24 × 33 × 52
est un nombre 5-friable Intérêt Notion
utile en théorie des nombres, notamment en cryptographie.
Inventée
par Leonard Adleman, co-inventeur du code RSA. |
|||
|
Brèves associées |
>>>
Nombre 5-friables >>> Tour de
Stockmeyer |
>>>
Brèves Types de nombres – Index |
||
|
Pour en savoir plus |
>>>
Nombres friables |
>>> Facteurs
spéciaux – Index |
||
1101. Tour de Stockmeyer |
|
|||
|
Présentation Similaire à la tour de Hanoï à quatre tiges, mais la quatrième est
centrale, et elle sert de pivot aux mouvements: une pièce ne peut être
déplacée que vers la tige centrale ou de la tige centrale vers une des trois
tiges périphériques. Quantité de mouvements La quantité minimale de mouvement pour k disques est la double-somme
des k plus petits nombres 3-friables. Soit vingt
mouvements pour quatre disques. |
Le jeu
Source
image: La tour de Stockmeyer
– Maths-en-Jeans |
|||
|
Brèves associées |
>>> Étoile cachée – Sam Lyod |
>>>
Brèves Jeux – Index |
||
|
Pour en savoir plus |
>>>
Tour de Stockmeyer >>>
Tour de Hanoï |
>>>
Nombres friables |
||
1102. Carrés des entiers |
|
|||
|
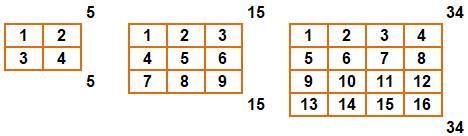
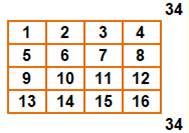
Méthode Les n² nombres entiers sont disposés en lignes puis en colonnes dans
une grille carrée de n cases par côtés. Somme sur les deux diagonales Elles sont égales. Elles valent: ½ n (n2 + 1)) |
Illustration pour n de 2 à 4 avec
sommes des deux diagonales
Pour 34, la somme vaut: ½ 4 (4² + 1) = ½ 4×17 =
34 |
|||
|
Brèves associées |
>>> Carré
magique avec dominos |
>>>
Brèves Grilles – Index |
||
|
Pour en savoir plus |
>>>
Carré des entiers |
>>>
Carrés magiques – Index |
||
1103. Triangles dans le pentagone |
|
|||
|
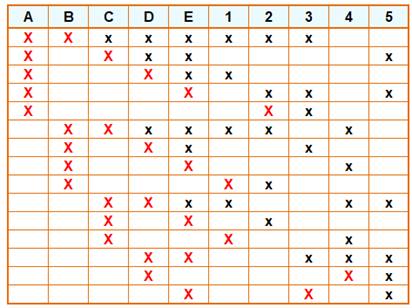
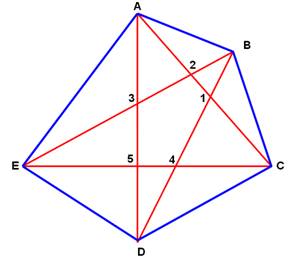
Décompte systématique des
triangles sur cette figure Deux croix rouges pour les sommets d'un segment. Une croix noire pour le troisième sommet du triangle. On compte 35 triangles.
|
Un pentagone et ses diagonales Sur cette figure on compte
35 triangles
|
|||
|
Brèves associées |
>>>
Triangles dans le triangle |
>>>
Brèves Dénombrement – Index |
||
|
Pour en savoir plus |
>>>
Triangles dans le pentagone |
>>>
Quadrilatère et ses diagonales |
||
1104. Rectangles imbriqués |
|
|||
|
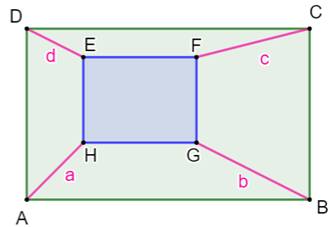
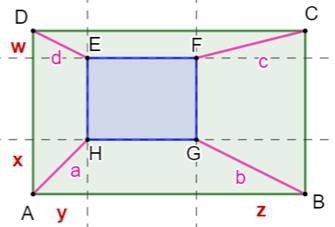
Construction Deux rectangles l'un dans l'autre et avec côtés
paralléles deux à deux. Propriété a² + c² = b² + d² Démonstration (Figure du bas) Avec le théorème de Pythagore:
|
|
|||
|
Brèves associées |
>>>
Rectangle en carré – Dissection |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Rectangles |
>>>
Théorème de Pythagore >>>
Défis en géométrie |
||
1105. Triangle rectangle, aire et périmètre |
|
|||
|
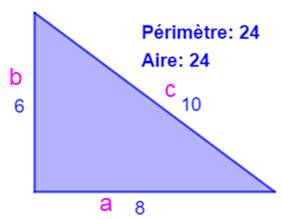
Construction Un triangle rectangle. Son aire est 24 et son
périmètre est aussi 24. Retrouver la longueur de chacun des trois côtés. Piste Nous disposons de trois équations: Avec trois équations il est possible de calculer
les trois inconnues a, b et c. Résultat pour l'hypoténuse c
|
|
|||
|
Brèves associées |
>>>
Triangle rectangle – Hauteur |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Détail du calcul de a, b et c |
>>>
Théorème de Pythagore >>>
Défis en géométrie |
||
1106. Pythagore & Einstein |
|
||
|
Deux formules importantes dans
l'histoire de l'humanité
|
|||
|
Brèves associées |
>>>
Fausse perspective |
>>>
Brèves Humour – Index |
|
|
Pour en savoir plus |
>>>
Pythagore >>>
Einstein |
>>>
Humour 2024 >>>
Pensées et humour |
|
1107. Somme magique |
|
|||
|
Somme magique du carré magique Un carré magique classique n×n est composé
des nombres de 1 à n² dont la somme vaut; Cette somme est répartie sur n lignes (ou n
colonnes). La somme magique vaut alors (en divisant par n): Ce qui donne la suite des nombres, à partir de n
= 3: Exemple: carré magique 4×4:
|
On retrouve souvent ces nombres Voyez ce tableau: Ou encore la somme de coefficients binomiaux
Ex: n = 5 =>
|
|||
|
Brèves associées |
>>> Carré
magique 3x3 |
>>>
Brèves Grilles – Index |
||
|
Pour en savoir plus |
>>>
Somme magique |
>>>
Somme des entiers >>>
Coefficients binomiaux |
||
1108. Énigme des verres empilés |
|
|||
|
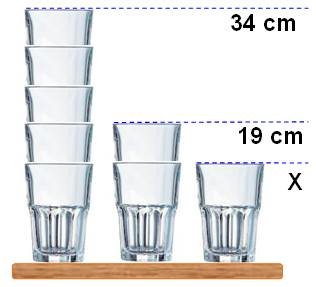
Énigme La hauteur de cinq verres empilés est 34 cm;
celle de deux verres est 19 cm. Quelle est la hauteur d'un verre ? Méthode à l'ancienne, mais simple
et efficace La différence 34 – 19 = 15 représente 3 fois la
contribution d'un verre. Une contribution mesure 15/3 = 5 cm. Celle-ci retirée de 19 cm donne la hauteur du
verre: Méthode algébrique
|
Verres empilés
|
|||
|
Brèves associées |
>>> Trois verres et dix pièces |
>>>
Brèves Énigme – Index |
||
|
Pour en savoir plus |
>>>
Énigme du verre penché |
>>>
Jeux et énigmes – Index |
||
1109. Nombres de Dedekind |
|
|||
|
Nombres de Dedekind Ces nombres servent à compter des objets
mathématiques un peu complexes comme les fonctions booléennes monotones. Découverts en 1897 par Richard Dedekind qui identifia
les cinq premiers nombres: 2, 3, 6, 20 et 7 581. En 2023, on a atteint le neuvième nombre qui
compte 42 chiffres. |
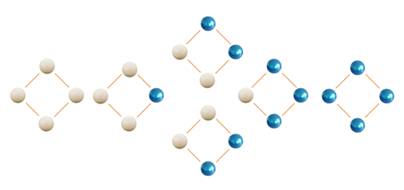
Exemple avec n = 2 avec le dessin
du carré
Il existe six façons de disposer les billes
blanches sans trouver une bille bleue plus à gauche qu'une blanche. Le troisième nombre de Dedekind est 6. |
|||
|
Brèves associées |
>>>
Nombres de Dudeney |
>>>
Brèves Types de nombres – Index |
||
|
Pour en savoir plus |
>>>
Nombres de Dedekind |
>>>
Dedekind et contemporains |
||
1110. Nombres divisibles par 4 |
|
|||
|
Théorème Tous les multiples de 4 (sauf 4) sont, au moins
une fois, différence de deux carrés. Les autres nombres pairs ne sont jamais différence de deux carrés. Méthode Il suffit de considérer un des produits de deux nombres pairs (a٠b) et d'appliquer une identité remarquable: |
Record de présentations: cas 1, 2 et 3
Exemple de calcul avec cas n°4 – Nombre 96
|
|||
|
Brèves associées |
>>> Somme
de puissances >>> Nombres
différence de carrés |
>>>
Brèves Puissances – Index |
||
|
Pour en savoir plus |
>>>
Différence de carrés >>>
Identité remarquable |
>>>
Nombre 96 >>>
Nombre 4 |
||
1111. Lunules et carré |
|
|||
|
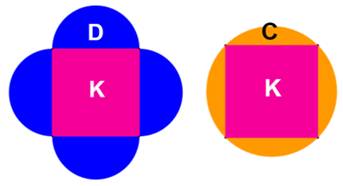
Construction Un carré et son cercle circonscrit. Quatre demi-cercles posés sur chacun des côtés du cercle. Quelle est l'aire de la zone colorée en bleu ?
Pistes Comment décomposer la figure de façon à simplifier les calculs ? Solution Figure en bas à gauche Prenons le carré et les demi-cercles (K + D), lesquels couvrent toute
la surface. Il faut retirer les zones blanches. Figure en bas à droite Prenons le cercle et le carré. La zone à éliminer est ici en orange et
sa surface vaut (C – K). L'aire de la zone bleue vaut: Si a est le côté du carré:
|
Les quatre lunules bleues ont la même surface que le carré. |
|||
|
Brèves associées |
>>> Pions en cercle |
>>>
Brèves Énigmes – Index |
||
|
Pour en savoir plus |
>>>
Lunules |
>>>
Défis géométriques – Index |
||
1112. Nombres 30 240 & 40 320 |
|
|||
|
Deux nombres avec les mêmes chiffres 30 240 = 25
× 33 × 5 × 7 40 320 = 27
× 32 × 5 × 7 Ils partagent les mêmes facteurs. Curieusement, ces deux nombres ont également la même quantité de
diviseurs. |
Quantité de diviseurs (fonction notée: tau) Cette quantité se calcule facilement en connaissant la factorisation
du nombre: C'est le produit de chacun des exposants augmenté de 1.
La même quantité résulte du fait que 6 × 4 = 8 × 3. |
|||
|
Brèves associées |
>>>
Nombre de Carroll |
>>>
Brèves Nombres – Index |
||
|
Pour en savoir plus |
>>>
Nombre 30 240 |
>>>
Quantité de diviseurs |
||
1113. Voyelles et nombres impairs |
|
|||
|
Énigme Ces quatre cartes comportent une lettre sur une
face et un nombre sur l'autre. Toute
carte avec une voyelle sur une face porte un nombre impair sur l'autre. Quelles cartes faut-il retourner pour vérifier
cette affirmation ? Piste (ou piège déjoué) On ne demande de vérifier que "voyelle-impair". Il n'est pas dit que
"consonne-pair" est obligatoire. Alors, inutile de vérifier B et 2. Solution Il suffit de retourner A et 1. |
Cartes présentées
Historique Peter Wason (1924-2003), un psychologue et son
collègue Johnson-Laird ont proposé ce casse-tête en 1966 à 128
universitaires. La majorité s'est trompée en choisissant la
confirmation de l'affirmation plutôt que sa négation. Tendance connue comme: biais de confirmation. |
|||
|
Brèves associées |
>>> Voitures sur parking |
>>>
Brèves Énigmes – Index |
||
|
Pour en savoir plus |
>>>
Voyelles et nombres impairs - Suite |
>>>
Logique – Index |
||
1114. Aire du rectangle ? |
|
|||
|
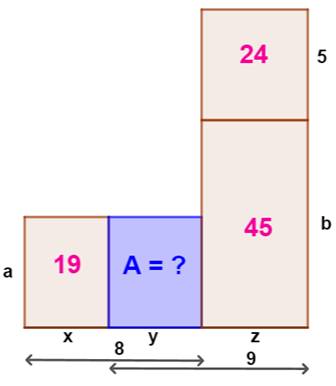
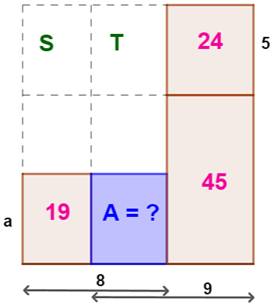
Problème Sur cette figure certains éléments sont connus. Retrouver l'aire du rectangle bleu. Solution Calcul des longueurs pas à pas:
Notez que l'aire 45
est purement indicative. La hauteur b peut être quelconque.
|
|
|||
|
Solution avec astuce Compléter la figure comme indiqué.
Le rectangle S a même aire (19) que celui du bas
et la même largeur; sa longueur est donc 5 cm. Le rectangle T aussi a une larguer égale à 5. Il
a la même largeur que le rectangle A. Donc: A = T = 21 cm². |
|
|||
|
Brèves associées |
>>> Aire
du rectangle dans le triangle |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Défis en géométrie – Index |
>>>
Calculs d'aires |
||
1115. Énigme du 4 donne 5 |
|
|||
|
Énigme Avec ces trois relations, dont la partie
intermédiaire est à découvrir, reconstituer la quatrième. Solution Prendre le carré du nombre et faire la soustraction des unités et des
dizaines. Ainsi: 4 devient 16 et 6 – 1 = 5; etc. Alors: 7 devient 49 et 9 – 4 =
5 La solution est 5. Ou comment 4567 devient 5335,
un palindrome. |
Données de l'énigme
|
|||
|
Brèves associées |
>>> Énigme des verres et du barman |
>>> Brèves
Énigmes – Index |
||
|
Pour en savoir plus |
>>>
Énigme du 4 donne 5 – Suite |
>>>
Énigmes virales sur le net |
||
1116. Carré dans quart de cercle |
|
|||
|
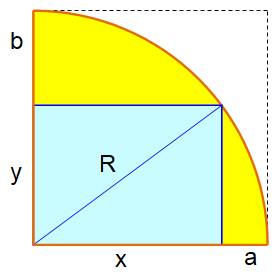
Énigme Sur cette figure, on donne les mesures a et b. Trouver la valeur du rayon du cercle en fonction
de a et de b. Piste Le théorème
de Pythagore et la résolution des équations
du deuxième degré suffiront. Calculs
|
Figure
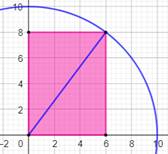
Application numérique Prenons a = 4 cm et b = 2 cm Alors R = 6 + 4 = 10
La solution R = 6 – 4 = 2
n'est pas retenue car alors R – a = 0 et R – b est négatif. |
|||
|
Brèves associées |
>>> Carré
dans le triangle rectangle |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Défis en géométrie – Simples |
>>>
Jeux et énigmes – Index |
||
1117. Nombre d'or et super doré |
|
||||||||||||
|
Les trois constantes Il existe
plusieurs constantes résultant de la convergence du ratio de deux nombres
successifs pris dans les suites de
À droite,
valeur et l'équation dont elles sont racines. Suite de Narayna Comme pour la suite de Fibonacci, on définit les
points de départ et la récurrence: A0 = 0; A1 = 1; A2
= 1; A3 = 1; AN+1 = AN-1 + AN-3 Nombres de la suite de Narayana 1, 1, 1, 2, 3, 4, 6, 9, 13, 19, 28, 41, 60, 88,
129, 189, 277, 406, 595, 872, 1278,…
et 1278/872 = 1,465… |
|
||||||||||||
|
Brèves associées |
>>>
Nombre d'or et nombre d'argent |
>>>
Brèves Nombres – Index |
|||||||||||
|
Pour en savoir plus |
>>>
Super nombre d'or |
>>>
Nombre d'or |
|||||||||||
1118. Coefficients du triangle de Pascal |
|
|||
|
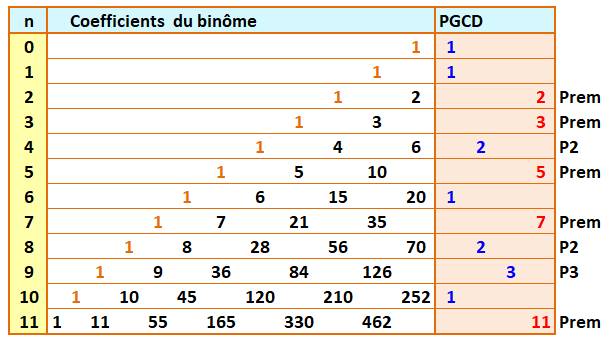
Le triangle de Pascal Seule la partie gauche du triangle est
représentée. La partie droite est symétrique. Pour chaque ligne, on calcule le PGCD des
nombres, sauf le 1 initial.
Observation Lorsque n est premier, le PGCD est égal à n si n
est premier. Il est égal a p si n est une puissance p. Il est égal à 1 dans
tous les autres cas. |
||||
|
Pourquoi ? Notez que si n est premier, les coefficients sont des multiples de n.
Car le n du numérateur n'est jamais divisible par les nombres au
dénominateur.
|
Exemple: coefficient n°4 de la
ligne 7
|
|||
|
Brèves associées |
>>>
Produit dans le triangle de Pascal |
>>>
Brèves Suites – Index |
||
|
Pour en savoir plus |
>>> Théorème
de divisibilité des coeff. |
>>>
Divisibilité par 7 |
||
1119. Nombre de Heesch |
|
|||
|
Pavage fini Un pavage consiste à couvrir le plan avec des
tuiles sans chevauchement et sans trou. Il existe une grande variété de pavages. Ici, on
s'intéresse au pavage fini. Le principe consiste à poser une tuile et, avec
le même type de tuile, à l'endroit ou à l'envers, à faire le tour de la
première. En fait, il s'agit de créer une sorte de couronne autour de la
première tuile. S'il est possible de créer cette couronne, sans
qu'il soit possible de créer une nouvelle couronne, le nombre de Heesch de la tuile est 1. Record En fin 2023, on sait créer des tuiles avec les nombres de Heesch
de 1 à 6. On ne sait pas si elles existent pour n = 7 et
au-delà. |
Tuile en forme d'un H allongé
Une couronne autour du H, mais on peut continuer.
Ce pavage est infini. Tuile en goutte d'eau: H = 1
Impossible de créer une nouvelle couronne. |
|||
|
Brèves associées |
>>> Réseaux – Chemin sur grille |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Pavage fini – Nombre de Heesch |
>>>
Pavages avec polygones |
||
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()