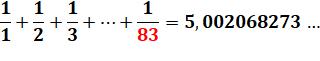collection de nombres, suite harmonique

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 02/11/2021 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Suites & Séries
Débutants Général	CLASSIQUES			Glossaire Suites
INDEX Suites	Général	Harmonique	Suite aliquote
	Harmonique déguisée	Harmonique pondérée	Chiffres disparus
	Typiques	De Farey	Séquences numériques
	1 / (1 - x)	De Martin-Löf	Thue Morse
	x^k / (x^k – 1)	Engel	Kempner
	1 – 1 + 1 – 1 + …	de l'artiste	Inverses premiers
		Sommaire de cette page >>> Nombres harmoniques >>> Série harmonique et voisines >>> Autres séries cousines >>> Suite harmonique – Limite >>> Calcul & comparaison à "C" (Euler) >>> Progression selon n entier >>> Suite harmonique du 2^e ordre >>> Suite harmonique du 3^e ordre >>> Suite harmonique du N^ième ordre >>> Curiosité avec e

SÉRIE HARMONIQUE

& autres séries voisines

Des termes de plus en plus petits qui finissent par former l'infini, ou non! La plus simple est appelée série harmonique.

Note

Les mots suite et série étaient utilisés l'un pour l'autre.

Aujourd'hui on réserve plutôt:

Suite : séquence de termes comme U_n , U_n+1 , …

Série : somme de termes comme 1 + 1/2 + 1/3 + …

Voir Achille et la tortue / Historique

Nombres harmoniques

Les nombres harmoniques sont la somme des inverses des nombres successifs de 1 à n.

Somme des fractions	Valeur
Somme des fractions	Fraction	Numérique
1/1	1	1
+ 1/2	3/2	1,5
+ 1/3	11/6	1,8 3 3 …
+ 1/4	25/12	2,08 3 3 …
+ 1/5	137/60	2,28 3 3 …
+ 1/6	49/20	2,45
+ 1/7	363/140	2,59 285714 285714 …
+ 1/8	761/280	2,717 857142 857142 …
+ 1/9	7129/2520	2,82896 825396 825396 …

Suite en Table des nombres harmoniques

Convergence

La suite est supérieure à une somme qui est manifestement croissante

Rappel
Montrez que ces sommes sont supérieures à ½.

Termes du numérateur minorés par 5.6.7

En généralisant

La somme des fractions de 1 / (2ⁿ + 1) à 1 / 2ⁿ⁺¹

est supérieure à 1/2.

Série harmonique et voisines
		>>> Série harmonique
		>>> Série alternée >>> Déguisement !
		>>> Impairs
		>>> Factorielles (NB départ avec 1/0! = 1)
		>>> Puissances de 2
		>>> Carrés
		>>> Kempner (sans 9)
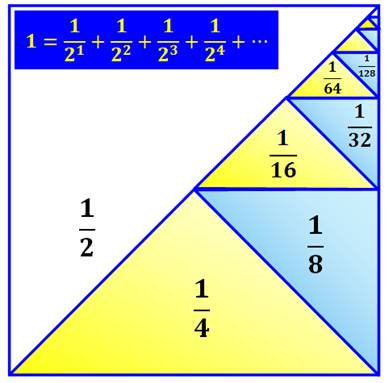
Calcul d'une progression géométrique de raison 1/2.	Somme des inverses des puissances de 2 Démonstration graphique

Cas de (1 – 1/k)

Série divergente

Exemple pour k = 1 000 000 alors S = 999985,6073…

Cas de (n+1) / n

Série divergente

Test de la divergence: si la limite du terme de la série n’est pas nulle ou elle n’existe pas, alors la somme diverge.

Ici la limite de (n+1)/n est 1 pour n infini, alors la série diverge. Test qui s’applique aussi la série ci-dessus.

Attention : si la limite est nulle, aucune conclusion possible. Par exemple 1/n vaut 0 pour infini et pourtant la suite harmonique diverge.

Cas de 1/k !

Série convergente avec l’inverse des factorielles

Voir Exponentielle

Calcul amusant

Prenons la série qui lui ressemble, mais avec les impairs au numérateur:

La même série divisée par 2:

La différence:

On reconnait la série initiale S.

T/2 = 1 + S

T = 2 + 2S = 6

Un calcul similaire

Au numérateur la suite de Fibonacci et

au dénominateur les puissances de 2.

Autres séries cousines
La somme des inverses des nombres premiers est divergente comme la série harmonique, mais encore moins vite.
H(n) Inverse des entiers (harmonique) Quand n tend vers l'infini, H(n) et ln n sont équivalentes. Le rapport des deux quantités tend vers 1. H(10 milliards) = 23	P(n) Inverse des premiers Quand n tend vers l'infini, H(n) et ln ln n sont équivalentes. C'est bien le log népérien de log n. P(10 milliards) = 3
Les suites suivantes convergent: la série des inverses des carrés 1/n². les séries harmoniques privées des nombres dont le développement décimal comporte un chiffre donné (le 3 ou le 9 ou …). Propriété prouvée en 1914 par A. Kemper. les séries harmoniques privées des nombres comportant un chiffre donné (le 3 ou le 9 ou …) au dénominateur. A fortiori par privation de plusieurs chiffres. Irwin (1916) >>> En 1995, Behforooz démontre sous quelles conditions de telles séries convergent.

Voir Série harmonique pondérée

Série harmonique – Limite

Cette suite est lentement divergente. Il faut 10⁴³⁴ termes pour atteindre la somme de 1 000.

Pour n infini, la série harmonique croît comme le logarithme népérien de n augmenté d'une constante, la constante gamma d'Euler.

Comparaison

La convergence vers un écart limité à gamma est très lente.

Pour une valeur donnée de n, la valeur approchée est donnée par un développement limité:

Exemple de calcul avec n = 10

Avec la connaissance du nième nombre premier, qui vaut approximativement n ln n, on peut calculer H_n sans à avoir à calculer le logarithme.

Exemple avec n = 60, sachant que le 60^e premier est 281.

p₆₀ = n ln n = 281

H₆₀ 0,577 + 281 / 60 = 5,26

Progression selon n entier
Valeur du dernier dénominateur (D) pour que la somme dépasse n entier. Exemple: (5 => 83)	Valeur de D pour les n successifs 1, 4, 11, 31, 83, 227, 616, 1 674, 4 550, 12 367, 33 617, 91 380, 248 397, 675 214, 1 835 421, 4 989 191, 13 562 027, 36 865 412, 100 210 581 …
Programme	Commentaires n commence avec 1: H est la somme de la série harmonique et L est la liste des valeurs successives de D. Boucle de recherche en n. Si la somme; S dépasse l'entier T, n est ajouté à la liste et T est incrémenté de 1. Fin de boucle et impression de la liste. En bleu, résultat du traitement.