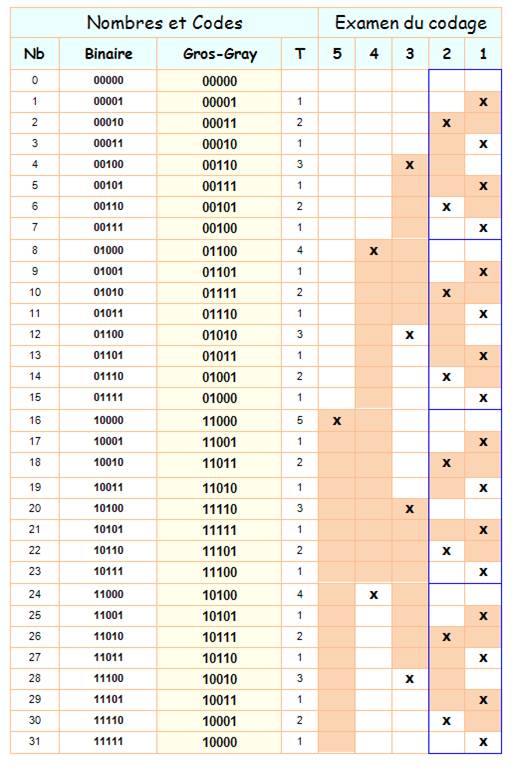
code Gros Gray, codage binaire, baguenaudier,hanoi

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 19/04/2017 Orientation générale DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	NUMÉRATION
Débutants Binaire	BINAIRE			Glossaire Général
Index des pages NUMÉRATION >>> INDEX	Débutants	Introduction	Conversion
	Magie	Informatique	Table 512
	Code Gray	Numérique
		Tour de Hanoi	Baguenaudier
		Sommaire de cette page >>> Code Gros-Gray >>> Tableau de codage >>> Bit de transition >>> Compter avec le code Gray >>> Généralisation du code Gros-Gray >>> Dérivée du code Gray et binaire pur

Code GROS-GRAY

Plus connu sous le nom de code Gray.

Ce code binaire possède une particularité unique: le passage au nombre suivant n'engendre le changement que d'un seul chiffre.

Il n'y a jamais de basculement de plusieurs digits à la fois comme, par exemple en décimal, lors du passage de 999 à 1000.

CODE GROS-GRAY

Le codage Gros-Gray est utile pour

Résoudre les problèmes et énigmes telles que:

baguenaudier et spin-out,

tour de Hanoi,

problème du voyageur de commerce,

etc.

Traiter des problèmes plus théoriques comme:

les pistes de codage sur encodeurs mécaniques ou optoélectroniques,

l'exploitation des ordinateurs parallèles,

l'optimisation des communications,

etc.

Principe

Codage dont, seul un digit change, pour passer au nombre suivant.

Il s'agit d'éviter le passage en bloc du type 999 à 1000, par exemple; ou plutôt, de 111 à 1000 en binaire.

En code Gros-Gray, après 111, on trouve 101, seul le bit central a changé.

Historique

Louis Gros était clerc de notaire à Lyon. Il publia en 1872 un document donnant la solution de casse-tête et ce code y était mentionné.

Frank Gray travaillait aux laboratoires Bell. Il réinventa le code et publia son étude en 1930.

Tableau de codage Gros-Gray

Notations

X = changement de valeur

T = taille ou hauteur du premier 1

Orange: bit à 1

Blanc: bit à 0

Valeurs

FRACTALE

La progression du code (marquage orange) donne un air de fractale au codage Gros-Gray: des motifs à petite échelle qui se répètent à grande échelle.

De fait, le parcours du voyageur de commerce est d'allure fractale.

Avec un parallélépipède dont les côtés seraient de longueur 1/2ⁿ, le trajet serait effectivement de nature fractale.

BIT de transition

Examen du codage

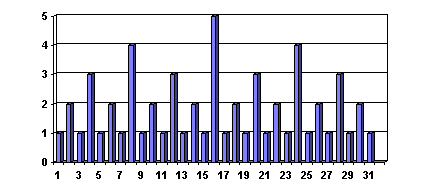
Les colonnes 1, 2, 3, 4 et 5 montrent quand le bit correspondant est à 1 et indiquent les transitions de 0 à 1 et de 1 à 0.

La colonne T le numéro (hauteur) du bit qui change, le numéro de transition.

Numéro de transition

Sa formation par récurrence est simple.

Lorsqu'on connaît un morceau de la séquence, on la recopie à la suite et on ajoute 1 au dernier nombre.

Le premier morceau de la séquence est 1.

Soit

*Numéro Transition*	*Recopie + 1*
1
1	2
12	13
1213	1214
1213 1214	1213 1215
1213 1214 1213 1215	1213 1214 1213 1216

Illustration

Cette suite de nombre est appelée: la suite de la copie augmentée.

Compter en Gros-Gray

Compter

On passe d'un nombre au suivant en changeant un bit:

Règle 1: le dernier si le nombre de " 1 " est pair, et

Règle 2: celui à gauche du " 1 " le plus à droite, sinon.

Exemple:

Progression en Gros-Gray

Pour passer des 2n premiers aux 2n suivants, on recopie les codes des premiers à l'envers et on fait précéder d'un " 1 ".

*Exemple*	0	1	2	3	4	5	6	7
Connus	00	01	11	10
Copie à l'envers					10	11	01	00
Avec 1 en tête					110	111	101	100

GÉNÉRALISATION DU CODE GROS-GRAY
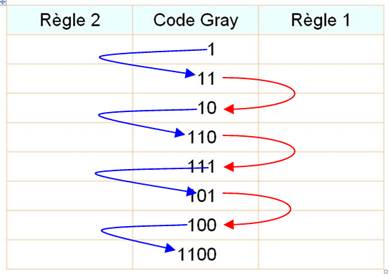
Le motif du dernier bit est => Celui du deuxième=> Pour le ième =>	0 1 1 0 0 1 1 0 0 1 1 1 1 0 0 0 0 2ⁱ fois " 0 ", puis 2ⁱ⁺¹ le " 1 ", 2ⁱ⁺¹ le " 0 ", etc.
Avec cette règle, on peut généraliser à d'autres bases: En base 3 le dernier digit sera: 0122100122100... l'avant dernier sera: 000111222222111000000111...

Dérivée, ou passage du binaire au Gray

En dérivant le code binaire d'un nombre, on obtient son codage Gros-Gray.

Le premier bit est 1 dans les deux codes.

Le bit i (en partant de la gauche) = 0, si les i-1 et i du binaire sont égaux.

Il est = 1 dans les autres cas.

Exemple:

	*Premier bit*	*Suivants*
14 = 1110		11	11	10
Code GG	1	0	0	1	=> 1001

Note personnelle

Il y a quelques dizaines d'années déjà, en tant qu'ingénieur électronicien, je concevais des systèmes comportant des capteurs de position angulaire munis de codeurs Gros-Gray. Le codeur comportait, par exemple, 10 pistes pour coder des nombres en binaire à 10 bits. Avec ces 10 bits, le codeur permet de repérer 2¹⁰ = 1 024 positions angulaires sur un tour. En tournant, le codeur transmet l'état de ses pistes au moyen d'un balai qui fait contact ou d'un capteur photoélectrique. L'avantage du code Gros-Gray se manifeste ici: un seul signal sur les dix émis change à la fois. les risques d'erreurs de transmission sont moindres et il est même possible de contrôler la règle de la transition unitaire.