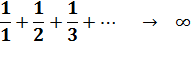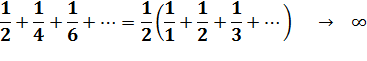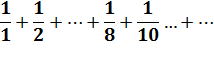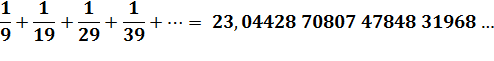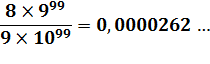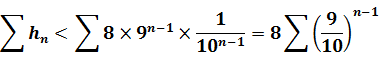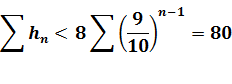|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
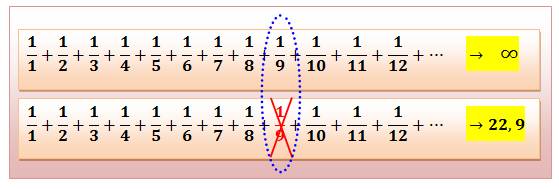
SÉRIE de KEMPNER Série d'IRWIN La série
harmonique est divergente. Est-il possible de la transformer pour la
rendre convergente? Oui! En lui retirant tous les termes comprenant un nombre
donné. Un 9, par exemple. Surprenant, non?
|
Anglais: Summing Kempner's Curious (Slowly-Convergent) Series
|
|
||
|
Suite harmonique Elle
diverge. |
|
|
|
Essayons un sur deux? Elle
diverge toujours. |
|
|
|
En supprimant certains termes? Sans les
dénominateurs avec 9, elle converge. C'est la suite
de Kempner. |
Les fractions 1/9, 1/19, 1/29 … ont été retirées. |
|
|
En conservant ces termes C'est la suite d'Irwin avec un 9 seulement au
dénominateur (99 est exclu). |
|
|
|
Somme des deux |
La somme des deux séries de Kempner
et Irwin n'est pas la série harmonique. Les doublons font la différence. Ex:
1/99 est éliminé de Kempner comme d'Irwin. |
|
|
|
||
|
Convergence |
Aubrey J. Kempner (1880-1973)
a prouvé (1914) que la somme converge vers une valeur
inférieure à 80. Depuis, on a aussi prouvé que la suite converge dès
qu'on lui retire les fractions avec un chiffre quelconque ou, même, un nombre
quelconque. Intuitivement, plus un nombre est grand plus la
probabilité de contenir au moins un 9 augmente. Par exemple, avec 100
chiffres, 99,99997% des fractions sont éliminées. Un graphe montrant les nombres retenus et non retenus
présente une structure fractale. |
|
|
Calcul de convergence |
La convergence est si lente que le calcul classique de
la somme montrant la convergence est impossible. Avec 10 millions de termes,
la somme est encore à 14 au lieu de 22,9… La somme atteint 22 pour 1028
termes. Il faut recourir à des algorithmes
plus sophistiqués pour prouver la convergence. En 2008, Thomas Schmelzer et
Robert Baillie développent un tel algorithme. Les valeurs
indiquées ci-dessous on été calculées avec ce logiciel. |
|
|
|
||
|
Termes retirés |
De 1 à 9: 1 (un seul terme avec 9 à éliminer;
c'est 1/9). De 10 à 99: 8 x 1 + 10 = 18 (Ce sont: 19, 29, 39,…90, 91, …99) De 100 à 999: 8 x1 + 8 x 18 + 10² = 252 NB. il s'agit bien des termes comportant au
moins un 9. Par exemple 99, ne compte que pour 1. Dit-autrement: il y a bien 20 fois le chiffre 9 dans les
nombres de 1 à 99, mais seulement 19 termes à éliminer. Considérons la suite de la quantité des nombres
restants: 8,
72, 648, 5 832 … Notez que c'est: 8 x 1, 8 x 9,
8 x 81, 8 x
729 … La quantité des nombres retenus est égale à: De 10n à 10n+1 : 8 x 9n Exemple: jusqu'à 100
chiffres, n = 99 et la fraction de nombres conservés est:
|
|
|
Terme majoré |
De
10n à 10n+1 le plus grand terme est 1/10n |
|
|
Borne supérieure |
Si
tous les termes non éliminés valaient le plus grand terme nous aurions une
valeur supérieure à la somme réelle de ces valeurs:
|
|
|
Progression géométrique |
La somme est bornée
par 80. |
|
|
Théorème de Kempner (1914) La
somme de la série de Kempner est convergente: série
harmonique privée des termes comportant un nombre particulier. La somme de
plusieurs telles séries est convergente. Théorème d'Irwin (1916) La
somme de la série d'Irwin est convergente: série du type harmonique ne comportant que des termes avec un nombre
particulier et, en un seul exemplaire. |
Quelques résultats de convergence
Notes: 9 unique: indique que le terme éliminé
comporte exactement un 9, pas plus (Irwin). Pas de pairs: signifie
que, parmi les chiffres du dénominateur, aucun n'est pair. |
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
![]()