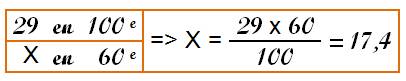NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 26/03/2020 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Numération
Débutants Décimal	BASES						Glossaire Nombres
INDEX Numération	B2	B8	B12	B10	B16	B20		B60
			Sommaire de cette page >>> Nombres en base 60 >>> Fortement composé >>> Usage de la base 60 >>> Calcul en minutes et secondes >>> Conversion degrés

Base de numération

sexagésimale (60)

La base soixante a été bien utilisée par nos ancêtres et nous l'utilisons toujours pour compter les minutes et les secondes ou les angles en degrés.

Anglais: Sexagesimal number system or sexagesimal counting system or base-60 notational system

Nombres en base 60
En base 60, chaque "chiffre" vaut une puissance de 60. En base 60, il y a 60 "chiffres": {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, …}. Jamais utilisé. Les logiciels utilisent les nombres décimaux. Et même, le plus souvent, dans l'ordre inverse, comme avec le logiciel Mapple.	12360 = 1 x 60^2 + 2 x 60^1 + 3 x 60^0 = 3 600 + 120 + 3 = 3 723 en décimal 1AJ60 = [1, 10, 19] 1AJ20 = [19, 10 , 1]Mapple

Le nombre 60 est fortement composé

	60 = 1 x 2² x 3 x 5
Diviseurs	1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
Quantité	12
Somme	168

Le nombre 60 comporte 12 diviseurs. Il est fortement composé. Il est divisible par tous les nombres jusqu'à 6. Ce qui explique son choix comme base de numération. Avec lui, il est possible de former de nombreuses fractions pratiques pour un usage dans la vie de tous les jours.

Base 60 – Usage

Pourquoi 60 Le nombre 60 a de nombreux diviseurs: {2,3,4,5,6,10,12,15,20,30}. C'est même le plus petit nombre divisible par 1, 2, 3, 4 et 5. Ce nombres est de ce fait bien pratique pour les divisions, les fractions. Sexagésimal vient du latin sexaginta, soixante. Mésopotamiens Vers 3000 av. J.-C. les Chaldéens (Chaldée: région de Sumer en Mésopotamie / Babylone / Irak). avaient adopté la base 60 car, selon eux, 1 an est divisé en 6 périodes de 60 jours (360 jours). Et, en astronomie, ils utilisaient un degré de 60 minutes et une minute de 60 secondes. Les Anciens avaient constaté que le Soleil retrouvait sa place par rapport aux étoiles après douze lunaisons (3 saisons de 4 mois de 30 jours), soit 360 jours. Les calendriers étaient lunaires, car l'observation était facile. >>> Pour les Babyloniens 10 00060 = 12 960 00010 désignait un nombre très grand et souvent indéterminé. >>> Ce système de comptage est un système de numération de position sans zéro. Un espace remplaçait le zéro; puis vint un symbole fait de deux coins. Il l'utilisait essentiellement pour noter les transactions financières. Plus précisément: Les Babyloniens comptaient en base 10 jusqu'à 60: on écrivait 32 avec trois signes cunéiformes valant 10 puis deux valant 1. À partir de 60, il introduisant un nouveau signe: on écrivait 131 avec deux signes 60, un signe 10 et un signe1. Voir Historique minutes et secondes Arabes Les Arabes ont utilisé ce système. Pour témoignage, vers1400, Al-Kashi un astronome arabe, calcule aussi bien en décimal qu'en sexagésimal. Voir Valeurs de Pi En Latin Fractiones vulgares était utilisé pour désigner les fractions décimales des fractions sexagésimales. Aujourd'hui Mesure du temps avec les heures, minutes et les secondes. Système (24, 60,60). Ex: 7h 15min 8s = 7x 60² + 15 x 60 + 8 = 26 108 s Mesure des angles avec les degrés, minutes et secondes. Système (360, 60,60). Utilisé notamment en: Trigonométrie Géographie: indications des coordonnées: latitude et longitude. Remarques: lorsque le confusion est possible avec les durées, on ajoute minute d'arc et secondes d'arc. Après les secondes, on donne les fractions décimales de seconde (dixième, centièmes … de seconde). La tierce valant un soixantième de seconde n'est pas utilisée.

Calcul des minutes et secondes de temps
Addition Additions et soustractions s'effectuent comme d'habitude. Secondes avec secondes; minutes avec minutes et heures avec heures. Tout "paquet" de 60 secondes devient une minute; et tout "paquet" de 60 minutes devient une heure. Une retenue spéciale tout les 60 en quelque sorte. Multiplication Mon travail dure 1h 20 min et 30 s. Je dois le réaliser 5 fois. Combine de temps cela durera-t-il? Le même principe s'applique pour une multiplication d'une durée par un nombre entier. Je multiplie séparément les heures, minutes et secondes et je reporte les "paquets" de 60 secondes en minutes et ceux de minutes en heures. Pour me rassurer, je peux convertir la durée en secondes. Je multiplie le nombre de secondes par 5 puis je reviens en heures et minutes: Je divise la quantité de secondes par 60. Le quotient donne les minutes et le reste les secondes; puis Je divise la quantité de minutes par 60. Le quotient donne les heures et le reste les minutes.

Conversion des degrés, minutes et secondes d'angle

Il est fréquent de connaître un angle en degrés décimaux. Comment convertir en degrés sexagésimaux? Ex: un cercle est divisé par 7. Quel est la valeur de l'angle au centre? Conversion des degrés en secondes en multipliant par 3 600. Division de ce nombre par 7 Conversion de ces secondes en minute et degrés comme ci-dessus. Résultat 360° / 7 = 51° 25' 42,85…" Notez que le ",85" s'applique aux secondes, soit 85 centièmes de seconde. On pourrait convertir celles-ci en soixantièmes d'une nouvelle unité venant après les secondes, les tierces. Ce serait 0,85 x 60 = 51 tierces. En degrés décimaux, 1 radian = 57, 29577951 30823208 … Je conserve les degrés et je convertis les décimales 0,29…° à convertir en X minutes ou soixantièmes de degrés. X = 0,29.. x 60 = 17,74… minutes. Je conserve les minutes et je convertis les décimales 0,74…' à convertir en Y secondes ou soixantièmes de minutes. Y = 0,74.. x 60 = 44,80… secondes. Résultat: 1 radian = 57° 17' 44" et 0,80… seconde Truc: Il faut multiplier ou diviser par 60? Avec cet exemple: 57,29 …° nous avons 29 centièmes de degrés soit un peu plus du quart et moins que le tiers de 100 centièmes. En minutes, nous devrons trouver la même proportion de 60 minutes, soit une valeur entre 60/4 = 15 et 60/3 = 20. Nous avons trouvé 17,7. C'est bon! Sinon appliquez la règle de trois: si nous avons 29 en centièmes, combien aurons-nous en soixantièmes. Le résultat X est le produit en croix:

Suite	Année Voir index en haut de page
Voir	Nombres Numération
DicoNombre	Nombre 60
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Numerati/aaaBASE/B60.htm