nombre 12 et douzaine

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 05/02/2022 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	RUBRIQUE Nombres
Débutants Général	Nom particulier				Glossaire Général
	Nombre 12	Douzaine	Base 60	Nombre 16
		Sommaire de cette page >>> Douzaine >>> Base 12 >>> Commentaires >>> Ah, si nous avions tous douze doigts! >>> Table des nombres de 1 à 100 en duodécimal >>> Anglais

Nombre 12 – Douzaine

Système de numération à base 12: duodécimal

La base de numération duodécimale s'est faufilée dans la vie courante sans réussir à s'imposer, mais y a laissé des vestiges. Pourquoi, parce que les base 12 ou 12x12 ou même 12 x 20 étaient plus pratiques pour faire des partages. Beaucoup moins commodes pour les conversions … lorsqu'on compte en base 10.

Les œufs sont toujours vendus

par douzaines

(ou six ou dix)

Anglais:

Eggs are sold by the dozen

Relatif à douze

Dodécuple, dodécupler

Douzaine

Douze

Douzième

Douzièmement

Duodécimain

Duodécimal

Note: duodénum, duodénal => relatif à la portion initiale de l'intestin grêle. Du latin duodenum digitorum: douze doigts.

Dodécaédrique

Dodécagonal

Dodécagone

Dodécane (C₁₂H₂₆)

Dodécanèse (archipel grec)

Dodécaphonique (12 sons)

Dodécastyle (rang de 12 colonnes comme le Palais Bourbon).

Dodécasyllabe

Dodecatheon (fleur)

DOUZAINE
6	Une demi-douzaine (half a dozen)	>>>
12	Une douzaine (dozen)	>>>
13	Treize à la douzaine (long dozen or baker's dozen)	>>>
10 x 12 = 120	Grande centaine, ou Petite grosse (small gross or short gross)	>>>
12 x 12 = 144	Grosse (gross)	>>>
12 x 144 = 1728	Grande grosse (great gross)	>>>

BASE 12 – Avantages
Douzaine signifie 12. Parfois douzaine désigne une quantité approchant 12, comme une vingtaine ou une centaine. Le système à base 12 (duodécimal ou dozénal) Notre base 10 a quelques désavantages: une simple division par 3 pose problème et oblige à passer aux nombres décimaux ou en arrondissant. Il aurait de nombreux avantages. Notamment 12 a plus de diviseurs que 10, donc plus simple pour les fractions. Aussi, décompte simple des mois, des heures, des degrés. Une année compte 12 mois. Un nombre en base 12 compte 12 chiffres: {1, 2, 3, 4, 5, 6, 7, 8, 9, A et B}. Exemple: Soit 6B4₁₂ => conversion en base 10: 6x12² + 11x12 + 4 = 864 + 132 + 4 = 1000. Douze a quatre diviseurs (outre 1 et 12) Demi, tiers, quart, sixième seraient des nombres entiers. Compter sur les doigts C'est le nombre de phalanges des quatre doigts opposés au pouce. Vestige Le compte des œufs à la douzaine et à la grosse (12 x 12). Et en typographie: 1 cicéro = 12 points. Charlemagne a introduit la livre (libra) vers l'an 800, divisée en vingt solidi (devenus sous, des sols ou des schillings), chacun de ceux-ci se divisant en douze denarii (devenus des deniers ou des pfennigs).
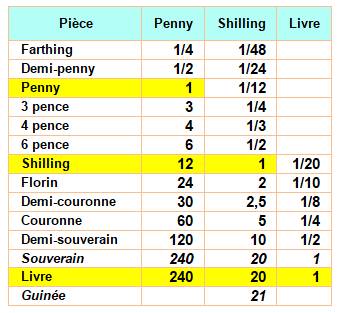
Système britannique avant décimalisation Les Britanniques utilisaient une pseudo-base 240 (Voir Vestige, ci-dessus) qui offrait l'avantage de pouvoir se partager en 2, 3, 4, 5, 6, 8, 10 et 12. La livre était divisée en 20 shillings (solidus), laquelle était divisée en 12 pence (denarius) et 20 x 12 = 240. Ils ont abandonné un tel système le 15 février 1971.
Le Florin Pseudo-base monétaire 144 née au milieu du XIIIe siècle.	Florin ou gulden = 12 sols ou gros Sol = 12 deniers
Mesure de longueur	1 pied = 12 pouces 1 pouce = 12 points

Voir Base 60

Commentaires

L'emploi de la douzaine remonte sans doute au fait que l'année compte approximativement douze lunaisons: la Terre fait le tour du soleil en un an et, pendant ce temps, la Lune exécute un peu plus de 12 rotations autour de la Terre.

Douze est un nombre comportant une grande quantité de diviseurs (1, 2, 3, 4, 6,12) ce qui permet de faire différentes sortes de parts de tarte; ce qui est moins facile avec 10 dont les diviseurs sont (1, 2, 5, 10). La division du cadran de l'horloge est un témoin de cette propriété. La journée compte conventionnellement 2 x 12 heures.

Le système de numération duodécimal est formé de 12 chiffres (0, 1, 2 …9, A, B). De sorte que notre 10 devient A et le 11 devient B. Le nombre suivant, notre 13 en décimal, est 10 en duodécimal. Le nombre 100 en duodécimal est équivalent à 144 en décimal (144 = 12x12)

Tolkien dans le Seigneur des Anneaux mentionne 12 douzaines comme une grosse dans la bouche des Hobbits.

Ah, si nous avions tous douze doigts!

Au lieu de compter en base décimale, comme il est naturel avec dix doigts, nous aurions utilisé la base duodécimale, beaucoup plus pratique.

En effet, 12 est un nombre abondant : la somme de ses diviseurs est supérieure à son double (1 + 2 + 3 + 4 + 6 + 12 = 28), alors que 10 est au contraire déficient (1 + 2 + 5 + 10 = 18).

Un nombre abondant permet davantage de divisions ayant pour résultat des nombres entiers… et donc un progrès des mathématiques plus rapide.

Au Moyen Âge, la base 12 était courante : douze pouces pour un pied, douze deniers pour un sou, etc.

Voir Nombre 6 / Hoha11, le gène responsable de la quantité de doigts / Myriapodes / Sept doigts

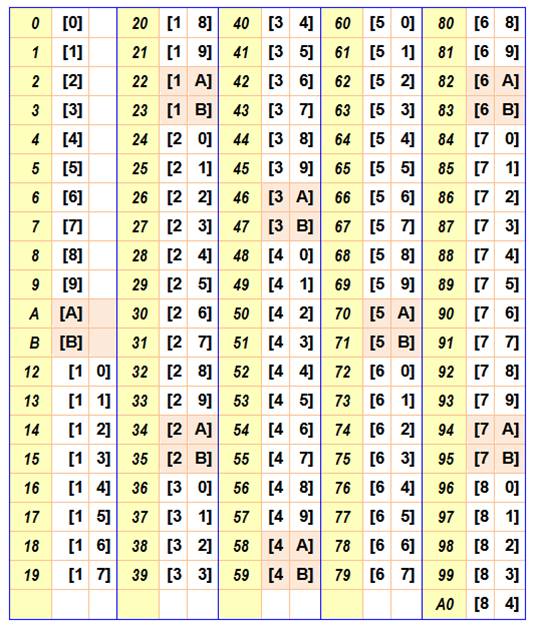
Table de conversion des nombres de 1 à 100 en duodécimal

A et B sont deux nouveaux chiffres: A représente 10 en décimal et B représente 11.

Exemple: 22 en décimal donne 1A en base 12, car 12 = 1 x 12 + 10

Voir Table avec autres bases / Autres tables – Index

ENGLISH CORNER

Dozen is another word for the number twelve. The dozen may be one of the earliest primitive groupings, perhaps because there are approximately a dozen cycles of the moon or months in a cycle of the sun or year.

The use of twelve as a base number is known as the duodecimal system (or dozenal).

Retour	Nombre 12 Expressions avec douze Demi-douzaine
Suite	Nom des petits et grands nombres Bases de numération
Voir	Calcul mental – Index Puzzles – Index
Cette page	http://villemin.gerard.free.fr/aNombre/Nb0a1000/N12.htm