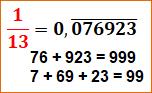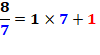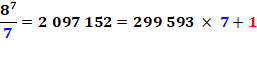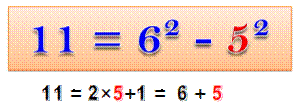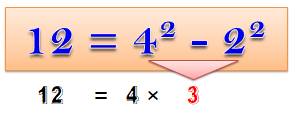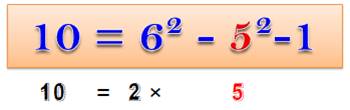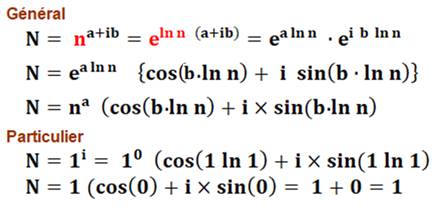NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 03/10/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 10		Page 20		Page 30		Page 40			Page 50
	Page 10 (180-199)		Page 11 (200-219)		Page 12 (220-239)		Page 13 (240-259)		Page 14 (260-279)
	Page 15 (280-299)		Page 16 (300-319)		Page 17 (320-339)		Page 18 (340-359)		Page 19 (360-379)

BRÈVES de MATHS – Page 13

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

240. Nombre 13
Propriétés Le nombre 13 est premier, jumeau avec 11. Il est permutable car 31 est aussi premier. C'est un nombre de Fibonacci: 1, 1, 2, 3, 5, 8, 13… Divisibilité par 13 Les nombres de la forme abcabc sont divisibles par 13: 123 123 / 13 = 9 471. C'est le cas notamment de 111 111 / 13 = 8 547. Curiosités 13 = 2² + 3² = 7² – 6² Mnémotechnique des nombres 13 a pour code mnémotechnique le mot TAMIS avec les consonnes sonores T pour 1 et M pour 3. D'autres mots avec T et M conviennent comme: tome, Tomas, timon, atome, étamer, intime …		Nombre dichotomique et trichotomique La période de l'inverse de 13 donne 999 lorsque coupée en deux et sommée; elle donne 99 lorsque coupée en trois et sommée. C'est une propriété fréquente pour les inverses des nombres premiers. Superstition Souvent rapporté aux douze Apôtres de la Cène, la croyance au 13 comme étant maléfique remonte à l'Antiquité. 12 est symbole d'harmonie; lui ajouter 1 détruit la perfection. Dans la Rome antique, les exécutions avaient lieu le 13. Le treizième tarot ne porte pas de nom; il représente la mort, la transition… Vendredi 13 Une année comporte au minimum un vendredi treize et au plus trois. Un mois qui commence un dimanche 1^er aura un vendredi 13.
Brèves associées	>>> Nombre 12 >>> Nombres de Fibonacci		>>> Nombre 14
Pour en savoir plus	>>> Nombre 13 – Culture >>> Nombre 13 – Maths >>> Nombre 13 – Superstition		>>> Nombres répétés >>> Nombres dichotomiques >>> Mnémotechnique

241. Grandeurs utilisées en électricité
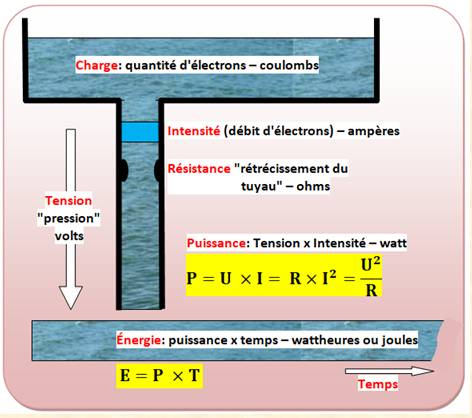
Six grandeurs CHARGE – coulombs (C) TENSION – volts (V) INTENSITÉ – ampère (A) RÉSISTANCE – ohms () PUISSANCE – watts (W) ÉNERGIE – joules (J) ou wattheure (Wh) Relations entre elles Voir les indications en jaune sur la figure. Sans oublier la loi d'Ohm: U = R x I
Analogie avec une chute d'eau Une chute d'eau très haute crée une grande force, une grande pression, une grande tension. Une grande intensité correspond à un grand débit; soit beaucoup d'eau (d'électrons) par seconde. Beaucoup d'eau avec grande force crée une grande puissance. Beaucoup de puissance pendant une longue durée engendre beaucoup d'énergie. Quant la résistance à l'écoulement de l'eau, ce peut être des aspérités dans le tuyau, des rétrécissements intempestifs … Tout ce qui empêche l'écoulement libre. S'il s'agissait d'une rivière, on parlerait des rochers dans le lit ou des méandres du cours d'eau, etc. En électricité, il s'agit des appareils qui consomment de l'énergie comme les moteurs et surtout de tous ceux qui chauffent (dissipation par effet Joule). Le réservoir d'eau symbolise la quantité d'eau disponible, soit, la quantité d'électrons; on dit la charge. Attention: l'analogie hydraulique a ses limites. Cette comparaison sert uniquement à aider à la mémorisation des grandeurs utilisées en électricité.
Pour en savoir plus	>>> Électricité – Approche >>> Loi d'Ohm		>>> Unités SI >>> Eau

242. Petit théorème de Fermat
Un théorème très utile en théorie des nombres. Il affirme qu'un nombre et sa puissance p, p étant un nombre premier, donnent le même reste lorsqu'on les divise par p. Exemple: le reste vaut 1 pour les deux divisions Avec ce théorème inutile de faire les calculs pour connaitre le reste d'une division. Exemples 12^13 divisé par 13, reste 12 (comme pour 12 /13) 13^13 divisé par 13, reste 0 (comme pour 13 /13) 14^13 divisé par 13, reste 1 (comme pour 14 /13)		Théorème On lit: quel que soit le nombre a appartenant à N (N est l'ensemble des nombres entiers) et quel que soit le nombre premier p, la différence entre la puissance p de a et a lui-même, est congru à 0 modulo p (ou donne un reste nul lorsque cette différence est divisée par p). Notez la concision de la formulation par rapport au texte explicite. Certes, il faut un peu d'habitude. Exemple particulier a = 2 Forme arithmétique Forme théorie des nombres
Brèves associées	>>> Petit théorème – Approche >>> Théorème de Fermat-Wiles		>>> Modulo
Pour en savoir plus	>>> Petit théorème de Fermat >>> Fermat (1607?-1665)		>>> Ensemble des nombres entiers

243. Calcul différentiel et intégral
Approche Prenons un phénomène modélisé par une courbe pas forcément très sympathique. Comment s'y prendre pour connaitre: son taux de variation: la pente de la courbe, sa dérivée; l'aire de la surface balayée: l'intégrale. Prenons un phénomène connu localement, comment imaginer le comportement d'ensemble ? En utilisant le calcul intégral. Exemple Si la fonction est la distance parcourue par un mobile, sa dérivée est la vitesse instantanée. Et, la dérivée de la vitesse est l'accélération. Si on connait la vitesse instantanée d'un mobile, pour reconstituer la distance parcourue on procédera à l'intégration de la vitesse. Découverte En 1684, Leibniz publie ses travaux sur le calcul différentiel et intégral, prenant de vitesse Newton et sa méthode des fluxions. Dans un premier temps la correspondance entre ces deux hommes attestent de leur respect mutuel. C'est l'entourage de Newton qui jalouse l'expansion de la méthode Leibniz en Europe et qui attise la polémique. C'est pourtant la méthode de Leibniz et ses notations, plus simple, qui va s'imposer.		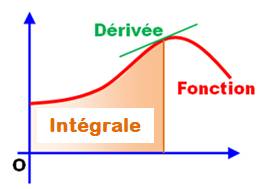Illustration Calcul différentiel: la pente de la courbe (sa tangente) tout le long de la courbe est appelée la fonction dérivée. On s'intéresse à la modulation de la courbe. Calcul intégral: la surface balayée par la courbe est appelée sa primitive. Son calcul est nommé: intégration. Double-face Dérivée et intégrale sont deux opérations inverses comme le sont la multiplication et la division.
Brèves associées	>>> Arithmétique	>>> Calcul et maths
Pour en savoir plus	>>> Calcul différentiel – Approche >>> Calcul intégral – Approche	>>> Dérivée – Liste >>> Primitives – Liste

244. Ontologie des maths
Qu'en pensez-vous? Est-ce que la propriété des nombres énoncée par le théorème de Fermat-Wiles existait avant que Fermant ne la formalise sous cette équation: N'existe pas pour n entier > 2 La réponse semble évidemment oui. Cette propriété était latente et n'attendait qu'à être révélée. L'humanité braque une torche mathématique sur le monde des nombres et, jour après jour, éclaire de nouvelles zones, révélant de nouvelles propriétés. Une propriété mathématique mise au jour est vraie pour toujours.			Kurt Gödel est connu pour avoir démontré qu'il impossible de poser des hypothèses minimales et en déduire une théorie mathématique complète. Il pourrait être sceptique et prétendre que les maths ne sont qu'inventions humaines. Pour lui, les concepts mathématiques "forment une réalité objective à part que nous ne pouvons pas créer ou modifier, mais simplement percevoir et définir". Platonisme mathématique ou réalisme mathématique: les entités mathématiques ont une existence objective. Elles ne sont pas une abstraction humaine. Le monde platonicien des mathématiques existe indépendamment de la réalité physique. Triangle de Penrose: monde physique, monde mental et monde platonicien des mathématiques.
Extrait du livre d'Edward Frenkel: Amours et Maths		Extrait consultable en e-book sur Internet
Brèves associées	>>> Théorème de Fermat-Wiles			>>> Infini
Pour en savoir plus	>>> Ontologie >>> Platon			>>> Kurt Gödel et l'incomplétude >>> Penrose

245. Amusements avec les carrés
Nombres impairs Tout nombre impair est la somme de deux nombres consécutifs dont la différence des carrés redonne le nombre initial. Motif amusant basé sur cette propriété 11 = 6 + 5 = 6² – 5² 111 = 56 + 55 = 56² – 55² 1111 = 556 + 555 = 556² – 555² … Justification algébrique (k+1)² – k² = k² + 2k + 1 – k² = 2k + 1 => ce nombre est impair. (k+1)² – k² – 1 = k² + 2k + 1 – k² – 1 = 2k => ce nombre est pair. (k+2)² – (k–2)² = k² + 2k + 4 – k² + 2k – 4 = 4k => ce nombre est divisible par 4.		Nombres divisible par 4 Tout nombre divisible par 4 est la différence des carrés de deux nombres situés de part et d'autre du quotient. Nombres pairs Tout nombre pair est la différence de carrés de deux nombres successifs moins 1, le plus petit étant la moitié du nombre initial. Normal: un nombre pair est égal à un nombre impair auquel on retire 1.
Brèves associées	>>> Identités remarquables		>>> Nombres pairs et impairs
Pour en savoir plus	>>> Nombres pairs / impairs et carrés

246. Un à la puissance i
Le nombre 1 multiplié k fois par lui-même reste égal à 1. Autrement-dit: 1^k = 1 Mais est-ce vrai pour 1 porté à la puissance imaginaire i ? La réponse tentante est "oui". Mais, comment le prouver. Pas si simple! Il faut d'abord examiner le cas d'un entier n porté à une puissance complexe (a + ib) et prendre sa forme exponentielle. Ensuite, on peut y introduire n = 1, a = 0 et b = 1 et obtenir le résultat cherché.		Dans la mesure ou ln (1) = 0, ce résultat est généralisable à toutes les puissances complexes de 1: 1^a + ib = 1.
Brèves associées	>>> Unités des puissances		>>> Nombres complexes
Pour en savoir plus	>>> Nombres portés à une puiisance complexe

247. Loi de l'étalement uniforme
Loi de Benford La loi de l'étalement uniforme de la partie fractionnaire est une loi simple qui est susceptible d'expliquer la loi de Benford ou loi du premier chiffre significatif: la probabilité de rencontrer un chiffre en tête d'un nombre va en décroissant du 1 (30%) au 9 (4,6%). Jean-Paul Delahaye		Étalement uniforme La loi énonce en gros que: parmi une collection de nombres réels pris au hasard, si on ne conserve que la partie fractionnaire, celle-ci sera uniformément répartie entre 0 et 1. Exemples [7.9, 3.7, 9.6, 8.3, 5.1, 7.4, 5.0, .40, .30, 9.7], [1, 0, 2, 2, 0, 1, 2, 0, 1, 1] sur 1000 valeurs [98, 98, 104, 94, 91, 96, 101, 114, 107, 97]
Brèves associées	>>> Théorie des nombres		>>> Ensembles des nombres
Pour en savoir plus	>>> Loi de Benford

248. Loi de Benford
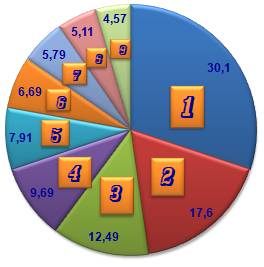
Loi de Benford ou loi du premier chiffre significatif La probabilité de rencontrer un chiffre en tête d'un nombre va en décroissant comme le montre le graphique. Historique En 1881, Simon Newcomb (1835-1909), un mathématicien et astronome, constate que les premières pages des tables de logarithmes sont plus usées que les autres. Il formule une loi qui tomba dans l'oubli. En 1938, Frank Benford, un physicien américain, redécouvre une loi du même type. Intérêt Cette loi est utilisée pour détecter les fraudes. Si les données son inventées, il est plus que probable qu'elles ne suivront pas la loi de Benford. 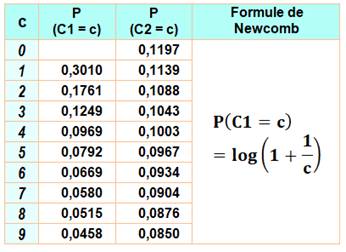La répartition sera probablement plus uniforme que pour des données réelles. Newcomb proposait The law of probability of the occurrence of numbers is such that all mantissae or their logarithms are equally like La loi de probabilité d'occurrence des nombres est telle que toutes les mantisses des logarithmes sont uniformes.		Probabilité d'occurrence du premier chiffre dans une série de nombres Table et formule de Newcomb C1 est le premier chiffre et C2, le deuxième
Pour en savoir plus	>>> Loi de Benford >>> Logarithmes	>>> Anglais: le bagage mimimum au bac

249. Mot de Fibonacci
Mot de Fibonacci Comme pour la suite de Fibonacci, on commence à poser deux valeurs de départ: M1 = 1 et = 0 On dit "mot" car les valeurs de départ peuvent être des lettres ou des symboles. Puis on fixe une règle de construction par récurrence: concaténation (juxtaposition) des deux derniers mots. M3 = M2M1 = 01 M4 = M3M2 = 010 M5 = M4M3 = 01001 M6 = M5M4 = 01001010 M7 = M6M5 = 0100101001001 La quantité de chiffres est égale au nombre de Fibonacci de même rang, celle de "0" au Fibonacci de rang inférieur et celle de "1" de rang un cran en dessous.		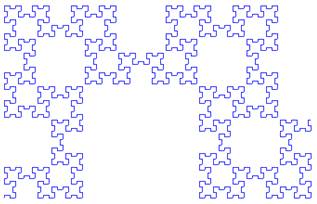Fractale du mot de Fibonacci En interprétant le mot binaire comme des instructions de progression, on obtient ce genre de jolie courbe. Propriétés Elle ne se recoupe jamais. Sa dimension fractale: 1, 637… Sa programmation avec le logiciel Scratch est très facile et de très bon effet (Voir le lien).
Brèves associées	>>> Suite de Fibonacci	>>> Suite de Fibonacci avec Scratch
Pour en savoir plus	>>> Mot de Fibonacci	>>> Fractale du mot de Fibonacci

250. Nombres S-Parfaits
Une idée de la construction Méthode de sélection des diviseurs telle que la somme de ces nouveaux élus soit égale au nombre initial; ce nombre est alors S-parfait. Historique C'est en 1996, qu'Andrew Granville propose ce type de nombres à Jean-Marie De Koninck et Aleksandar Ivié.		Valeurs 6, 24, 28, 96, 126, 224, 384, 496, 1 536 … Avec 6 et 28 qui sont de vrais nombres parfaits. Le nombre 126 est le seul S-parfait connu comportant trois facteurs distincts. Ils sont tous divisibles par 2, et souvent par une puissance de 2. Ex: 1 536 = 2^9 x 3.
Brèves associées	>>> Nombres parfaits >>> Nombres abondants, déficients et parfaits
Pour en savoir plus	>>> Nombres S-parfaits – Méthode d'élaboration

251. Multiplication mentale rapide
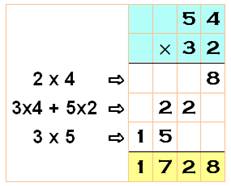
Prenons un exemple: 54 x 32. Se référer à l'illustration de gauche. Sur les colonnes de gauche comme de droite, on effectue simplement le produit des chiffres de la colonne. Quant au milieu, on effectue la somme des produits croisés. Se référer au tableau de droite. Ce tableau indique comment placer les produits obtenus, en les décalant. Le produit est la somme par colonne en tenant compte des retenues éventuelles.
Brèves associées	>>> Multiplication de nombres entiers >>> Multiplication rapide à pivot >>> Multiplication des grands nombres		>>> Multiplication par 111
Pour en savoir plus	>>> Multiplications mentales rapides		>>> Calcul mental – Index

252. Lemniscate
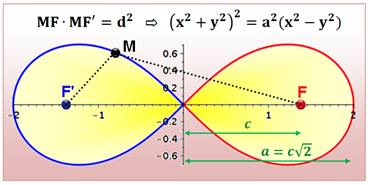
Courbe Courbe obtenue en déplaçant un point dont le produit des distances à deux points fixes (les foyers) est constant. Elle est en forme de huit, symbole de l'infini. Constante Comme Pi pour le cercle, la constante de la lemniscate permet le calcul de son périmètre P par rapport à sa dimension c. L = 5,2441… = P / c
Brèves associées	>>> Cercles et triangles équilatéraux		>>> Constantes mathématiques >>> Infini
Pour en savoir plus	>>> Lemniscate >>> Constante Pi= 3,1415…		>>> Forme 8 >>> Symbole de l'infini

253. Cryptologie
Cryptologie: science du secret, comprend: cryptographie: écriture secrète; cryptanalyse: analyse de l'écriture secrète. Cryptographie: protection des messages notamment durant leur transmission d'un émetteur vers un récepteur. Elle comprend: la cryptographie symétrique ou clé secrète, et la cryptographie asymétrique ou à clé publique.		Exemple le plus simple Le plus ancien système de codage de message consiste à substituer chaque lettre par la lettre située dans l'alphabet un peu plus loin. ABCD avec un décalage de 2 devient: CDEF. Faiblesse de la méthode Actuellement la méthode est archi-connue, mais au-delà de cela, ce type de méthode présente une faiblesse rédhibitoire. En français on connait la fréquence des lettres et alors, on sait reconnaître les plus fréquentes dans le message. Lettres les plus fréquentes en français: E A I S N R T O L U D
Pour en savoir plus	>>> Codage par décalage de lettres >>> Cryptologie – Introduction et Index		>>> Fréquence des lettres

254. Triangles dans le triangle
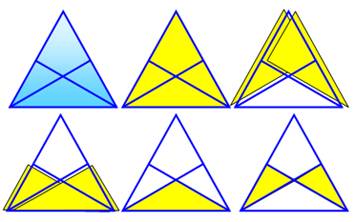
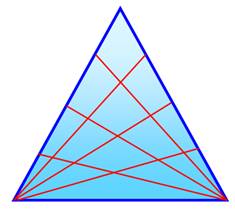
Combien de triangles dans le triangle bleu ? En jaune: 1 + 2 + 2 + 1 + 2 = 8 = 2^3 triangles		Et dans celui-ci ? On note n la quantité de segments découpés sur un des côtés Ce triangle bleu, avec n = 4, contient 4^3 triangles. Avec n quelconque, le triangle contient n^3triangles.
Brèves associées	>>> Somme de nombres consécutifs		>>> Droites dans le triangle
Pour en savoir plus	>>> Triangles dans le triangle		>>> Dénombrement – Index

255. Souris sur un triangle
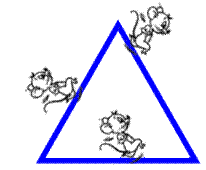
Énigme Trois souris se trouvent au sommet d'un triangle équilatéral. Soudain, chacune choisit son sens et s'élance sur le périmètre, toutes à la même vitesse. Quelle est la probabilité qu'elles ne rencontrent jamais ? Solution Chacune choisit un sens de parcours parmi 2. Soit 8 possibilités pour les trois souris (2x2x2 = 2^3). Elles ne se rencontrent jamais si elles tournent toutes dans le même sens. Soit 2 possibilités. La probabilité de non-rencontre est: 2/8 =1/4 = 25%.
Brèves associées	>>> Lapins et canards	>>> Pesée des quatre billes
Pour en savoir plus	>>> Probabilités – Calculs

256. Conversion binaire
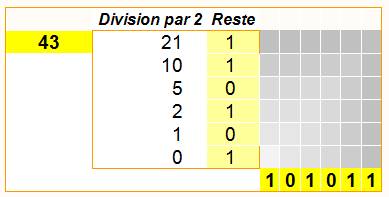
Décimale vers binaire 4310 = 1010112 Qui se lit: 43 en base 10 (base décimale) est égal à 101011 en base 2 (binaire) Explications La procédure consiste à diviser le nombre par 2 et à conserver le reste, puis faire la même chose avec le quotient. 43 = 2 x 21 + 1, je garde le 1 en poids fort (chiffre à gauche du nombre binaire) Je continue avec 21 = 2 x 10 + 1, etc.		Tableau de conversion décimal vers binaire
Binaire vers décimal 11012 = 1310 Qui se lit: 1101 en base 2 (binaire) est égal à 13 en base 10 (base décimale) Explications Le 1 à droite "pèse" 1; Le 0 qui suit contribue pour 0; Le 1 ensuite est dans la colonne de poids 2^2 = 4, il "pèse" 4; Le 1 final à gauche ajoute 2^3 = 8; et La somme des poids donne: 1 + 0 + 4 + 8 = 13		Tableau de conversion de binaire en décimal
Brèves associées	>>> Nombres 0 et 1 – Binaire		>>> Compter avec dix chiffres
Pour en savoir plus	>>> Numération binaire		>>> Bases de numération

257. Rencontres sportives
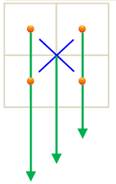
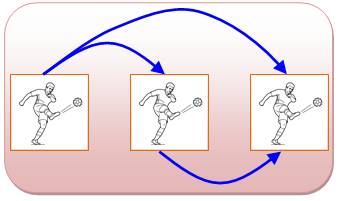
Énigme Ce club comporte 10 équipes et le tournoi consiste à ce que chaque équipe rencontre chacune des autres et cela deux fois pour le match retour. Combien de matchs? Trois équipe – Un match (illustration) La première équipe joue avec la 2 puis le 3, soit deux matchs; La deuxième équipe joue avec la 3, soit un match. Bilan pour trois équipes: 2 + 1 = 3 matchs Dix équipe – Deux matchs La première équipe joue contre les 9 autres, etc. Bilan: 2 fois (9 + 8 + … + 1) = 2 x (9 x 10) / 2 = 90 matchs.		Rencontre entre trois équipes: 3 matchs
Brèves associées	>>> Somme: 1 + 2 + 3 + 4 + …		>>> Factorielle
Pour en savoir plus	>>> Types de dénombrements		>>> Dénombrement – Index

258. Hexagone et dodécagone
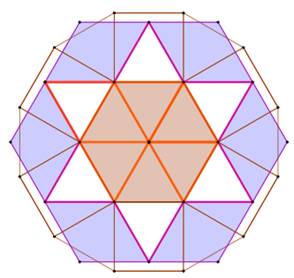
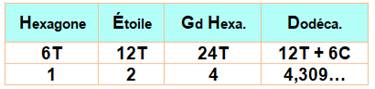
Construction Un hexagone central, autour duquel on construit une étoile à six branches, un grand hexagone (limité en bleu) et un dodécagone. Aire de ces polygones Hexagone central: 6T (six fois le triangle équilatéral). Étoile: 6T + 6T = 12T Grand hexagone: 12T + 12T = 24T Dodécagone: 6T + 6T + 6C = 12T + 6C Rapports entre toutes ces surfaces		Hexagone et dodécagone
Brèves associées	>>> Rosace – Hexagone	>>> Angles dans trois carrés
Pour en savoir plus	>>> Hexagone	>>> Hexagone sous toutes les coutures

259. Nombres de Harshad
Définition Nombre divisible par la somme de ses chiffres. Exemple de 10 à 50 10, 12, 18, 20, 21, 24, 27, 30, 36, 40, 42, 45, 48, 50 Chaine de Harshad (nombres consécutifs)		Le nombre 18 est divisible par (1 + 8 = 9)
Brèves associées	>>> Nombres géométriques	>>> Pépites numériques
Pour en savoir plus	>>> Nombres de Harshad >>> Nombres par leur nom – Portail	>>> DicoNombre – Portail

Retour	Brèves de maths – Page 12
Suite	Brèves de maths – Page 14
Voir	Voir liens en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve13.htm