|
|||||||||||||||||||||||||||||||||||
![]()
|
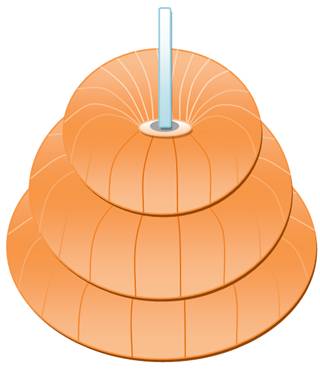
Tour de Hanoi ou de Brahmâ ou tours de Hanoi Casse-tête classique dont
la résolution suit en fait le principe du codage Gros-Gray:
changer un seul élément à la fois. Même principe de résolution que le baguenaudier. Tour de Brahmâ: objet d'un culte religieux Hindouiste. Intérêt: excellent exemple de procédure récursive, régal des programmeurs. |
|
|
|
|
Il
s'agit de la tour de Brahmâ de 64 disques simplifiée à 8 disques. Il
faut 28 – 1 = 255 coups pour le terminer. Lucas en
fait un petit livre au titre plein de mystère en 1882: La tour de
Hanoï Véritable
casse-tête annamite Jeu
rapporté du Tonkin par le professeur N. Claus (de Siam) du collège Mandarin
Li-Sou-Stian Claus est
une anagramme de Lucas et Li-Sou-Tina
de Saint Louis. Il
commence son ouvrage par: D'après une
vieille légende indienne, les brahmes se succèdent depuis bien longtemps sur
les marches de l'autel dans le temple de Bénarès pour exécuter le déplacement
de la Tour Sacré de BRAHMA aux
soixante-quatre étages en or fin, garnis de diamants de Golconde. Quand tout
sera fini, la tour et les brahmes tomberont, et ce sera la fin du monde! Le jeu
original de Lucas est conservé au Conservatoire des Arts et métiers à Paris.
|
|
|
|
||
|
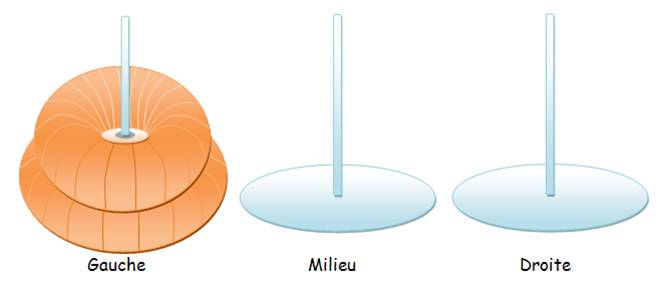
Règle générale
|
||
|
Position de départ
21 0 0 Étape 1
2 1 0 Étape 2
0
1 2 Étape 3
0
0 21 |
|
|
|
|
||||
|
|
321 32 3 3 0 1 1 0 |
0 0 2 21 21 2 0 0 |
0 1 1 0 3 3 32 321 |
|
|
|
|||||
|
|
|||||
|
Déplacement du 1
(petit anneau) |
4321 432 43 43 4 41 |
0 1 1 0 3 3 |
0 0 2 21 21 2 |
|
|
|
Déplacement des
autres chiffres (autres anneaux) |
41 41 4 0 0 2 21 21 2 0 0 |
3 32 321 321 32 3 3 0 1 1 0 |
2 0 0 4 41 41 4 43 43 432 4321 |
|
|
|
|
|
|
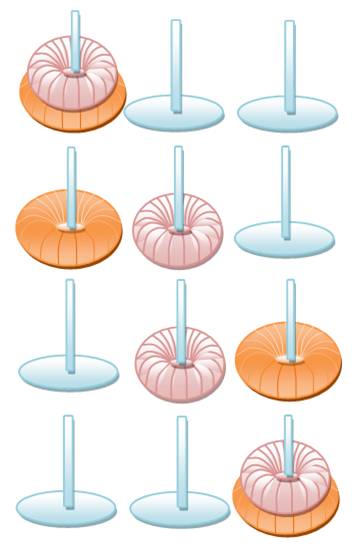
La règle est simple:
La résolution exige 2n – 1
mouvements, si n est la quantité d'anneaux. Voir Échiquier
et les grains de blé Note Récemment, des
mathématiciens ont prouvé que, quel que soit le nombre de disques, les
déplacements ne se répètent jamais consécutivement dans le même ordre: jamais
2 fois de suite AB ou AB, AC, etc. Commentaires
|
|
|
|
||||
|
|
54321 5432 543 543 54 541 541 54 5 5 52 521 521 52 5 5 |
0 1 1 0 3 3 32 321 321 32 3 3 0 1 1 0 |
0 0 2 21 21 2 0 0 4 41 41 4 43 43 432 4321 |
|
|
|
0 1 1 0 3 3 32 321 321 32 3 3 0 1 1 0 |
5 5 52 521 521 52 5 5 54 541 541 54 543 543 5432 54321 |
4321 432 43 43 4 41 41 4 0 0 2 21 21 2 0 0 |
|
|
|
|
|
5,8 1011 Nombre d'années
pour terminer la tour de Brahmâ. Calcul Pour les 64 disques de
la tour de Brahmâ, on montre que le nombre minimum de
mouvements est égal à 264 – 1. C'est le même nombre que pour les grains de blé de l'échiquier, soit
1,84 1019 . À raison
d'un mouvement par seconde, soit 31 558 000 mouvements par an, il faudra 584
milliards d'années (5,8 1011). Soit 42,6 fois plus que l'âge de l'Univers
estimé à 13,7 milliards d'années. Or, selon cette légende indienne, l'Univers a, à peine, vécu et il lui reste encore quelques années
à vivre! (5,8 1011 / 1,5 1010 = 38 fois l'âge de
l'Univers). Légende Dans le grand temple de Bénarès, sous le dôme qui marque le centre du
monde, repose un socle de cuivre équipé de trois aiguilles verticales en
diamant de 50 cm de haut. À la création, Dieu enfila 64 plateaux en or pur sur une des aiguilles,
le plus grand en bas et les autres de plus en plus petits. C'est la tour de
Brahmâ. Les moines doivent continûment déplacer les disques de manière que
ceux-ci se retrouvent dans la même configuration sur une autre aiguille. La règle de Brahmâ est simple: un seul disque à la fois et jamais un
grand plateau sur un plus petit. Arrivé à ce résultat, le monde tombera en poussière et disparaîtra. |
|
Voir Âge
de l'Univers
|
|
|
|
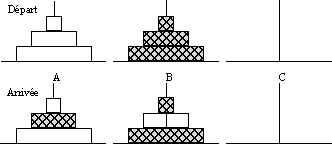
Solution
AC - BC - AB - CB -
CB - AC - BA - BA - BC - BC - AC - AC - BA - CA -
CA - CB - CB - AC - AC - BA - BA - CA - CA - CB -
AC - AC - AB - CB - CA. |
|
|
|
|
|
|
|
Voir DicoCulture
|
|
|||
|
Si M est la quantité de
mouvements à effectuer
|
Si on sait faire cette opération, on sait
les faire toutes. |
||
|
On démontre par récurrence forte que: |
Mn |
= 2n – 1 |
|
|
Point de départ. |
M1 |
= 2 – 1 = 1 C'est vrai |
|
|
Hypothèse de récurrence:
relation vraie pour tous les entiers i jusqu'à k. |
Mi |
= 2i – 1 |
|
|
Ce qu'il faut démonter. |
Mk |
= 2k – 1 |
|
|
Nous connaissons la formule
de récurrence. |
Mk |
= 2 x Mk-1 + 1 |
|
|
Avec notre hypothèse. |
|
= 2 x (2k – 1 – 1)
+ 1 |
|
|
Calculs. |
|
= 2k – 2 + 1 |
|
|
Finalement. |
|
= 2k – 1 |
|
|
|
||
|
|
En
2014, Thierry Bousch, université d'Orsay, démontre que la formule de Dudeney
est bien la formule minimale. Spécialiste
des systèmes dynamiques, sa méthode est originale. Il construit des chemins
dans le graphe des possibilités. Il analyse des systèmes perturbés: sur la
tige initiale, il manque des disques sans que l'on sache lesquels… |
|
|
La formule de Dudeney donnant la quantité de mouvements pour N disques
sur quatre tiges: |
avec delta n, la racine triangulaire par défaut de n,
c'est-à-dire le plus grand entier p tel que:
|
|
Anglais: four-peg variant of the Towers of Hanoi
|
|
||
|
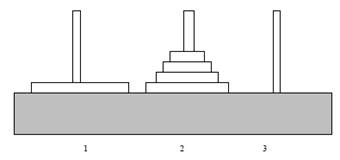
Présentation Similaire à la tour de Hanoï
à quatre tiges, mais la quatrième est centrale, et elle sert de pivot aux
mouvements: une pièce ne peut être déplacée que vers la tige centrale ou de
la tige centrale vers une des trois tiges périphériques. |
Le jeu
Source
image: La tour de Stockmeyer
– Maths-en-Jeans |
|
|
Quantité de mouvements La solution minimale avec quatre disques exige vingt mouvements. Avec cinq disques, il en faut au minimum trente-deux. Historique C'est en 1994 que Paul Stockmeyer propose cette variante de la tour de
Hanoï. Il a conjecturé, comme E. Dudeney, que la quantité minimale de
mouvements est le double de la somme des nombre 3-friables. La preuve en a
été apportée en 2017 par Thierry Boush. |
Nombres 3-friables La quantité de mouvements pour k disques est égale au double de la
somme des k plus petits nombres
3-friables. Ces nombres sont de la forme 2a٠3b. Ces sont 1, 2, 3, 4, 6, 8, 9, 12 … dont la double-somme pour k = 4 est
20, et celle pour k = 5 est 32. |
|
Anglais: In 1994, Paul Stockmeyer proposed a four-peg variant
of the Tower of Hanoi puzzle
Voir Brève 56-1101
Solution de la tour de Stockmeyer
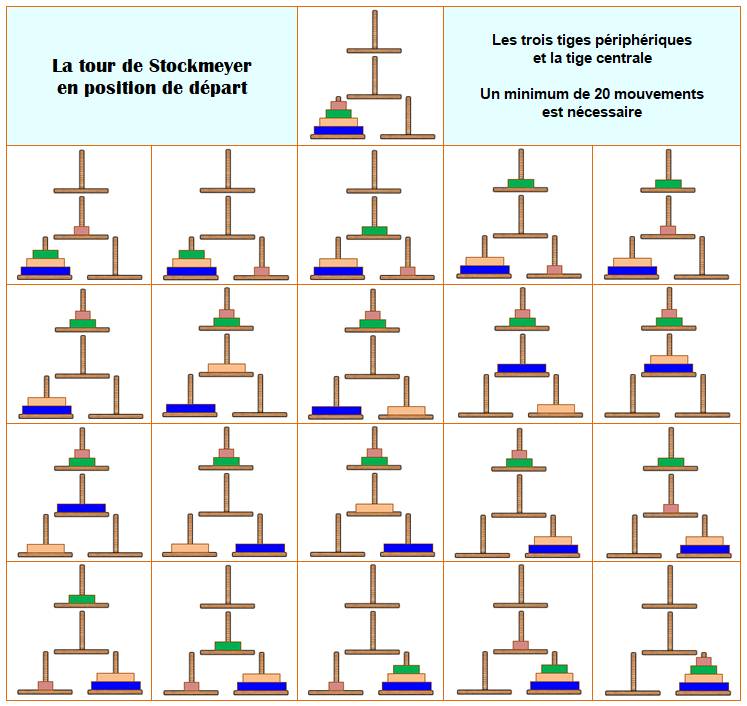
Illustration présente en
Les entiers friables – Jean-Paul Delahaye – Pour la Science N539 septembre 2022
![]()
|
Voir |
||
|
Livre |
|
|
|
Sites |
|
|
|
Cette page |
||
![]()