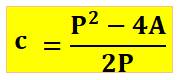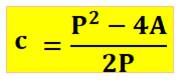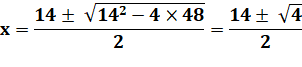Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 10/12/2023 M'écrire Brèves de Maths

INDEX Triangle rectangle Triangle Géométrie	Triangles rectangles
	Triangles	Rectangle	Isiaque	Propriétés diverses
		Congruents	de Pythagore	Constructions
	Résolution Aire et Périmètre		Toutes les autres résolutions

Triangle RECTANGLE Résolution avec Aire et Périmètre On connait A, l'aire du triangle rectangle et P, son périmètre, alors l'hypoténuse c est calculé avec cette expression => Nous allons également calculer la longueur des deux autres côtés.
	Sommaire de cette page >>> Triangle rectangle entier >>> Résolution avec Aire et Périmètre	Débutants Triangle Glossaire Triangle

Triangle rectangle entier		haut
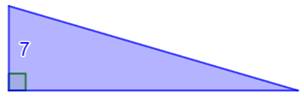
Problème Pour commencer simplement: trouver le périmètre et l'aire de ce triangle rectangle entier dont l'un des côtés vaut 7 cm. Solution	Figure initiale Solution Note: un triangle entier est un triangle dont toutes les longueurs sont représentées par des nombres entiers.

Résolution avec Aire et Périmètre		haut
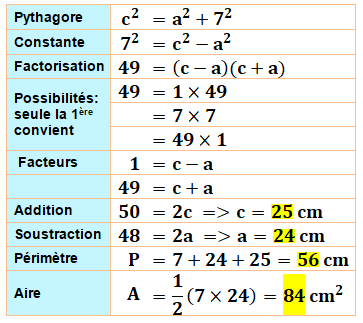
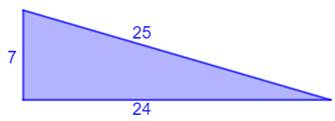
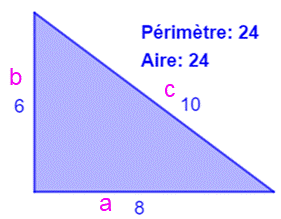
Construction Un triangle rectangle. Son aire est 24 et son périmètre est aussi 24. Retrouver la longueur de chacun des trois côtés. Piste Nous disposons de deux équations (A et P) auxquelles on ajoute le théorème de Pythagore. Soit trois équations pour trois inconnues. Calculs	Triangle rectangle avec ses mesures Un calcul littéral donnerait Voir Le calcul Somme et Produit Comment calculer deux nombres dont on connait la somme et le produit ? Ils sont racines de cette équation du second degré: x² – Sx + P = 0
Identité remarquable Comment transformer la somme des carrés (a² + b²) en une somme au carré (a + b)² ? En ajoutant 2ab de chaque côté. Car: (a+ b)² = a² + b² + 2ab Nous obtenons une identité remarquable.	Résolution de l'équation du second degré x² – 14x + 48 = 0

Voir Brève 56-1105

Haut de page

Retour	Calculs – Aire et Périmètre Résolution des triangles Triangle équilatéral Triangle rectangle – Constructions
Suite	Triangles rectangles entiers – de Pythagore Triangles rectangles particuliers Triangle rectangle – Index
Voir	Losange Puzzle chinois Rectangle Triangle – Index Types de triangles
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Types/TriaRecP.htm