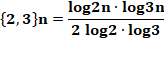|
Édition du: 15/04/2025 |
|
INDEX Facteurs et exposants
spéciaux |
Types de Nombres – Diviseurs |
|||
|
Semi-parfaits (SP) |
||||
![]()
|
Nombres FRIABLES ou
lisses* Les nombres dont les facteurs sont
inférieurs à k+1 sont des nombres k-friables. Exemple: 30 = 2 x 3
x 5 est un 5-friable. Notion utile en théorie des nombres, notamment en cryptographie. Inventée par Leonard
Adleman, co-inventeur du code RSA. Les 5-friables sont
aussi appelés nombres réguliers ou nombres de Hamming. Voir genèse en nombres
sans grands facteurs. |
||
|
|
Sommaire de cette page >>> Nombres friables >>> Liste >>> Diagramme de Hasse des
nombres réguliers >>> Programmation |
Débutants Glossaire |
Anglais: Friable numbers or smooth numbers
|
Entier
strictement positif tel que tous ses facteurs premiers sont inférieurs ou
égaux à une borne k donnée. |
10 800 = 24 x 33 x 52
est un 5-friable Il est aussi 7-friable, etc. |
|
|
Un
ultrafriable ou ultralisse est tel que
ses diviseurs en pn sont inférieurs ou égaux à une borne k donnée. |
10 800 = 24 x 33 x 52
est un
25-ultrafriable |
|
Voir Brève 56-1100 / Brève 20-396
|
2-friables Ce sont les puissances de 2 |
1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024,
2048, 4096, 8192, 16384, 32768, 65536, 131072, 262144, 524288, 1048576,
2097152, 4194304, 8388608, 16777216, 33554432, 67108864, 134217728, 268435456,
536870912, 1073741824, 2147483648, 4294967296, 8589934592 … Ils sont 7 jusqu'à 100, 10 jusqu'à 1000 et 14
jusqu'à 10 000. |
|
|
3-friables Nombres en 2p.3q Notation: {2,3}n |
1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 27, 32, 36, 48,
54, 64, 72, 81, 96, 108, 128, 144, 162, 192, 216, 243, 256, 288, 324, 384,
432, 486, 512, 576, 648, 729, 768, 864, 972, 1024, 1152, 1296, 1458, 1536,
1728, 1944, 2048, 2187, 2304, 2592, 2916, 3072, 3456, 3888, 4096, 4374, 4608
… Ils sont 20 jusqu'à 100 et 40 jusqu'à 1000 et 67
jusqu'à 10 000. Seuls 1, 2, 3 et 6 sont 3-ultrafriables. La somme des inverses de ces nombres vaut 3. Il
est égal au produit des deux suites géométriques: inverse des carrés et
inverses des cubes. Ce produit restitue tous les nombres 3-friables. À partir de 9, les 3-friables ne sont jamais
consécutifs – Démontré par Gersonide
(1288-1344). Ramanujan
donne cette formule pour calculer les nombres3-friables, formule
approximative mais d'une très grande précision:
Ces nombres se retrouvent dans la solution de la tour de Stockmeyer: la
solution du jeu à k disques est égale à la double-somme de k plus petits
nombre 3-fiables. |
|
ou Nombres réguliers ou Nombres de Hamming Nombres en 2p.3q.5r Notez que p, q et
r peuvent prendre la valeur 0. Les nombres réguliers divisent les
puissances de 60 (comme celles de 30) |
1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 16, 18, 20,
24, 25, 27, 30, 32, 36, 40, 45, 48, 50, 54, 60, 64, 72, 75, 80, 81, 90, 96,
100, 108, 120, 125, 128, 135, 144, 150, 160, 162, 180, 192, 200, 216, 225,
240, 243, 250, 256, 270, 288, 300, 320, 324, 360, 375, 384, 400, 405, 432,
450, 480, 486, 500, 512, 540, 576, 600, 625, 640, 648, 675, 720, 729, 750,
768, 800, 810, 864, 900, 960, 972, 1000, 1024, 1080, 1125, 1152, 1200, 1215,
1250, 1280, 1296, 1350, 1440, 1458, 1500, 1536, 1600, 1620, 1728, 1800, 1875,
1920, 1944, 2000, … Ils sont 34 jusqu'à 100 et 86 jusqu'à 1000 et 175
jusqu'à 10 000. Les 66 non-5-friables
jusqu'à 100: Ce sont les nombres premiers supérieurs à 5 et
leurs multiples 7, 11, 13, 14, 17, 19, 21, 22, 23, 26, 28, 29,
31, 33, 34, 35, 37, 38, 39, 41, 42, 43, 44, 46, 47, 49, 51, 52, 53, 55, 56,
57, 58, 59, 61, 62, 63, 65, 66, 67, 68, 69, 70, 71, 73, 74, 76, 77, 78, 79,
82, 83, 84, 85, 86, 87, 88, 89, 91, 92, 93, 94, 95, 97, 98, 99. Les 12 nombres 5-ultrafriables
: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60. |
Diagramme de Hasse des nombres réguliers jusqu'à 50: tous les multiples
de 2, 3 et 5
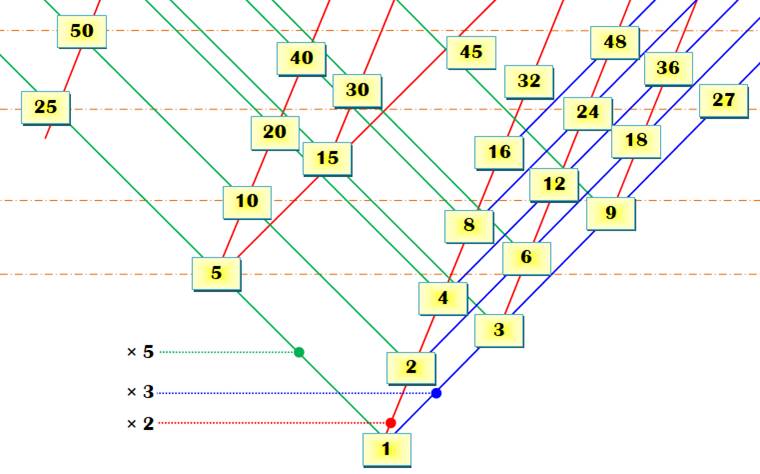
On
retrouve cette figure dans l'article de J.-P. Delahaye cité en référence
|
7-friables Nombres en 2p.3q.5r.7s |
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 15, 16,
18, 20, 21, 24, 25, 27, 28, 30, 32, 35, 36, 40, 42, 45, 48, 49, 50, 54, 56,
60, 63, 64, 70, 72, 75, 80, 81, 84, 90, 96, 98, 100, 105, 108, 112, 120, 125,
126, 128, 135, 140, 144, 147, 150, 160, 162, 168, 175, 180, 189, 192, 196,
200, 210, 216, 224, 225, 240, 243, 245, 250, 252, 256, 270, 280, 288, 294,
300, 315, 320, 324, 336, 343, 350, 360, 375, 378, 384, 392, 400, 405, 420,
432, 441, 448, 450, 480, 486, 490, 500, 504, 512, 525, 540, 560, 567, 576,
588, 600, 625, 630, 640, 648, 672, 675, 686, 700, 720, 729, 735, 750, 756,
768, 784, 800, 810, 840, 864, 875, 882, 896, 900, 945, 960, 972, 980, 1000,
1008, … Ils sont 46 jusqu'à 100 et 141 jusqu'à 1000 et
338 jusqu'à 10 000. Les 54 nombres non-7-friables
jusqu'à 100 11, 13, 17, 19, 22, 23, 26, 29, 31, 33, 34, 37, 38,
39, 41, 43, 44, 46, 47, 51, 52, 53, 55, 57, 58, 59, 61, 62, 65, 66, 67, 68,
69, 71, 73, 74, 76, 77, 78, 79, 82, 83, 85, 86, 87, 88, 89, 91, 92, 93, 94,
95, 97, 99. Les 24 nombres 7-ultrafriables
: 1, 2, 3, 4, 5, 6, 7, 10, 12, 14, 15, 20, 21, 28, 30, 35, 42, 60, 70, 84,
105, 140, 210, 420. |
|
11-friables Notez que un nombre
p-friable, avec p un nombre premier, le reste jusqu'au nombre q – 1, q étant
le premier suivant Le plus petit nombre non k-friables est le nombre
premier suivant. Pour 11, c'est 13. |
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 14, 15,
16, 18, 20, 21, 22, 24, 25, 27, 28, 30, 32, 33, 35, 36, 40, 42, 44, 45, 48,
49, 50, 54, 55, 56, 60, 63, 64, 66, 70, 72, 75, 77, 80, 81, 84, 88, 90, 96,
98, 99, 100 … Ils sont 55 jusqu'à 100 et 192 jusqu'à 1000 et
522 jusqu'à 10 000. Les 45 nombres non-7-friables
jusqu'à 100 13, 17, 19, 23, 26, 29, 31, 34, 37, 38, 39, 41,
43, 46, 47, 51, 52, 53, 57, 58, 59, 61, 62, 65, 67, 68, 69, 71, 73, 74, 76, 78,
79, 82, 83, 85, 86, 87, 89, 91, 92, 93, 94, 95, 97. Les 96
nombres 11-ultrafriables: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 14, 15,
18, 20, 21, 22, 24, 28, 30, 33, 35, 36, 40, 42, 44, 45, 55, 56, 60, 63, 66,
70, 72, 77, 84, 88, 90, 99, 105, 110, 120, 126, 132, 140, 154, 165, 168, 180,
198, 210, 220, 231, 252, 264, 280, 308, 315, 330, 360, 385, 396, 420, 440,
462, 495, 504, 616, 630, 660, 693, 770, 792, 840, 924, 990, 1155, 1260, 1320,
1386, 1540, 1848, 1980, 2310, 2520, 2772, 3080, 3465, 3960, 4620, 5544, 6930,
9240, 13860, 27720. |
|
|
Commentaires Réinitialisation et appel aux logiciels de
théorie des nombres. Déclaration d'un liste L qui contiendra les
nombres k-friables. Ici k = 7. Boucle d'analyse des entiers n. Recherche des facteurs premiers en F, leur
quantité en q et un indicateur T mis à un, supposant que le nombre analysé
est un fiable. Analyse des facteurs et mise à 0 de T si un facteur dépasse k. Si l'indicateur T est resté à un, le nombre est
déclaré friable et placé dans la liste L. En fin de programme, impression de L. En bleu, le résultat du traitement. |
|
Voir Programmation – Index
* FRIABLES ou LISSES
|
Trouver un vocable pour "nombres sans grand facteur"
… Les nombres ronds de
Hardy ont fait long feu. Ronald Lin
Rivest proposa le qualificatif
"smooth" ou "lisse" en français. Une quête collective pour un meilleur choix fut
entreprise notamment avec Tenenbaum qui aboutit au mot "friable".
Bien approprié car suggère qui est facile à factoriser. De plus, le terme est
le même en anglais. Et, c'est ce qualificatif qui tend à se répandre
dans la littérature mathématique de tout pays. |
Selon G. Tenebaum (voir livre en référence)
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
|
|
|
Livre Article |
|
|
Cette
page |