|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
BRÈVES de MATHS – Page 12 Un millier de faits et chiffres sur les nombres et les
mathématiques
En principe ces pages sont très abordables sans
connaissances particulières de maths. Elles sont proposées dans un ordre
quelconque favorisant la découverte de sujets multiples. |
Anglais: Facts and figures about numbers and mathematics
220. Boules de couleurs |
|
|||
|
Nous disposons de 2 boules de 2 couleurs. Combien de possibilités,
sachant que les boules peuvent être de la même couleur? Elles sont toutes les deux de la même couleur ou alors de couleurs 3 boules de 2 couleurs Dans ce cas, la première boules peut être verte ou rouge, avec à
chaque fois toutes les possibilités avec deux couleurs. Soit 2 x 4 = 8
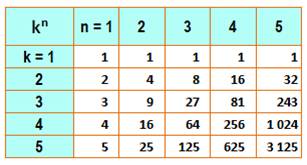
possibilités 5 boules de 3 couleurs La table de droite, pour n = 5 et
k =3, indique que la quantité de possibilité de colorer 5 boules de 3
couleurs est 35 = 243 |
Dénombrement Chaque boule est susceptible de prendre l'une des deux couleurs: 2
fois pour la première; 2 fois pour la deuxième et 2 fois pour la troisième.
Au total: 2 x 2 x 2 = 23 = 8 possibilités. Cas
général Aves k couleurs, il y a k possibilités pour chaque boule. Avec n boules,
il y a kn possibilités. Table des possibilités
|
|||
|
Pour en savoir plus |
>>>
Boules et couleurs |
>>>
Dénombrement – Débutants >>>
Dénombrement – Index |
||
221. Nombre 12 – Douze |
|
|||
|
Identité: 12 = 2² x 3
Diviseurs: 1, 2, 3, 4, 6, 12; Somme: 28 C'est un nombre abondant car 28 – 12 = 14 > 12. C'est le plus petit. 12, c'est une douzaine; 12 x 12 = 12² = 144, c'est une grosse. Propriétés Le nombre 12 est pair. Sa quantité de diviseurs explique son adoption
pour compter et partager (shilling = 12 pences) comme pour les heures ou pour
le commerce (œufs). Curiosités 12 = 3 + 4 + 5
et 6 + 7 + 8 = 21 (son retourné). 12 = 1! x 2! x
3! 400 / 33 =
12,121212… 12² = 144
et 441 = 21² Biologie Les personnes atteintes d'hexadactylie sont plus
nombreuses que ce que l'on croit: ils ont 2x6 doigts aux mains. Poésie:
alexandrin = vers à douze pied. Ex: On a
souvent besoin d'un plus petit que soi. |
Un polygone à 12 côtés est un dodécagone. Un polyèdre à 12 faces est un dodécaèdre. Un cube comporte 12 arêtes. Pentaminos Il existe 12 manières différentes d'assembler cinq
carrés et former les pentaminos.
La journée compte deux fois 12 heures, soit deux tours d'horloge pour la
petite aiguille. Un jour = 1 440 minutes = 10 x 12². |
|||
|
Brèves associées |
>>> Nombre 11 |
>>>
Nombre 13 |
||
|
Pour en savoir plus |
>>>
Nombre 12 – Culture >>>
Nombre 12 – Maths >>>
Horloge |
>>>
Base 12 >>>
Nombres abondants >>>
Dodécagone >>>
Pentaminos |
||
222. Le duo Babbage / Ada |
|
|||
|
Charles Babbage (1791-1871) |
Ada Lovelace (1815-1852) |
|||
|
Premier ordinateur du monde
Machine analytique de Babbage Caractéristiques Elle
fonctionne en base 10 (pignons dentés à 10 positions); précision à 40
décimales; une mémoire (magasin) de 1000 nombres de 50 chiffres. Elle est pilotée
(programmée) à l'aide de cartes perforées. Son
fils fera la démonstration de son véritable fonctionnement. Elle sera
effectivement construite en 1991 et fonctionnera comme prévu. |
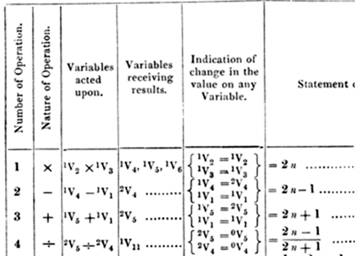
Premier programme informatique au
monde
Ce programme est destiné à fonctionner sur une
machine. C'est un algorithme de calcul des nombres de Bernoulli, développé
par Ada. Femme mathématicienne et
informaticienne Malgré sa santé fragile, elle étudie et développe
les mathématiques avec Mary Somerville et Auguste De Morgan. Elle est passionnée par les travaux de Babbage
qu'elle rencontre à 17 ans. En 1943, à 27 ans, elle publie un mémoire
exceptionnel montrant tous les usages de telles machines, au-delà du simple
calcul numérique. |
|||
|
Pour en savoir plus |
>>>
Charles Babbage >>>
Ada Lovelace |
>>>
Ordinateur – Fonctionnement >>>
Nombres de Bernoulli |
||
223. Triangles magiques |
|
|||
|
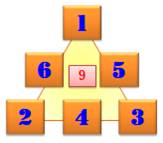
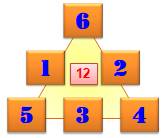
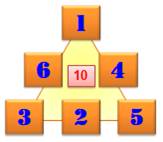
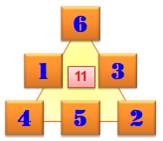
Consignes Comment disposer les nombres de 1 à 6 de sorte
que la somme sur chaque côté du triangle soit identique. Solutions Il existe seulement quatre solutions de base et toutes les rotations et réflexions
possibles. Remarquez que les triangles de droites sont les
compléments à 7 de ceux de gauche: 1 + 6 = 7, 5 + 2 = 7, 3 + 4 = 7 Sommes magiques En ajoutant les trois sommes: 3S = tous les
nombres de 1 à 6 (= 21) plus les sommets (qui comptent double). Au minimum, les sommets valent 1, 2 et 3 et la
somme devient: 21 + 1 + 2 + 3 = 27 pour 3S. Soit: Smin = 27 / 3 = 9 Au maximum, les sommets valent 3, 4 et 5 et la
somme devient: 21 + 4 + 5 + 6 = 36 pour 3S. Soit: Smax = 36 / 3 = 12. |
Les quatre seules solutions
Trouver les solutions Le calcul montre que seules ces quatre sommes
magiques 9, 10, 11 et 12 sont possibles. Avec ces sommes magiques et si peu de nombres à placer, il est facile
de trouver les arrangements qui conviennent. Ce sont les partitions de la somme magique, comme
9, avec trois nombres différents parmi 1, 2, 3, 4, 5 et 6. Il n'y a que trois
possibilités: |
|||
|
Brèves associées |
>>> Carrés
magiques 3x3 >>> Carrés
magiques 5x5 |
>>> Carrés
alpha-magiques |
||
|
Pour en savoir plus |
>>>
Polygones à périmètre magique |
>>>
Triangles >>>
Partition des nombres |
||
224. Cercles et triangles équilatéraux |
|
|||
|
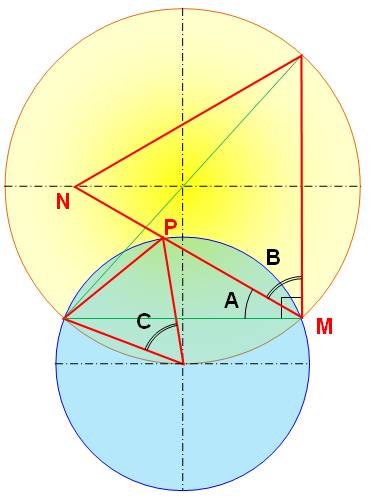
La figure Deux
cercles et deux triangles équilatéraux construits sur les cordes de la
manière indiquée. Propriété
remarquable quelle que soit la position du point M: P est
toujours sur MN. Démonstration On suppose MN et MP non alignés et on calcule les
angles. Angles B et C = 60° dans les triangles
équilatéraux. Angle A + B = 90° avec le triangle inscrit ayant
un diamètre pour hypoténuse. Angle A, avec MN pour côté: 90 – 60 = 30° Angle A', avec MP pour côté: 1/2 de C = 30°, car
ils interceptent le même arc. Les angles A et A' sont égaux. Conclusion, MP et MN ont
la même orientation, les points M, P et N sont alignés. Le sommet P du petit
triangle est situé sur un des côtés du grand triangle. |
|
|||
|
Brèves associées |
>>>
Billard d'Alhazen |
>>>
Octogone |
||
|
Pour en savoir plus |
>>>
Cercles et triangles équilatéraux >>>
Angles dans le cercle |
>>>
Cercle >>>
Triangle équilatéral |
||
Auteur de cette trouvaille: Jean-Louis
Breuil
225. Partitions des entiers avec 1 et 2 |
|
||
|
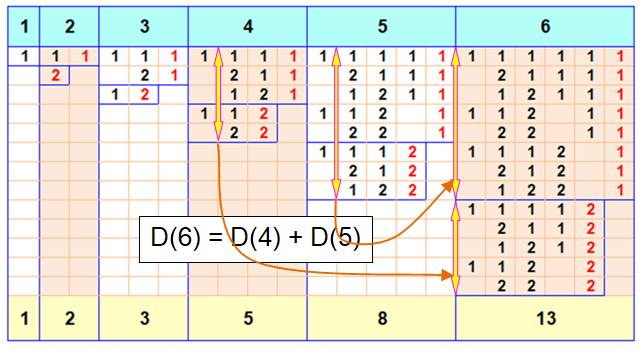
Ce tableau présente les compositions des nombres de 1 à 6: partitions avec autorisation des permutations. On se limite aux additions avec
les nombres 1 et 2 exclusivement. Voyez la construction: 1. Recopiez la composition précédente et ajoutez 1; 2. Recopiez la composition d'avant et ajoutez 2.
Lecture. colonne du 3, par exemple: 3 = 1 + 1 + 1 = 2 + 1 = 1 + 2 Pour le nombre 6: On retrouve toutes les compositions du 5 en ajoutant
1. Facile! Ensuite, pami toutes ces nouvelles combinaisons, il
est possible de remplacer les deux 1 finaux par un seul 2. Or, c'est la même
quantité que pour le 4 à laquelle on a ajouté 1 pour faire le 5, puis 1 pour
faire le 6. Soit la formule générale: D(n
+ 1) = D(n) + D(n–1) C'est typiquement la formule de récurrence de la
construction des nombres de Fibonacci. Les compositions avec les nombres de 1 à k se
calculent en utilisant les k-bonacci |
|||
|
Brèves associées |
>>>
Partitions et décompositions |
||
|
Pour en savoir plus |
>>>
Compositions avec 1 et 2 >>>
Partitions – Index |
>>>
Suite de Fibonacci >>>
Suites k-bonacci |
|
226. Pesée des quatre billes – Énigme |
|
|||
|
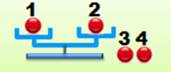
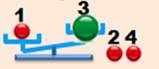
Énigme Vous
disposez de quatre billes absolument identiques visuellement. Une parmi
les quatre est plus lourde ou plus légère (ambivalence), sans que nous
sachions si c’est l’un ou l’autre. En deux pesées
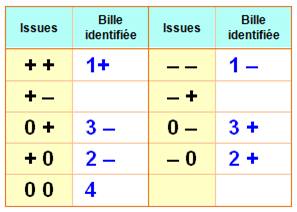
sur une balance à deux plateaux trouvez l'intrus et sa nature. Solution On effectue les deux pesées
indiquées et on note les résultats de pesées en plus, égal, moins (+ , 0 ,
–). La conclusion est à lire dans le tableau. Exemple de lecture du tableau En reprenant l'exemple, sur la troisième ligne à gauche: (0 +)
signifie équilibre et plateau gauche descend, alors la bille 3 est plus
légère (3–). Oups! Si on obtient deux fois l'équilibre, c'est la bille mise de côté (la 4
en dernière ligne) qui est fautive, mais on ne sait dire si elle est plus
lourde ou plus légère. |
Les deux pesées à effectuer
La bille 4 est
laissée de côté dans les deux pesées Sur cet exemple:
Notation: 0 + Tableau des conclusions en fonction
des résultats de pesée
|
|||
|
Brèves associées |
>>>
Énigme de la pesée des neuf billes |
>>>
Poules et oeufs >>> Énigme
des 30 euros |
||
|
Pour en savoir plus |
>>>
Énigme de la pesée des quatre billes – Explications >>>
Énigmes de pesées – Débutants et accès à tous les énigmes de pesées |
|||
227. Écart record entre premiers |
|
|||
|
L'écart (prime gap) entre les nombres premiers 317 et 331 est de 14. Il n'y a pas d'autres nombres premiers
entre les deux. Le théorème des nombres premiers
indique que l'écart moyen entre deux premiers consécutifs jusqu'à n est égal
à ln (n). Le mérite d'un écart entre premiers
est le rapport entre cet écart et l'écart moyen à ce niveau de nombres. Pour
le couple (314, 331) on a m = 14 / ln(314) = 2,43… Zhang a prouvé qu'il y une infinité d'écart plus petits que 70 000
000. En fait, asymptotiquement, 99% des premiers seraient suivi d'un premier
avec un écart de plus de 70 millions. |
En théorie, l'écart entre nombres premiers consécutifs peut être aussi
grand qu'on le souhaite! En effet:
C'est une autre chose que de les connaitre. La course au plus grand
écart est intense, et en 2017, le mérite connu dépasse 40. Record 2017 |
|||
|
Brèves associées |
>>> Nombres
2, 3, 5, 7, 11 … Premiers >>>
Premiers et cryptographie |
>>>
Algorithme de recherche |
||
|
Pour en savoir plus |
>>>
Écart entre nombres premiers >>>
Théorème des nombres premiers |
>>>
Nombres premiers – Introduction |
||
228. Énigme des quatre verres |
|
|||
|
Énigme Quatre verres sont disposés en carré sur un plateau tournant. Certains
sont à l'endroit et les autres à l'envers. Les yeux bandés, il vous est demandé de remettre tous les verres dans
le même sens en un minimum d'opérations. Une opération consiste à faire tourner le plateau. Vous prenez deux
verres et vous pouvez:
Un
observateur vous dit "FIN" si les verres sont tous dans le même
sens (ou fait sonner une cloche). |
Algorithme en cinq opérations 1) Mettre à l'endroit deux verres en diagonale; 2) Mettre à l'endroit deux verres adjacents; 3) Sur une diagonale, si l'un est à l'envers le retourner. FIN. Sinon,
en retourner un à l'envers. 4) Retourner deux verres adjacents 5) Retourner deux vers en diagonale |
|||
|
Brèves associées |
>>> Énigme du parking |
|||
|
Pour en savoir plus |
>>>
Énigme des quatre verres |
>>>
Jeux et énigmes – Index |
||
229. Théorie – Théorèmes – Axiomes |
|
|||
|
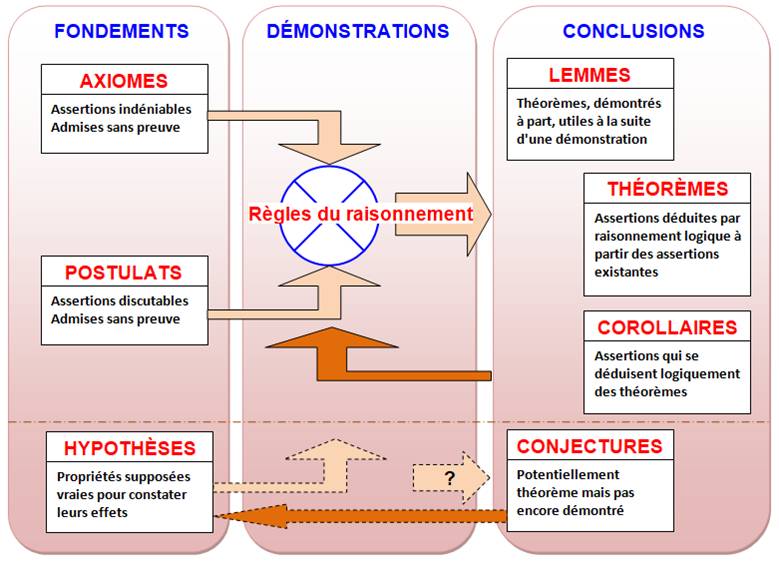
La géométrie que
nous apprenons en classe forme une théorie
mathématique. Il existe d'autres
géométries. Elle repose sur
des fondements constitués de:
En mathématique,
les affirmations, les vérités, les énoncés vrais … sont des assertions. Contraire de: hypothèses,
suppositions, allégations, conjectures … |
La théorie de la
géométrie est construite sur ces fondements et, via un raisonnement logique,
appelé démonstration, elle énonce des
vérités, appelées théorèmes ou parfois lemmes, s'il s'agit de théorèmes dans une étape
de démonstration. Parfois, une
vérité forte se révèle sans que la démonstration ait été trouvée, c'est une conjecture. En attente de preuve, la conjecture
peut être utilisée comme hypothèse pour poursuivre le raisonnent et déduire
de nouvelles conclusions qui deviendront théorèmes si la conjecture est
prouvée |
|||
|
|
||||
|
Brèves associées |
>>>
Ontologie des mathématiques |
|||
|
Pour en savoir plus |
>>>
Théorie – théorème – axiomes : développements |
|||
230. Factorielle |
|
|||
|
Factorielle n Le terme
"factorielle n", noté
n!, est un raccourci pour nommé le produit de n nombres consécutifs à
partir de 1.
Produit
de nombres consécutifs Le produit de k
nombres consécutifs est divisible par k! Ex: 7 . 8 . 9 = 504 = 6
x 84 = 3!
x 84 11.12.13.14.15
= 360 360 = 120 x 3003 Factorielle
somme La factorielle
d'une somme est divisible par le produit des factorielles des termes. Ex: (3 + 4)! = 1.2.3.4.5.6.7 est divisible par
(1.2.3)(1.2.3.4) = 3! . 4! Cette
propriété se démontre facilement: 1.2.3.4.5.6.7 = K . (1.2.3)(1.2.3.4)
? 5.6.7 = K .
1.2.3 = K . 3! C'est vrai en
application de la propriété précédente: le produit de trois nombres
consécutifs est divisible par 3! |
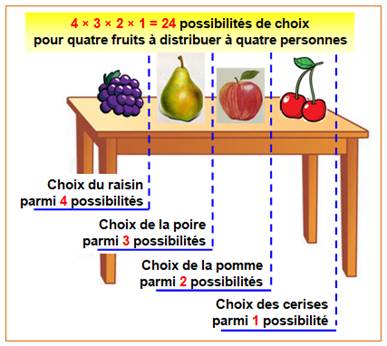
Dénombrer Chacun choisit
son fruit, l'un après l'autre. Il y a 24 possibilité de répartition.
Permutations La
quantité de permutations
de n objets est égale à factorielle n. Ex: (a,b,c), (a,c,b),
(b,a,c), (b,c,a), (c,a,b), (cb,a) |
|||
|
Brèves associées |
>>>
Factorielle 9 >>>
Factorielle et files indiennes |
>>>
Arrangements – Tiercé |
||
|
Pour en savoir plus |
>>>
Factorielle >>>
Produit de consécutifs |
>>>
Dénombrements >>>
Permutations |
||
231. Nombre à trouver |
|
|||
|
Exemple d'énigme Trouver un nombre comportant trois chiffres (de 0
à 9) tels que: Décodage Alors que A.B.C est le produit de trois nombres A,
B et C, le premier membre ABC représente un nombre à trois chiffres A, et C. Notations La multiplication se note X entre nombres,
parfois remplacé par un point. Elle se note par un point entre lettres et
souvent sans point lorsqu'il n'y pas de confusion possible. Recherche: le nombre est divisible par 5 et se termine par
0 ou 5. Seul 5 est valable, car 0 entrainerait un produit nul. En développant
l'égalité:
Premier membre impair => second membre impair
=> A et B impairs. Essais pour A = 1 => 21 + 2B = B => B = 7 Les autres (A = 3, 5, 7, 9) sont infructueux. Seule solution: 175 / 5 = 1 x 7 x 5 |
Nombre de Zuckerman
Notation [175, 5] 175 est égal à 5 fois le produit de ses chiffres Autres cas: Nombres de Zuckerman 72 pour k jusqu'à 100 et n jusqu'à 100 000. [36, 2], [15, 3], [24, 3], [384, 4], [175, 5], [12,
6], [735, 7], [128, 8], [672, 8], [135, 9], [144, 9], [1575, 9], [11, 11],
[1296, 12], [624, 13], [3276, 13], [224, 14], [816, 17], [216, 18], [432,
18], [34992, 18], [1197, 19], [12768, 19], [315, 21], [132, 22], [3168, 22],
[115, 23], [6624, 23], [8832, 23], [2916, 27], [1176, 28], [1344, 28], [3915,
29], [93744, 31], [51975, 33], [82944, 36], [1184, 37], [31488, 41], [77616,
44], [77175, 45], [4416, 46], [12288, 48], [1715, 49], [18816, 49], [612,
51], [312, 52], [212, 53], [112, 56], [1416, 59], [6144, 64], [6912, 64],
[4224, 66], [2144, 67], [35175, 67], [9315, 69], [13248, 69], [13824, 72],
[1332, 74], [28416, 74], [16632, 77], [33264, 77], [11664, 81], [23328, 81],
[13932, 86], [9612, 89], [89712, 89], [91728, 91], [2232, 93], [48128, 94],
[18432, 96], [21728, 97], [42336, 98] |
|||
|
Brèves associées |
>>> La somme des deux âges |
>>> Pesée des quatre billes |
||
|
Pour en savoir plus |
>>>
Nombre deviné – 175 >>>
Multiplication – Notations >>>
Nombres de Zuckerman |
>>>
Même question avec la somme ABC = k (A + B + C) |
||
232. Nombre sans facteur carré |
|
|||
|
Définition Un nombre carré est le produit de deux nombres
identiques. Un nombre avec facteur carré est un multiple d'un
nombre carré. Tous les autres sont sans facteurs carrés. Propriété Tout nombre se décompose en un produit de
facteurs uniques (théorème fondamental de l'arithmétique). Les facteurs d'un nombre sans facteur carré sont
tous uniques (sans puissance). |
Exemple
Liste jusqu'à 100 2, 3, 5, 6, 7, 10, 11, 13, 14, 15, 17, 19, 21,
22, 23, 26, 29, 30, 31, 33, 34, 35, 37, 38, 39, 41, 42, 43, 46, 47, 51, 53,
55, 57, 58, 59, 61, 62, 65, 66, 67, 69, 70, 71, 73, 74, 77, 78, 79, 82, 83,
85, 86, 87, 89, 91, 93, 94, 95, 97. |
|||
|
Brèves associées |
>>>
Diviseurs >>>
Nombres avec carrés, records |
>>>
Nombres de Fermat |
||
|
Pour en savoir plus |
>>>
Nombres sans facteurs carrés >>>
Théorème fondamental de l'arithmétique |
>>>
Nombres carrés >>>
Facteurs et diviseurs |
||
233. Pizza – Choix de la taille |
|
|||
|
Le choix Vous avez le choix entre une grande pizza de 46
cm ou deux petites pizzas de 30 cm. Vous en aurez plus en choisissant la 46. Cela
vous surprend ? Calcul des aires
|
Certains disent que ce qui est le meilleur c'est
la croûte. Alors, il est préférable de choisir les deux petites.
|
|||
|
Brèves associées |
>>>
Périmètre et aire |
|||
|
Pour en savoir plus |
>>>
Périmètre >>>
Périmètre – Curiosités >>>
Mon petit formulaire |
>>>
Aire >>>
Problèmes qui affolent le Net |
||
234. Deviner les nombres |
|
|||
|
Le tour de magie Le calculateur prodige Giacomo Inaudi savait
trouver en 30 secondes les quatre nombres consécutifs dont on donnait la
somme des carrés. Emploi d'une formule simple; mais encore fallait-il
savoir calculer une pseudo racine carrée (produit de deux nombres
consécutifs). Formule utilisée (n – 1)² + n² + (n + 1)² + (n +
2)² = 4n² + 4n + 6 = 4 n (n + 1) + 6 Avec cinq carrés (n – 2)² + (n – 1)² + n² + (n + 1)² + (n + 2)² = 5n² + 10 |
Exemple La somme des quatre carrés est 2 606. Calcul pour retrouver les 4 nombres Retirer 6: 2 600 Diviser par 4: 650 Produit de deux nombres consécutifs: 650 =
25 x 26 Nombres cherchés: 24, 25, 26, 27. En effet: 24² + 25² + 26² + 27² = 2 606 Encore plus facile avec 5 nombres On donne la somme: 3 135 Retirer 10 : 3 125 Diviser par 5: 625 Prendre la racine carrée: 25 Nombres cherchés: 23, 24, 25, 26, 27. En effet: 23² + 24² + 25² + 26² + 27² = 3 125 |
|||
|
Brèves associées |
>>>
Nombres deviné – Restes chinois |
|||
|
Pour en savoir plus |
>>>
Somme de carrés >>>
Somme de 3, 4, 5 … carrés |
>>>
Magie – Index
|
||
235. Angles dans trois carrés |
|
|||
|
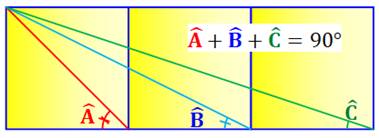
Défi Les trois angles dessinés dans ces trois carrés
totalisent 90°. Est-ce évident à démontrer ? |
|
|||
|
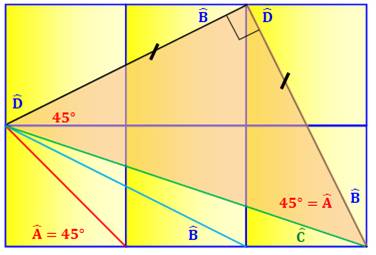
Démonstration quasi-muette Une duplication des carrés aide à réaliser une
démonstration simple. L'angle A est égal à 45° (diagonale du carré). Le triangle de couleur rose est isocèle
rectangle: isocèle car deux côtés égaux et rectangle car les angles B et D
(dont la somme est 90°), reportés à côté du sommet du triangle isocèle,
montrent que l'angle de ce sommet est égal à 90°. Or, dans ce type de triangle, les angles à la
base mesurent 45°. Dans le coin bas-droit de la figure, les trois
angles représentent bien A, B et C et leur somme vaut 90°. |
|
|||
|
Brèves associées |
>>> Pizza – Choix de
la taille |
>>> La
fourmi sur le cube |
||
|
Pour en savoir plus |
>>>
Angles et trois carrés |
>>>
Triangle isocèle rectangle |
||
236. Nombres de Proth et de Sierpinski |
|
|||
|
Nombres de Proth: nombres de la forme: Certains critères permettent de détecter s'ils
sont premiers ou composés. Nombre de Sierpinski: valeur de k dans un nombre de Proth tels que N
n'est jamais premier quelle que soit la valeur de n. On ne sait pas encore de manière certaine quel
est le plus petit. En début 2019, cinq nombres inférieurs au plus petit connu
résistent encore aux tests car très grands. Ils étaient 17 au début de ce
siècle. |
Plus grand nombre de Proth premier
connu 10 223 x
2311721165 + 1 C'est le neuvième plus grand premier connu en début 2019. Plus petits nombres de Sierpinski 78 557 est le plus petit connu. 271 129 est le deuxième plus petit connu et le plus petit
premier connu. |
|||
|
Brèves associées |
>>>
Nombres de Fermat |
>>> Nombres sans facteur carré |
||
|
Pour en savoir plus |
>>>
Nombres de Sierpinski |
>>>
Nombres en Puissances de 2 |
||
237. Multiplication rapide à pivot |
|
|||
|
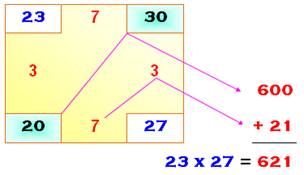
La méthode est illustrée par un exemple: 23 x 27. On choisit un nombre "facile" proche
des deux nombres à multiplier. Disons 20. Les écarts sont 3 et 7 (en rouge) Le produit se calcule simplement en multipliant
les deux nombres aux coins en vert (20 x 30 = 600) et en lui ajoutant le
produit des nombres en rouge (3 x 7 = 21). Bilan: 23 x 27 = 600 21 = 621. |
|
|||
|
Brèves associées |
>>> Multiplication de nombres entiers >>>
Multiplication rapide |
>>> Multiplication par 111 |
||
|
Pour en savoir plus |
>>>
Multiplications mentales rapides |
>>>
Calcul mental – Index |
||
238. Divisibilité par 11 |
|
|||
|
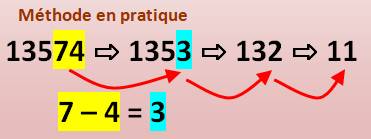
Pour savoir si un nombre est divisible par 11:
|
|
|||
|
Brèves associées |
>>> Divisibilité de 123456789 – Critères |
>>> Divisibilité du produit de nombres |
||
|
Pour en savoir plus |
>>>
Divisibilité par 11 |
>>>
Calcul mental – Index |
||
239. 7 parmi 15: combien de possibilités ? |
|
||||
|
On cherche des quantités de combinaisons. Par
exemple: deux objets parmi quatre ou cinq parmi quinze. Exemple simple Sélection de deux nombres parmi quatre (1, 2, 3,
4): 12, 13, 14, 23, 24,
34 On calcule:
On retrouve le 4 et le 2, et deux
nombres en haut et en bas. Avec sept nombres parmi 15 On met 15 en tête suivi de sept nombres en haut, puis 7
suivi de sept nombres en bas.
|
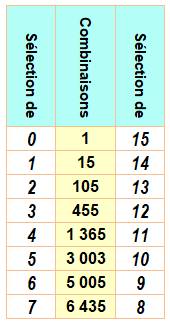
Sélection de 1 à 15 parmi 15 Ce tableau montre toutes les
possibilités de choix de 0 à 15 nombres parmi 15. Remarquez la symétrie:
autant de combinaisons de 7 parmi 15 que de 8 parmi 15, par exemple. Probabilité de tirer une
combinaison de sept nombres donnés C'est l'inverse des nombres
affichés. Probabilité de tirer une combinaison de sept nombres parmi quinze:
|
|
|||
|
Brèves associées |
>>> Jeu de
dés |
>>>
Anniversaire le même jour |
|||
|
Pour en savoir plus |
>>>
Combinaisons >>>
Application au LOTO |
>>>
Dénombrement – Index |
|||
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()