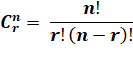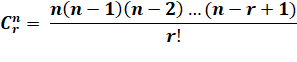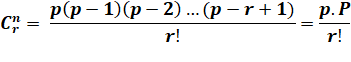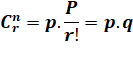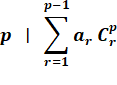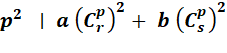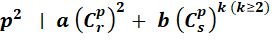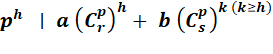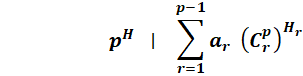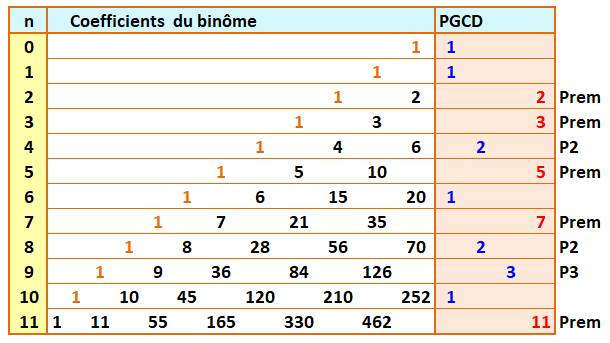
Divisibilité des coefficients du triangle de Pascal

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 10/01/2024 Orientation générale DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	ITÉRATIONS
Débutants Général	TRIANGLE de PASCAL				Glossaire Général
INDEX Itérations	Approche	Formules	Propriétés	Historique
	Triangle	Valeurs	Fractal	Puissance 11
		Binôme	Divisibilité
		Sommaire de cette page >>> Rappels – Boite à outils >>> Divisibilité >>> Généralisation – Triangle >>> Forme polynomiale >>> Combinaisons linéaires

TRIANGLE de PASCAL

Divisibilité des coefficients

Tous les nombres d'une ligne, sauf les deux extrémités (égales à 1), sont divisibles par le numéro de ligne chaque fois que ce numéro est un nombre premier. Cette propriété s'étend aux lignes suivantes selon un effet de dominos. Les nombres concernés forment un dessin en triangle rectangle.
Les nombres du triangle de Pascal sont aussi les coefficients du développement du binôme.

Rappels – Boite à outils
Les coefficients du triangle de Pascal et sont également ceux du développement du binôme à une certaine puissance. Ce sont aussi la quantité de combinaisons de r objets parmi n.	Triangle de Pascal Ligne n°2: 1 2 1 Ligne n°3: 1 3 3 1 Ligne n°4: 1 4 6 4 1 … Binôme en puissance (x + y)² = x² + 2xy + y² (x + y)³ = x³ + 3x²y + 3xy² + y³ (x + y)⁴ = x⁴ + 4x³y + 6x²y² + 4xy³ + y⁴ …
Chaque coefficient est donné par cette formule: n est le numéro de la ligne et r le rang dans la ligne. Le point d'exclamation signifie: factoriel. Voir Symboles	Formule compacte Formule développée
Théorème fondamental de l'arithmétique:	Tout nombre est le produit unique de nombres premiers croissants.
Lemme d'Euclide: a, b et c étant des entiers avec a et b premiers entre eux:	Si a divise bc, alors a divise c ou encore: Si bc/a est un nombre entier, alors a divise c.

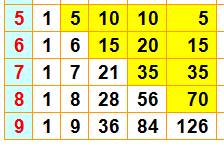
Divisibilité des coefficients binomiaux
Soit, par exemple, la cinquième ligne du triangle de Pascal. Hormis les extrémités, tous les coefficients sont divisibles par 5, nombre qui est le numéro de la ligne. Cette propriété se retrouve pour toutes les lignes dont le numéro est un nombre premier.	Cinquième ligne divisible par 5 1 5 10 10 5 1 Septième ligne divisible par 7 1 7 21 35 35 21 7 1
Baptême des lignes et du rang dans la ligne. Notez que nous nous intéressons aux coefficients des rangs r = 1 à r = n – 1. Soit r toujours inférieur à n.
Démonstration
Chaque coefficient pour une ligne de rang premier s'écrit:
Or, le coefficient est un nombre entier, alors le dénominateur divise le numérateur.	r! divise exactement le numérateur.
Nous savons que r est inférieur à p (Voir ci-dessus, baptême).	Tous les facteurs de r! sont inférieurs à p (nombre premier). Ce qui veut dire que p et r! sont premiers entre eux.
Lemme d'Euclide	r! et p sont premiers entre eux. Or r! divise p.P, il divise donc P.
Le coefficient du binôme est de la forme:
Conclusion pour les coefficients des rangs r = 1 à r = p – 1.	Tous les coefficients C sont divisibles par le numéro de la ligne p.

Théorème

Sur toutes les lignes du triangle de Pascal dont les numéros sont des nombres premiers, les coefficients hormis les unités aux extrémités, sont divisible par le numéro de la ligne.

Le PGCD des coefficients du binôme de la ligne n, hors les 1 des extrémités, est égal à n si n est premier et sinon à 2 pour les puissances pures et 1 pour les autres.

Notez que si n est premier, les coefficients sont des multiples de n. Car le n du numérateur n'est jamais divisible par les nombres au dénominateur.

Exemple:

Illustration

Voir Brève 56-1118 / Divisibilité par 7 de puissances 7 et généralisation

Généralisation – Triangle divisible par p
Observons la ligne 5 et les suivantes et repérons les nombres divisibles par 5. Même chose avec 7. Une forme générale en triangle rectangles se dessine. Oui! C'est vrai pour toute ligne de rang premier. Remarquons tout de suite que: Par exemple, 28 = 7 + 21, somme des deux nombres de la ligne du dessus; nombres qui, chacun, sont divisibles par 7. Pas étonnant que 28 = 7 + 21 soit lui aussi divisible par 7.	Triangle des divisibles par 5 Triangle des divisibles par 7
Formulation:	Soit n tous les nombres entiers de 1 à p – 1. Alors pour tout r = n+1, n+2 … p-1,

Démonstration
Pour n = 0, on retrouve:	Le théorème vu ci-dessus qui dit que les coefficients, sauf les extrémités, sont divisibles par p.
Pour les lignes suivantes:	Lorsque ces coefficients, somme des deux du dessus sont eux-mêmes divisibles par p, alors leur somme est aussi divisible par p.

Théorème

Soit une ligne du triangle de Pascal dont le numéro est un nombre premier (hormis les unités aux extrémités), puis la ligne suivante sauf son coefficient de gauche et ainsi de suite jusqu'à épuisement, tous ces nombres sont divisibles par le numéro de la ligne initiale.

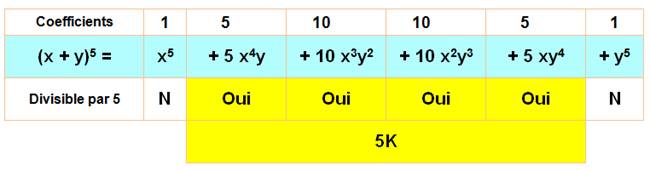
Divisibilité d'une forme polynomiale
Nous savons que sur une ligne de numéro premier p, tous les coefficients sont divisibles par p, sauf les deux aux extrémités. Par exemple avec la ligne 5:
Dans le développement, il suffit de retirer les extrémités pour obtenir un polynôme divisible par p.	(x + y)⁵ – (x⁵ + y⁵) = 5 K est divisible par 5.
Cette remarque est généralisable à toutes les lignes de numéros premiers	(x + y)^p – (x^p + y^p) = p K est divisible par p.
En conservant, cette fois, les extrémités:	x^p + y^p = (x + y)^p – p K
En prenant le cas où p divise la somme x + y, le quotient étant H.	x^p + y^p = (p H)^p – p K
À droite, les deux termes sont divisibles par p, le membre de gauche est divisible par p.	Si p (premier) divise x + y, alors p divise x^p + y^p.

Théorèmes

(x + y)^p – (x^p + y^p) est divisible par p (premier).

x^p + y^p est divisible par p si x + y l'est.

Voir Autres formes polynomiales

Puissance de 2
Pour x = y = 1, ces expressions sont divisibles par p (premier):	(1 + 1)^p – (1^p + 1^p) 2^p – 2 2 (2^{p – 1} – 1)
Dans le cas où p est premier supérieur à 2:	2^{p – 1} – 1 est divisible par p.
C'est un cas particulier du petit théorème de Fermat pour a = 2, qui s'énonce:	a^{p – 1} – 1 est divisible par p. pour tout a non divisible par p.
La réciproque n'est pas vraie!	Si 2^{n – 1} – 1 est divisible par n, n n'est pas forcément premier, mais pseudo-premier. Premier cas qui le prouve: n = 341

Combinaisons linéaires
Évidemment une combinaison linéaire des coefficients d'une ligne première est divisible par p puisque chaque coefficient l'est. La barre verticale se lit: divise	Combinaisons linéaires de deux coefficients Divisibilité d'une combinaison linéaire de tous les coefficients de la ligne
Généralisation avec les coefficients portés à une certaine puissance. Avec p est premier et r = {1,2 … p–1}. Les formules, données avec deux termes, sont généralisables à n termes.	Avec le carré Avec un carré au minimum Avec une puissance minimale h

Théorème

C_r^psont les coefficients du triangle de Pascal situés sur la ligne numéro p, avec p premier. a_r sont des entiers; H_r des entiers positifs dont H est le plus petit.

Suite	Triangle de Pascal – Formules
Voir	Combinaisons Formule du binôme Petit théorème de Fermat
Aussi	Boucle infernale Calcul mental Géométrie – Index Récurrence Théorie des nombres
Graphes	Graphes et chemins optimums Parcours des abeilles Voyageur de commerce
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Iteration/TrgPascD.htm