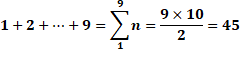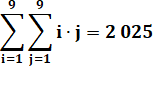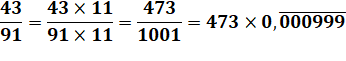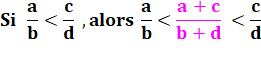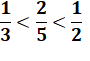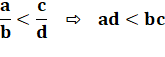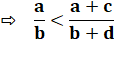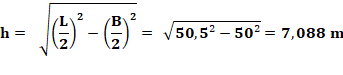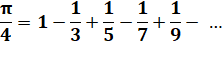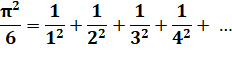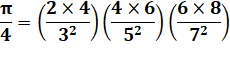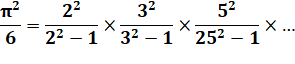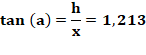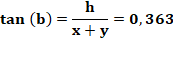NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 03/10/2024 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 10		Page 20		Page 30		Page 40			Page 50

	Page 20 (380-399)		Page 21 (400-419)		Page 22 (420-439)		Page 23 (440-459)		Page 24 (460-479)
	Page 25 (480-499)		Page 26 (500-519)		Page 27 (520-539)		Page 28 (540-559)		Page 29 (560-579)

BRÈVES de MATHS – Page 29

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

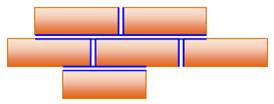
560. Les six briques
Énigme Sachant que le périmètre d'un seul rectangle est égal à 100, quel est le périmètre du dessin ? Solution Lé périmètre des six briques est égal à: 6 x 100 = 600. En écartant légèrement les briques, on constate que les traits en bleu ne font pas partie du périmètre du dessin. On dénombre six longueurs de briques et six largeurs, couvrant donc trois périmètres, soit: 300. Le périmètre du dessin est donc: 600 – 300 = 300.
Brèves associées	>>> Carrés et dominos	>>> Château et douves
Pour en savoir plus	>>> Périmètres avec des rectangles	>>> Jeux et énigmes – Index

561. Mêmes chiffres en base b
Cas où le nombre et sa conversion en base b présentent les mêmes chiffres. Ces motifs sont très nombreux. Le plus petit: 13₁₀ = 31₄En effet: 13 = 3 x 4 + 1 Autre exemple: 9 730₁₀ = 3 790₁₄ En effet: 3x14³ + 7x14² + 9x14 + 0 = 8 232 + 1 372 + 126 = 9 730		Exemple typique 100 + 50 + 8 = 81 + 72 + 5 Exemple avec 10 nombres consécutifs 9 730₁₀ = 3 790₁₄ 9 731₁₀ = 3 791₁₄ … 9 739₁₀ = 3 799₁₄
Brèves associées	>>> Conversion en binaire		>>> Brèves Numération – Index
Pour en savoir plus	>>> Mêmes chiffres en base b		>>> Nombre 158

562. Nombre différence de carrés
Nombres impairs Tout nombre impair (n = 2k + 1) est la différence de deux carrés successifs: n = (k + 1)² – k². Exemple 11 = 5 x 2 + 1 = 6² – 5². Notez que 6 + 5 = 11 et 6 – 5 = 1; le produit 1 x 11 est égal à 11. 91 = 45 x 2 + 1 = 46² – 45². Avec 46 + 45 = 91 et 46 – 45 = 1; le produit 1 x 91 est égal à 91.		Tout nombre Tout nombre est égal à, au moins, une différence de carrés, sauf, les nombres en 4k + 2 et les nombres 1, 2, 4. Exemple 96 = 25² – 23² = 14² – 10² = 11² – 5² = 10² – 2² Le nombre 96 est quatre fois différences de carrés. Notez que la somme et la différence de ces couples sont des diviseurs de 96. Ex: 25 + 23 = 48 et 25 – 23 = 2 => 48 x 2 = 96 14 + 10 = 24 et 14 – 10 = 4 => 24 x 4 = 96
Brèves associées	>>> Somme de puissances >>> Multiples de 4		>>> Brèves Puissances – Index
Pour en savoir plus	>>> Nombres, différence de carrés >>> Différence de carrés – Record de cas		>>> Nombre 96

563. Nombres d'or et d'argent
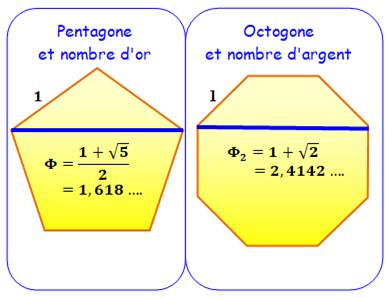
Le nombre d'or et le nombre d'argent sont les longueurs des diagonales du pentagone et de l'octogone respectivement. Ces deux nombres sont la limite du rapport entre deux nombres successifs de Fibonacci ou de Pell-Lucas. La suite de Fibonacci est telle que chaque nombre est la somme des deux précédents en commençant par 1, 1. La suite de Pell-Lucas est telle que chaque nombre est la somme de deux fois le précédent et une fois son précédent en commençant par 1, 2.
Brèves associées	>>> Nombres géométriques	>>> Brèves Nombres – Index
Pour en savoir plus	>>> Suite de Fibonacci et cousines	>>> Pentagone >>> Octogone

564. Polygones rigides
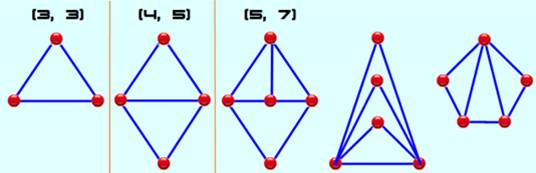
Rendre rigide un polygone consiste à créer des triangles, seuls polygones rigides naturellement. L'invariant des structures rigides est satisfait: 2P – A = 3 Exemple pour le pentagone: P = 5 points (ou sommets) A = 7 arêtes 2P – A = 10 – 7 = 3.		Il existe une seule forme de triangle rigide, comme pour le quadrilatère. Avec le pentagone, il y en trois, pour l'hexagone 13 et la quantité augmente très rapidement.
Brèves associées	>>> Pentagone rigide façon meccano		>>> Brèves constructions – Index
Pour en savoir plus	>>> Polygones rigides		>>> Polygones – Introduction et index

565. Somme de la table de multiplication
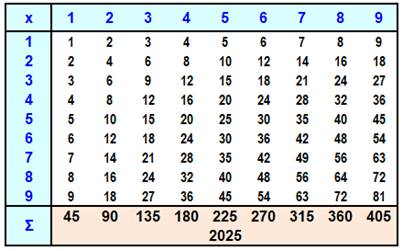
Problème Quelle est la somme de tous les nombres figurant dans la table de multiplication des nombres de 1 à 9 ? Solution On remarque que la somme de la première colonne est celle des nombres de 1 à 9 qui est égale à: Chaque des colonnes montre les mêmes nombres multipliés par 2, 3, … 9. La somme sera: 45 x (1 + 2 + ... + 9) = 45 x 45 = 2 025 Formulation		Table de multiplication Somme des nombres de la table 1 à 9 = 45² = 2 025 Somme des nombres de la table 1 à 10 = 55² = 3 025
Brèves associées	>>> Somme: 1 + 2 + 3 + 4 + …		>>> Brèves Calculs – Index
Pour en savoir plus	>>> Table de multiplication		>>> Nombre 2 025 >>> Nombre 3 025

566. Somme des impairs

Démonstration muette de cette propriété:

La somme des k premiers impairs est égale à k².

1 + 3 =

1 + 3 + 5 =

1 + 3 + 5 + 7 =

1 + 3 + 5 + 7 + 9 =

1 + 3 + 5 + 7 + 9 + 11 =

4 = 2²

9 = 3²

16 = 4²

25 = 5²

36 = 6²

Brèves associées

>>> Somme des carrés des entiers

>>> Brèves Calculs – Index

Pour en savoir plus

>>> Somme des nombres impairs

>>> Carrés

567. Impairs, carrés et cubes

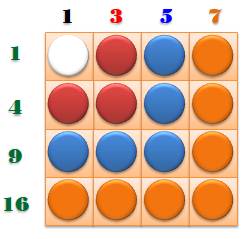
La somme des impairs pris par quantité croissante k donne lieu à un cube égal à k³.

La somme cumulée de ces cubes est un carré.

La somme des impairs consécutifs par tranche est un cube.

La somme de tous les impairs consécutifs est un carré.

1	= 1	= 1³	1	= 1²
3 + 5	= 8	= 2³	9	= 3²
7 + 9 + 11	= 27	= 3³	36	= 6²
13 + 15 + 17 + 19	= 64	= 4³	100	= 10²
21 + 23 + 25 + 27 + 29	= 125	= 5³	225	= 15²

Brèves associées

>>> Caractérisation des carrés

>>> Brèves Calculs – Index

Pour en savoir plus

>>> Somme impairs = cubes

>>> Entiers impairs et cubes

568. Division rapide par 91
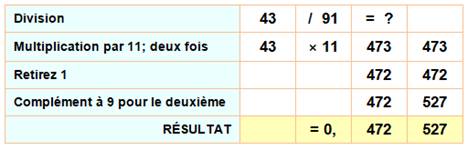
Diviser un nombre à deux chiffres par 91 est particulièrement simple. On commence par multiplier par 11, et …Voir l'exemple.
Explication		Méthode basée sur cette prorpiété: 91 x 11 = 1001. On peut mettre la division sous cette forme: Le calcul de la période
Au-delà de 91		Si le nombre à diviser dépasse 91, ajouter la quantité de fois que ce nombre contient 91. De n = 91 à 182, ajoutez 1.
Brèves associées	>>> Multiplication rapide		>>> Brèves Calcul mental – Index
Pour en savoir plus	>>> Divisibilité par 91		>>> Nombre 91

569. La suite qui se lit
Suite de nombres dite du commentaire numérique ou suite de Conway. Suite de nombres comportant une autoréférence. Elle mixte nombres et quantité de nombres. Objet fréquent d'une énigme.		1 11 *– Je vois un 1 sur la ligne du dessus, j'écris 11* 21 – Cette fois, il y deux 1, j'écris 21 1211 – Je vois un 2 et un 1 sur la ligne du dessus, j'écris 1211 111221 – J'ai compris: un 1, un 2 et deux 1 312211 – Etc. 13112221 1113213211 31131211131221 13211311123113112211 11131221133112132113212221 3113112221232112111312211312113211 …
Brèves associées	>>> La suite qui se lit (explication)		>>> Brèves Énigmes – Index
Pour en savoir plus	>>> Commentaire numérique		>>> Énigmes – Index

570. Triangle de Pascal – Propriétés
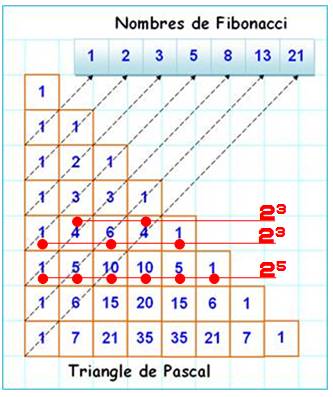
On sait que chaque nombre est égal à la somme de celui du dessus et de celui dessus à gauche: 3 + 2 + 1 ou encore 35 = 20 + 15. La somme des nombres sur la ligne n est égale à 2ⁿ : 1 + 5 + 10 + 10 + 5 + 1 = 32 = 2⁵ La somme des nombres un sur deux sur la même ligne est égale à 2^n-1. Et, cela deux fois. La somme des nombres le long des diagonales produit les nombres de Fibonaci.
Brèves associées	>>> Triangle de Pascal	>>> Brèves Dénombrement – Index
Pour en savoir plus	>>> Triangle de Pascal	>>> Nombres de Fibonacci

571. Fraction médiane
Propriété Avec deux fractions, l'une plus petite que l'autre, il est toujours possible de trouver une fraction intermédiaire, la fraction médiane. Exemple En effet: 0,333… < 0,4 < 0,5		Démonstration a/b < c/d avec des nombres positifs (au moins b et d). Alors: ad + ab = bc + ab a(b + d) < b(a + c) Idem pour l'autre inégalité.
Brèves associées	>>> Fraction – Construction géométrique		>>> Brèves Opérations – Index
Pour en savoir plus	>>> Fraction médiane		>>> Fraction

572. Échiquier et dominos
Énigme Peut-on couvrir cet échiquier tronqué de deux cases de même couleur avec des dominos ? Réponse: NON ! Démonstration Quantité de cases sur l'échiquier tronqué: 32 cases noires et 30 cases blanches. Avec 62 cases à couvrir il faut 31 dominos. On remarque qu'un domino couvre toujours une case blanche et une case noire quelle que soit sa position. Donc, les 31 dominos couvriront 31 cases blanches et 31 cases noires et jamais 32 et 30 comme requis.		Illustration Les deux cases blanches des côtés opposés ont été retirées.
Brèves associées	>>> Tétris et pavage		>>> Brèves Énigmes – Index
Pour en savoir plus	>>> Problème de l'échiquier tronqué		>>> Dominos

573. Cubes et carré de sommes
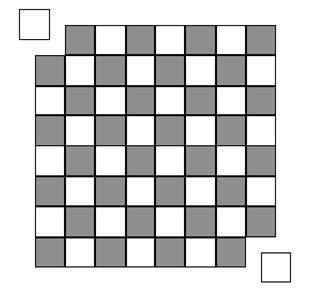
Tous les cubes présentent le même jeu de relations que le cube de 6. Il est plus facile de constater les relations que de les exprimer toutes. La relation principale (en dernière ligne) dit que: La somme des premiers cubes est égale au carré de la somme des mêmes nombres. Cette relation se prolonge pour la somme de k cubes consécutifs comme étant la différence entre carrés de deux suites de nombres consécutifs.
Brèves associées	>>> Belle égalité entre carrés et cubes >>> Carré = somme de cubes	>>> Brèves Relations – Index
Pour en savoir plus	>>> Carré = somme de cubes >>> Nombre 216	>>> Carrés >>> Cubes

574. Triangle – Périmètre minimum
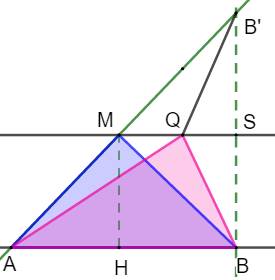
Question Deux droites parallèles. Un segment AB formant la base de deux triangles ayant M et Q pour sommets. Quel est le triangle qui a le plus petit périmètre ? Réponse C'est le triangle isocèle AMB qui a le plus petit périmètre. Pourquoi ? Dessiner le point B' symétrique de B par rapport à la parallèle MQ. MS est la médiatrice de BB': QB =QB’ Périmètres: P_AMB = AM + MB + BA = AB' + AB P_AQB = AQ + QB + BA = AQ + QB' + AB Or, dans le triangle AQB': AB' < AQ + QB' Lorsque le point Q se rapproche de M, le périmètre diminue. Il est minimum lorsque Q = M; le triangle est alors isocèle.
Brèves associées	>>> Triangle – Partage en six parts égales	>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Triangle – Périmètre minimum >>> Inégalité triangulaire	>>> Triangles – Index

575. Corde tendue
Question Terrain de 100 m et corde de 101 m. Hauteur h du piquet pour que la corde soit tendue ? Réponse Simple, avec le théorème de Pythagore.		Avec une corde de 101 m pour une distance de 100 m, la hauteur h dépasse les 7 m.
Brèves associées	>>> Corde à l'Équateur – Paradoxe		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Corde tendue et paradoxe du cercle		>>> Théorème de Pythagore

576. Pi en somme et produit
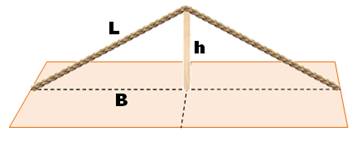
Somme Formule de Leibniz (1646-1716) Formule d'Euler (1707-1783)		Produit Formule de Wallis (1616-1703) Formule de Riemann (1826-1866)
Brèves associées	>>> Constante PI et le cercle		>>> Brèves Nombres – Index
Pour en savoir plus	>>> Formules pour Pi		>>> Constante Pi – Index

577. Hauteur du donjon

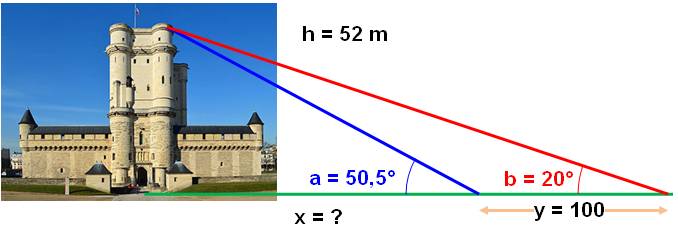
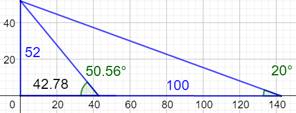
Défi

Sans accès au pied du donjon, comment estimer la hauteur du donjon du château de Vincennes ? La valeur donnée dans les livres est 52 m.

Mesures

Placé en un certain point, je mesure un angle b = 20°.

En avançant de 100 m, l'angle passe à 50,5°

Ai-je assez de données ? Oui !

Une modélisation avec GeoGebra confirme le calcul

Calcul

Hauteur du donjon	h
Avec l'ange a
Avec l'ange b
Avec h en commun	1,213x = 0,303(x+100)
Résolution en x	x = 42,87
Calcul de h	h = 1,213 x 42,87 = 51,05 m

Note: le résultat est très dépendant de

la précision de mesure des deux angles.

Brèves associées

>>> Mesurer les triangles – Trigonométrie

>>> Brèves Trigo – Index

Pour en savoir plus

>>> Hauteur du donjon

>>> Résolution des triangles

>>> Tangente

>>> Trigonométrie – Index

578. Chemin le plus court
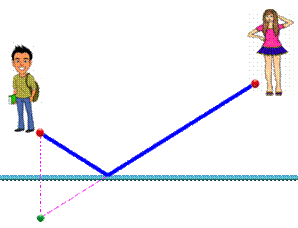
Alexis se propose d'amener un livre à Pauline. Il doit cependant s'approcher du tapis roulant pour y déposer son sac à dos. Quel est le chemin le plus court ? Si Alexis se trouvait de l'autre côté, à la même distance du tapis (position symétrique), il irait tout droit. Notons le point où il aurait déposé son sac. Alexis doit alors rejoindre le point de dépôt du sac et se diriger vers Pauline. Évidemment, on aurait le même chemin en prenant la position symétrique de Pauline. On trouve d'autres exemples comme la vache ou la chèvre qui va boire à la rivière avant de rentrer à la ferme, ou encore, le petit-fils qui apporte un seau d'eau à sa grand-mère.
Brèves associées	>>> Ponts de Königsberg	>>> Brèves Graphes – Index
Pour en savoir plus	>>> Trajets les plus courts	>>> Symétrie

579. Nombres cachés dans notre langue

Mots de français dont l'étymologie renferme un nombre caché d'une origine quelconque.

Soit, le nombre est d'origine étrangère et il est difficilement reconnaissable comme dans punch (5 en hindi);

Soit, le nombre est d'origine française et la déformation le rend méconnaissable comme dans tête-bêche qui vient de tête en béchevet (en double chevet).

On exclut les nombres à préfixes explicites comme bi-, tri-, etc. On les retrouve tous dans les pages culture des nombres.

*1/10*	Décimer
1	Unique
2	Biscuit
2	Brouette
2	Besace
2	Tête-bêche
3	Sampan
3	Treillis
4	Carillon
5	Punch
5	Lustre (5 ans)
5	Quentin
7	Semaine
7	Septentrional
9	Noon (lune en anglais)
12	Duodénum
20	Score
20	Hussard
50	Khamsim (vent)
*100*	Hécatombe
*144*	Grosse (12²)
*10 000*	Myriade
*10 000*	Banzaï (10 000 ans)

Brèves associées

>>> Notion de "2" cachée

>>> Brèves Langue – Index

Pour en savoir plus

>>> Nombres et culture

>>> Linguistique – Index

Retour	Brèves de maths – Page 28
Suite	Brèves de maths – Page 30
Voir	Voir liens en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve29.htm

560. Les six briques

561. Mêmes chiffres en base b

562. Nombre différence de carrés

563. Nombres d'or et d'argent

564. Polygones rigides

565. Somme de la table de multiplication

566. Somme des impairs

567. Impairs, carrés et cubes

568. Division rapide par 91

569. La suite qui se lit

570. Triangle de Pascal – Propriétés

571. Fraction médiane

572. Échiquier et dominos

573. Cubes et carré de sommes

574. Triangle – Périmètre minimum

575. Corde tendue

576. Pi en somme et produit

577. Hauteur du donjon

578. Chemin le plus court

579. Nombres cachés dans notre langue