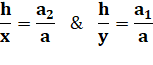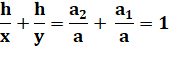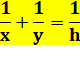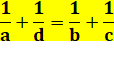Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 02/11/2023 M'écrire Brèves de Maths

INDEX Géométrie Défis géométriques Jeux et énigmes	Problèmes de longueurs
	Échelles	Puits	Bassin

Faites un double-clic pour un retour en haut de page

Théorème de la double échelle Théorème des quatre échelles Déterminer le point de croisement de deux demi-droites obliques reposant sur deux murs verticaux se faisant face, à la façon de deux échelles.
	Sommaire de cette page >>> Croisement de barres obliques >>> Théorème de Stengel >>> Milieu de l'échelle sur un mur >>> Deux échelles sur murs	Débutants Géométrie Glossaire Géométrie

Croisement de barres obliques		haut
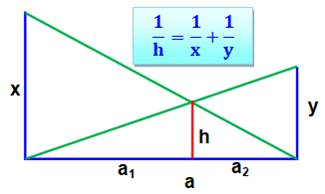
Deux barres obliques (Cross ladder theorem) Deux parois parallèles (verticales ou non) de hauteur x et y. Deux segments verts. Hauteur h ? Propriété Théorème de Thalès Somme Division par h	Théorème de la double échelle Propriété vraie quelle que soit la longueur a. Vraie aussi si les murs sont obliques, mais restant parallèles. Voir Moyenne harmonique (air de famille)
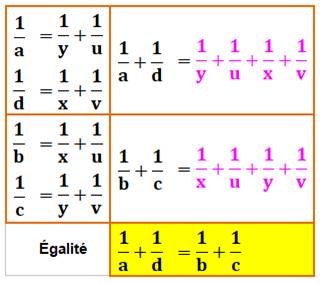
Quatre barres obliques (Double cross ladder theorem) Deux parois verticales de hauteur x et y. Quatre barres droites vertes rejoignant les points d'altitude x, y u et v. Relation entre les altitudes de croisement a, b, c, et d ? Propriété En appliquant le théorème des "échelles croisées"	Théorème des quatre échelles

Voir Brève 37-727 / Brève 55-1085

Illustrations

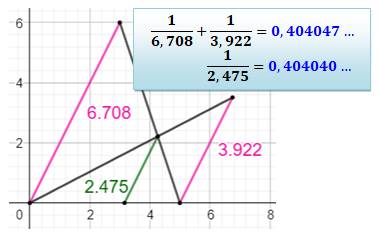
Cas de droites obliques

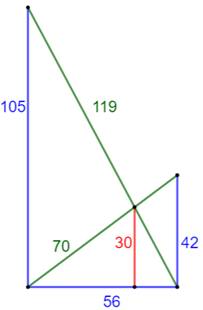
Solution en nombres entiers

Théorème de Stengel		haut
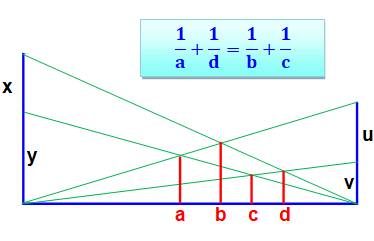
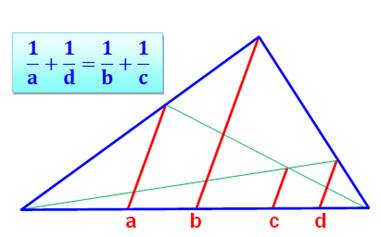
Construction Un triangle quelconque. Deux segments (verts) issus de deux sommets Quatre segments parallèles a, b, c et d (rouges). Théorème

Milieu de l'échelle sur un mur		haut
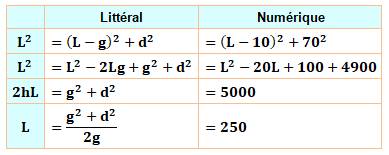
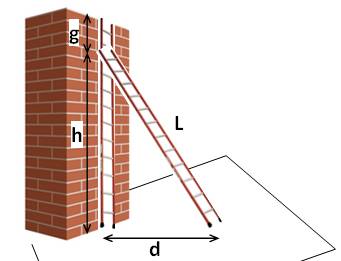
Construction Un mur et une échelle de longueur L. Penchée, elle descend d'une longueur g et elle s'écarte du mur d'une longueur d. On connait d = 70 et g = 10, quelle est la longueur de l'échelle Calculs (application du théorème de Pythagore)
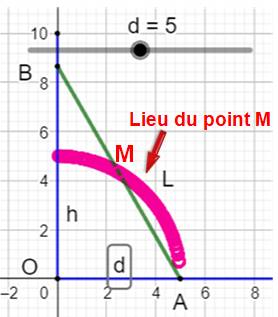
Milieu de l'échelle Quel est le lieu du milieu de l'échelle en fonction de d ? Le dessin GeoGebra montre qu'il s'agit d'un quart de cercle Piste On note que l'abscisse du point M vaut la moitié de d. On calcule l'ordonnée avec le théorème de Pythagore.

Deux échelles sur murs		haut
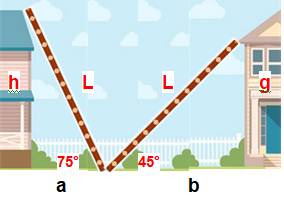
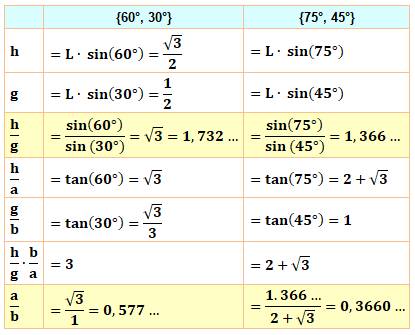
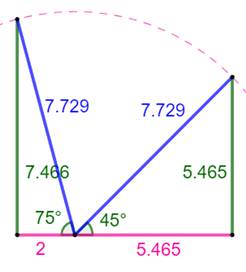
Construction Deux maisons et deux échelles de même longueur posées sur le sol au même endroit et rejoignant le toit de chaque maison avec des angles de (60° et 30°) et aussi (75° et 45°). Relations entre les longueurs: h et g et entre a et b ? Calculs Exemple numérique (75°, 45°; voir figure) h / g = 7,466 / 5,465 = 1,366 … a / b = 2 / 5,465 = 0,366 …	Cas des angles (75°, 45°) Exemple numérique Quelle que soit la distance au sol, les deux angles donnés imposent un rapport constant entre les segments verts tout comme entre les segments roses.

Haut de page (ou double-clic)

Retour	Énigme du puits
Suite	Énigme du tirebouchon Carré Carré parfait
Voir	Géométrie – index Jeux – index Traversée de la rivière
Sites	Problème des deux échelles – Wikipédia Crossed Ladders Theorem – Wolfram MathWorld Double cross ladder Theorem – Relish Maths – Vidéo A litany of ladders: easy problems with hard solutions – Alasdair McAndrew
Cette page	http://villemin.gerard.free.fr/Geometri/Echelle.htm