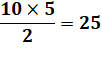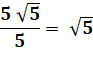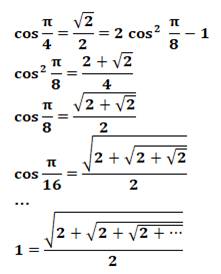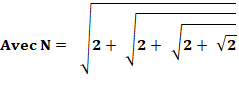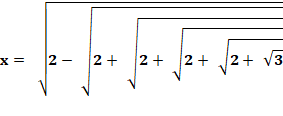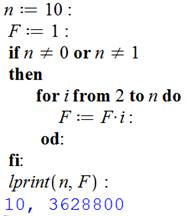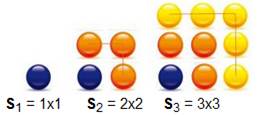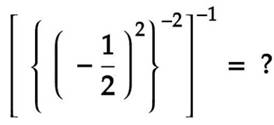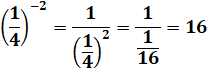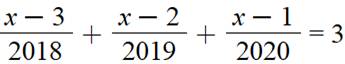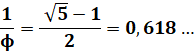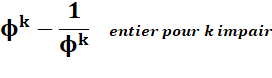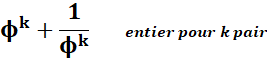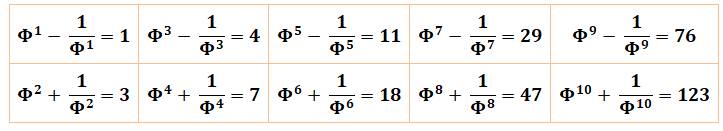|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
BRÈVES de MATHS – Page 34 Un millier de faits et chiffres sur les nombres et les
mathématiques
En principe ces pages sont très abordables sans
connaissances particulières de maths. Elles sont proposées dans un ordre
quelconque favorisant la découverte de sujets multiples. |
Anglais: Facts and figures about numbers and mathematics
660. Nombres 120 et 210 |
|
|||||||||
|
Deux nombres
"cousins" par leurs chiffres et par leurs propriétés avec les
nombres consécutifs. |
||||||||||
Nombre triangulaire et tétraédrique 120 = 1 + 2 + 3 + … + 15 = 1/2 (15 x 16) = 1
+ 3 + 6 + 10 + 15 + 21 + 28 + 36 Nombre triangulaire produit de
consécutifs 120 = 1 x 2 x 3 x 4 x 5
= 2 x 3 x 4 x 5
= 4 x 5 x
6 = 6! / 3! Nombre triangulaire, somme de
triangulaires 120 = T1 + T2 +…+ T8 = T15 |
Nombre triangulaire 210 = 1 + 2 + 3 + … + 20 = 1/2 (20 x 21) Nombre triangulaire produit de
consécutifs 210 = 5 x 6 x 7 = 7! / 4! Nombre triangulaire, somme de
triangulaires 210 = T4 + T5 +…+ T10 = T20 Nombre triangulaire, somme de
produits 210 = 1•2•3 + 2•3•4 + 3•4•5 + 4•5•6 Nombre triangulaire, divisions 210 = 7! / 4! = 9! / 123 |
|||||||||
|
Brèves associées |
>>>
Nombre 12
|
>>>
Brèves Nombres – Index |
||||||||
|
Pour en savoir plus |
>>>
Nombres triangulaires |
>>>
Nombres tétraédriques |
||||||||
661. Aire du rectangle dans carré |
|
|||||||||||||||||||||||||||
|
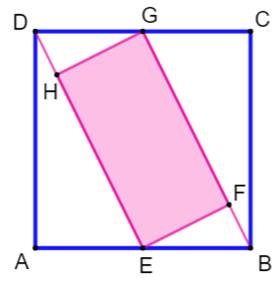
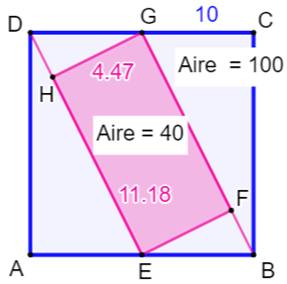
Énigme Un carré ABCD de côté 10. Les
milieux E et G. Un rectangle qui s'appuie sur
les semi-diagonales DE et BG. Quelle est l'aire du rectangle ? Solution Notez que, du fait des parallèles,
les triangles AED et BCG sont isométriques. Toujours avec les parallèles et
l'égalité des angles, les triangles ADE et HGD sont semblables. Le rapport
d'homothétie est k = DE / DG (rapport entre les hypoténuses). Calculs
|
|
|||||||||||||||||||||||||||
|
Brèves associées |
>>>
Rectangle
– Point interne |
>>>
Brèves Géométrie – Index |
||||||||||||||||||||||||||
|
Pour en savoir plus |
>>>
Rectangle |
>>>
Carrés – Index |
||||||||||||||||||||||||||
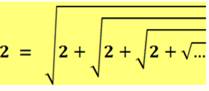
662. Nombre 2 et racines continues |
|
||
|
Une manière originale de démontrer que :
On part de la valeur du cosinus de Pi/4 et application de la formule
de l'angle
double. Ce procédé est répété pour des angles moitié à chaque fois. Calcul de la limite lorsque le dénominateur est infini; l'angle est
nul; et, cos 0 = 1 |
|
||
|
Brèves associées |
>>>
Nombre 2 |
>>>
Brèves Nombres – Index |
|
|
Pour en savoir plus |
>>>
Racines continues |
>>>
Nombre 2 en maths et culture générale |
|
663. Cercle interne au carré |
|
|||
|
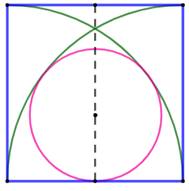
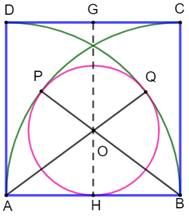
Problème Quel est de rayon du cercle interne au carré de
côté unité ? Le cercle est tangent au deux quarts de cercle et
à un côté du carré. Solution Soit la tangente en P au cercle rose et au cercle
vert. Sa perpendiculaire porte le centre de chaque cercle. Or, B est le
centre du quart de cercle. Le centre du cercle rose est donc sur le segment
PB. Même raisonnement pour le point Q. Le centre du
cercle rose se trouve sur AQ. Ce centre est donc à l'intersection O de AQ et
BP. Par symétrie le point O est aussi sur GH. Le triangle AOH est rectangle et: |
|
|||
|
Brèves associées |
>>>
Cercles
et triangles équilatéraux |
>>> Brèves
Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Cercle et sécante |
>>>
Sangakus |
||
664. Pentagone (très) approché |
|
|||
|
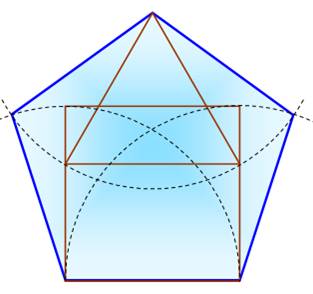
Construction simple
du pentagone qui s'approche du pentagone régulier à 4 pour 1000. Intérêt pour les arpenteurs: jardins, bassins,
bâtiments, etc. Il s'agit d'un triangle équilatéral emmanché dans
un carré en ses 2/3. Le sommet du triangle et les deux sommets à la base du
carré constituent trois sommets du pentagone. Construire les trois arcs de cercles figurés en
pointillés. Ils créent deux points d'intersections externes, les deux
derniers sommets du pentagone. |
Construction de Ian Mansour |
|||
|
Brèves associées |
>>>
Construction
du pentagone régulier >>>
Construction avec la fraction 10/17 |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Constructions approchées du pentagone |
>>>
Mesures dans le pentagone |
||
665. Nombres de Kimberling |
|
|||
|
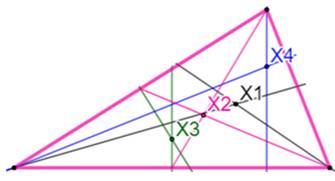
Kimberling
attribue un numéro aux points remarquables du triangle. Ainsi:
Vous
connaissez ces quatre points vus au lycée. Passionné, peut-être quelques
autres vous sont connus. Imaginez, en 2012, le répertoire de Kimberling en
compte plus de 42 000. |
Les quatre points classiques du
triangle et leur numéro de Kimberling
|
|||
|
Brèves associées |
>>>
Triangle
de Conway |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Nombres de Kimberling |
>>>
Éléments remarquables dans le triangle |
||
666. Équation en x45 |
|
||
|
En 1593, Adrianus Romanus
propose cette équation à ces contemporains. François
Viète (1540-1603), mathématicien français, est le premier à la résoudre.
Il a rapidement reconnu que l'équation était satisfaite par la corde d'un
cercle de rayon 1, sous-tendant un arc de 8° (2Pi/45). C'est la solution dont
disposait Romanus. En fait, Viète a
trouvé les 22 autres solutions
positives. Une amitié entre les deux mathématiciens se noue. À la fin du texte, Viète propose de résoudre le dernier
problème (le dixième) du traité perdu d'Apollonius: tracer un cercle
tangent à trois cercles donnés. |
Équation 45x – 3795x3 + 95634x5 + …+ x45 = N
Solution
|
||
|
Brèves associées |
>>>
Équation
de Bachet |
>>>
Brèves Équations – Index |
|
|
Pour en savoir plus |
>>>
Équation en x45 et Viète |
>>>
Équations |
|
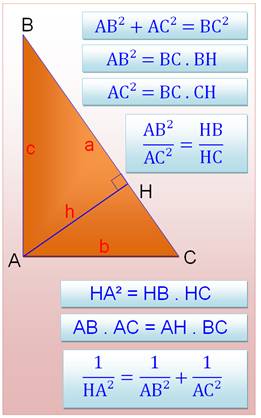
667. Triangle rectangle (suite) |
|
|||
|
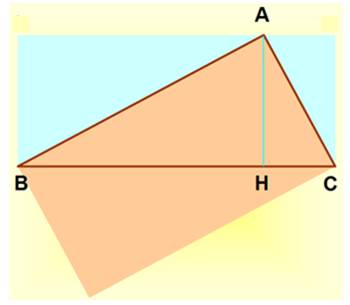
|
Une démonstration immédiate Égalité de l'aire des deux rectangles: AB · AC =
AH · BC
|
|||
|
Brèves associées |
>>>
Triangle
rectangle – Approche |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Triangle rectangle – Propriétés |
>>>
Triangle – Index |
||
668. Carré par quatre points |
|
|||
|
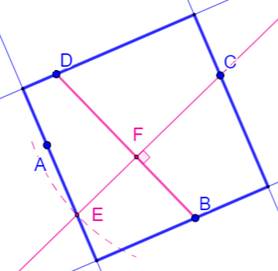
But Construire un carré passant par les points A, B,
C et D quelconques. Construction Segment DB. Segment CE perpendiculaire à
DB et avec CE = DB. Par B, C, D, E passent une infinité de carrés. Droite AE. Perpendiculaire en D à AE. Perpendiculaire en C à la
droite en D. Perpendiculaire en B à la
droite en C. Propriété utilisée Dans un carré deux sécantes perpendiculaires
découpent des segments de même longueur. |
|
|||
|
Brèves associées |
>>>
Polygones
rigides |
>>>
Brèves Constructions – Index |
||
|
Pour en savoir plus |
>>>
Rectangle et carré par quatre points |
>>>
Carré (géométrie) – Index |
||
669. Quatre nombres au carré |
|
|||
|
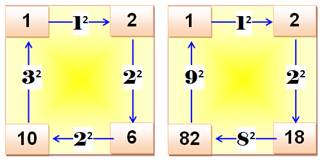
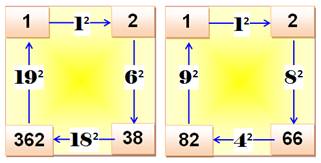
Quadruplet simple Trouvez trois nombres a, b,
c et d tels que: b – a = n² ; c –
b = m² ; d – c = p²; d – a = q² Les carrés se trouvent sur le périmètre. Quadruplet complet Le quadruplet est complet si
les deux différences sur les diagonales
sont aussi des carrés b – d = r²; c –
a = s² Ces quadruplets sont très rares! Imposer une somme carrée est un véritable
défi. Michel Rolle à trouvé un tel quadruplet dont les quatre nombres ont
sept chiffres. |
Exemples de quadruplets simples
|
|||
|
Brèves associées |
>>>
Carré et
cube à la fois |
>>>
Brèves Puissances – Index |
||
|
Pour en savoir plus |
>>>
Quatre nombres au carré |
>>>
Carré (nombres) – Index |
||
670. Énigme des âges |
|
|||
|
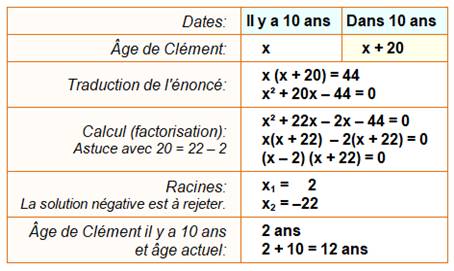
Problème Le produit de l'âge de Clément dans 10 ans par
celui qu'il avait il y a 10 ans est égal à 44. Quel est l'âge de Clément ? Commentaire Cas typique d'application de la résolution des équations
du deuxième degré par méthode de factorisation. Note Somme des racines: 2 – 22 = -20 Produit des racines: 2 x (-22) = -44 Valeurs présentes dans l'équation ! |
Solution par mise en équation
|
|||
|
Brèves associées |
>>>
La somme des deux âges |
>>>
Brèves Énigmes – Index |
||
|
Pour en savoir plus |
>>>
Énigmes sur les âges |
>>>
Âges devinés – Énigmes |
||
671. Dominos en carré |
|
||||
|
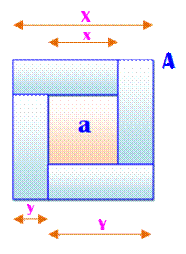
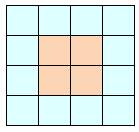
Énigme Un carré et quatre rectangles
(dominos) sont disposés pour former un grand carré (Voir illustration). On sait que l'aire du grand
carré (A) vaut quatre fois celle du carré interne (a) Quelle est le rapport entre la
longueur (Y) de chaque domino et leur largueur (y) ? |
|
||||
|
Solution la plus simple Calcul avec les aires:
|
Solution en image
|
||||
|
Brèves associées |
>>>
Énigme du parking |
>>>
Brèves Énigmes – Index |
|||
|
Pour en savoir plus |
>>>
Carrés – Propriétés |
>>>
Âges |
|||
672. Nombre 14 |
|
|||
|
Somme des
premiers carrés 14 = 1² + 2² + 3² = 1 + 4 + 9 Somme des
premières puissances de 2 14 = 21
+ 22 + 23 (= 1110 en binaire) Mêmes chiffres
de part et d'autre de l'égalité. 14 = 4 x 3 + 2 = 42
/ 3 |
Tous les
chiffres de 1 à 9, une seule fois avec ces deux puissances de 14.
|
|||
|
Brèves associées |
>>>
Nombre 13 |
>>>
Brèves Nombres – Index |
||
|
Pour en savoir plus |
>>>
DicoNombre 14 – Maths >>>
DicoNombre 14 – Culture |
>>> Motifs pannumériques |
||
673. Factorielle – Programme |
|
|||||
|
Rappel: exemple avec factorielle de 4 4! = 1 x 2 x 3 x 4 = 24 Programme conventionnel
|
Programme récursif
La fonction factorielle (fact) fait appel à elle-même pour calculer la
factorielle précédente (n – 1) jusqu'à descendre jusqu'à la factorielle 1
(cas avec n < 2). Alors le programme, ayant mémorisé toutes les valeurs, remonte la
chaine et calcule tous les produits. Ici 6! = 720 |
|||||
|
Brèves associées |
>>>
Mon tout
premier programme |
>>>
Brèves Programme – Index |
||||
|
Pour en savoir plus |
>>>
Programmation des factorielles >>>
Programmation Python |
>>> Programmes – Index >>>
Factorielle – Index |
||||
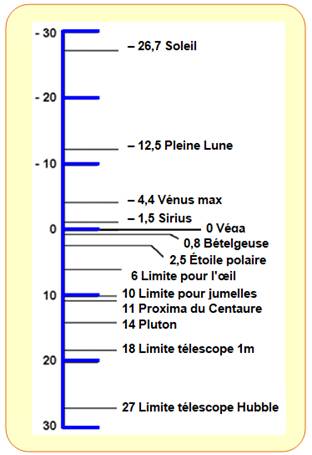
674. Magnitude des étoiles |
|
||||||
|
Soleil
Hubble
Référence
Magnitude 29
|
|
||||||
|
Brèves associées |
>>>
L'Univers
|
>>>
Brèves Astronomie – Index |
|||||
|
Pour en savoir plus |
>>>
Magnitude >>> Années-lumière |
>>>
Soleil >>> Télescope spatial Hubble |
|||||
675. Nombres triangles, carrés … |
|
|||
|
Théorème des nombres polygonaux
(Fermat -1636)
|
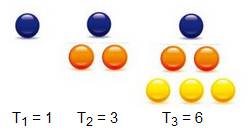
Nombres triangulaires
Nombres carrés
|
|||
|
Brèves associées |
>>>
Partitions
et nombres pentagonaux |
>>>
Brèves Théorie des Nbs – Index |
||
|
Pour en savoir plus |
>>>
Théorème des nombres polygonaux |
>>>
Nombres triangulaires >>>
Somme de quatre carrés |
||
676. Puissances en folie |
|
|||
|
Règles utilisées 1)
Le carré
d'un nombre négatif est positif. 2)
La racine
négative est en fait l'inverse de la racine positive. 3)
La racine
-1 est simplement l'inverse du nombre. |
Parenthèses internes (1)
Parenthèses du centre (2)
Parenthèses externes (3)
|
|||
|
Brèves associées |
>>>
Puissances
négatives de 2 |
>>>
Brèves Calculs – Index |
||
|
Pour en savoir plus |
>>>
Puissances et racines |
>>>
Puissances – Index |
||
677. Équation démystifiée |
|
|||
|
Il est fréquent de trouver des défis
mathématiques sur Internet, sur les forums ou sur les réseaux sociaux. Moins innocent, ceux proposés par des sites qui vous
attirent pour la publicité. L'équation de l'année en est un exemple. Résoudre
cette équation avec au dénominateur trois années qui se suivent.
|
Solution Avant de se lancer dans de longs calculs, on
observe cette équation qui comporte trois fractions et une somme qui vaut 3. Et si chaque fraction valait 1, nous tiendrions
notre solution. Et oui ! Avec x = 2021 (l'année suivante), chaque fraction
vaut 1. Pour la première, on a bien: 2021 – 3 = 2018. Ce motif est valable pour toutes les années et,
on peut même augmenter le nombre de termes. |
|||
|
Brèves associées |
>>>
Équations et Racines – Un bon truc! |
>>>
Brèves Équations – Index |
||
|
Pour en savoir plus |
>>>
Équations pour débuter >>>
Énigmes virales du Net |
>>>
Années 2021 avec humour >>>
DicoNombre 2021 |
||
678. Aire mystère du rectangle |
|
|||
|
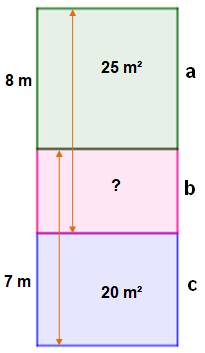
Aire du rectangle rose ?
|
Solution logique S'agissant d'une énigme, sans doute faut-il
réfléchir avant de lancer un calcul d'équations. La solution est sans doute
en nombres entiers. L'aire du rectangle central serait alors un
multiple de 5 comme les deux autres. Si c'est le cas:
C'est compatible ! Et c'est donc la bonne
solution. Aire du rectangle rose central: 5 x 3 = 15 m². Solution algébrique (Désolé ! Inversion de a et c sur
ce tableau)
|
|||
|
Brèves associées |
>>>
Aire des parallélogrammes |
>>>
Brèves Énigmes – Index |
||
|
Pour en savoir plus |
>>>
Rectangle |
>>>
Énigmes – Index |
||
679. Phi et 1/Phi en puissance |
|
|||
|
Le nombre d'or et son inverse
|
Différence et somme en puissances
|
|||
|
Table des valeurs entières pour k
de 1 à 10
|
||||
|
Brèves associées |
>>>
Phi = 1,618… - d'or |
>>>
Brèves Nombres – Index |
||
|
Pour en savoir plus |
>>>
Nombre d'or et puissances |
>>>
Nombres entiers |
||
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()