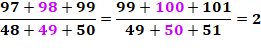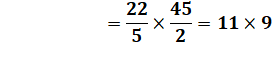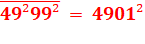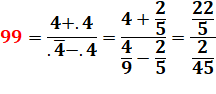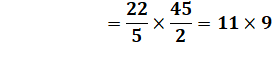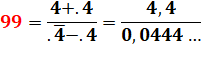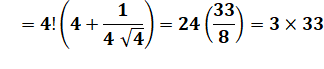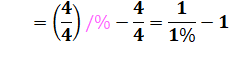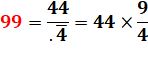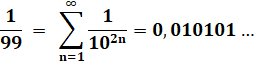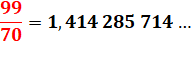|
||||||||||||||||||||||||||||||||||||||||||
![]()
|
C'est ainsi, je vous le dis, qu'il y aura plus de joie dans le ciel
pour un seul pécheur qui se repent que
pour quatre-vingt-dix-neuf justes, qui
n'ont pas besoin de repentir. |
|
|
Le génie représente 1% d'inspir 99% de transpiration. Thom |
Pour être grand, il
faut quatre-vingt-dix-neuf pour cent de
travail. Willi |
Voir
Pensées & humour
|
|
||||||
|
|
Voir Numération 90 à 99 |
|||||

|
|
||
|
|
||
|
Mais "quelques" c'est bien moins que 99 ! |
||
|
|
||
|
|
||
|
Quelques extraits: Neun und neunzig
Luftballons (99 ballons) Auf ihrem Weg zum horizont (En route
vers ton horizon) … Neun und neunzig
Düsenflieger (99 pilotes d'avions à réaction) Jeder war ein grosser Krieger
(Chacun d'entre eux était un grand guerrier) … Neun und neunzig
jahre Krieg (99 années de guerre) Liessen keinen platz für Sieger
(N'avaient même pas laissé de place pour les vainqueurs) … |
||
|
|
||
|
|
||
|
J'entre
dans un magasin avec 99,98 euros. J'en dépense la moitié. Il me reste autant
de centimes que j'avais de francs et la moitié des francs que j'avais de
centimes. |
||
|
Amusement
qui consiste à lire le nombre quatre-vingt-dix-neuf (4, 20, 10, 9) et à
ajouter les nombres lus (43), auquel n ajoute 1. |
||
|
|
||
|
|
||
|
|
||
|
L'atome
est extrêmement vide! |
||
|
|
||
|
Pourquoi les prix se terminent par 9 ? Un
jour, quelque part, un commerçant constate qu'avec des prix ronds, les
employés "oubliaient" de les encaisser et gardaient cet argent pour
eux. D'où l'idée de mettre des prix qui imposaient de passer par la caisse
pour rendre la monnaie. L'attrait
marketing d'un prix inférieur à 1 euro (ou autre devise) n'a été constaté
qu'après coup. Schindler et Kibarian – 1996: Results showed that the use of 99 endings led to increased consumer
purchasing. This demonstrates the importance of the manager's decision
concerning a price's rightmost digits.
Les résultats ont montré que l'utilisation de 99
terminal entraînait une augmentation des achats des consommateurs. Cela
démontre l'importance de la décision du gestionnaire concernant les chiffres
les plus à droite d'un prix. |
|
|
||
|
Nombres
en 9 101 – 1 = 9 102 – 1 = 99 103 – 1 = 999 … Base de l'explication de la preuve
par 9. |
Voir Nom des nombres Voir Nombres
géométriques |
|
Numération / Chiffres
|
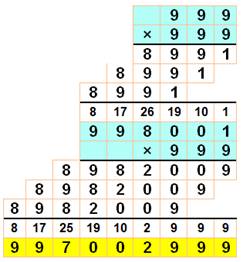
99 – 9 – 9 = 81 = 34
= 9² |
||
|
99 = (9x9) + (9+9) 99² = 9 801 99 = (9x9) + (9+8+0+1) = 81 + 18 |
Nombre
égal à produit des chiffres + somme des chiffres, comme tous les nombres à
deux chiffres terminés par 9. Égalité
aussi avec les chiffres du carré (99² = 9 801). |
|
|
99 = 9+5+0+9+9+0+0+4+9+9 +
9+4+1+4+8+0+1+4+9+4+0+1 |
Somme
avec ses chiffres et ceux de ses puissances. |
|
|
Pour la suite, dans le DicoNombre, on ne
présentera que quelques nombres narcissiques de Keith particuliers. Pour
plus de ces nombres voir la Table des
nombres de Keith |
||
|
99
9 + 9 = 18 & 9 x 9 = 81 |
|
|
99 = (9 x 9) + (9 + 9)
= 81 + 18 |
Vrai
pour tous les nombres à deux chiffres terminés par 9. |
|
99 = 9 + 9x9 + 9 89 = 8 + 8x9 + 9 |
|
|
99 = (22+2) + (22-2) + (22x2) + (22/2) |
|
Addition-Soustraction
|
99 = 4 + 5 +
… + 13 + 14 99 = 7 + 8 +
… + 14 + 15 99 = 14 + 15
+ … + 18 + 19 99 = 32 + 33
+ 34 99 = 49 + 50 |
|
|
99 = 7 + 8 +
… + 15 = (16 + 17) x 3 |
|
|
99 = 1 + 3 + 4 + ...
+ 12 |
|
|
99 = 90 + 09 = 18
+ 81 = 27 + 72 = 36 + 63 = 45 + 54 |
|
|
100, 101,
110, 112, 121, 122, 211, 212, 221,
223, 232, 233, 322, 323, 332, 334, 343, 344, 433, 434, 443, 445, 454, 455,
544, 545, 554, 556, 565, 566, 655, 656, 665, 667, 676, 677, 766, 767, 776,
778, 787, 788, 877, 878, 887, 889, 898, 899, 988, 989, 998. |
Exemple: 112 => 211 – 112
= 99 |
Multiplication
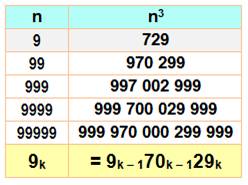
Multiplication
transformée en soustraction
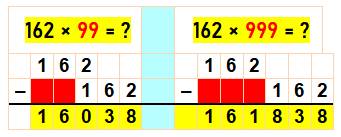
Décalage
de k crans car présence de k fois le 9.
|
|
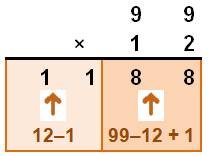
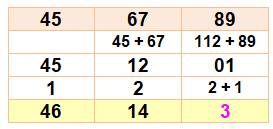
1) le
nombre moins 1 pour les centaines, et 2) la
soustraction du nombre à 99 plus 1 pour les unités. Voir Brève 55-1086 |
|
99 = 9 x 11
= 100 – 1 |
Division
|
|
|
||
|
102 – 1 = 99 104 – 1 = 99 x 101 |
|
||
|
…
87, 93, 99, 105 … |
|
||
|
Div(99) = {1, 3,
9, 11, 33, 99} 99 = 49 + 50(2) = 32 + 33 + 34(3) = 14 + 15 + 16 + 17 + 18 + 19(6) =
7 + …+ 11 + … + 15(9) =
4 + … + 9 + … + 14(11) |
|
||
|
|
|
||
|
456789 = 99
x 4614 + 3 |
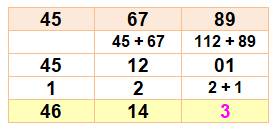
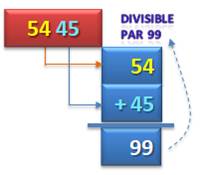
Partager
le nombre en blocs de 2 chiffres à partir de la droite. Ajouter
le bloc suivant à la somme complète obtenue. Les retenues sont abaissées Le
reste est réalisé avec la somme finale: (dizaine-unité + centaine). Ici: 01 +
2 = 3. |
||
|
|
Constituer
des blocs de 2 chiffres et les additionner. |
||
|
1 287 = 99
x 13 avec 1 + 8 = 9 et 2 + 7 = 9 et 13 = 12 + 1 |
|
||
|
99 |
10 99+1 – 1 |
|
||
|
99
|
|
|
|
99 = 1² + 7² + 7² = 3² + 3² + 9² = 5² + 5² + 7² |
|
|
|
99 = 1² + 1² + 4² +
9² = 1² + 3² + 5² + 8²
= 3² + 4² + 5² + 7² |
|
|
|
99 = 91 +
91 + 92 |
||
|
99 = 50² – 49² = 50 +
49
= 18² – 15²
= 10² – 1² |
|
|
|
99 = 23 +
33 + 43 = 9 x 11 = 8 + 27 + 64 |
|
|
|
99 = 23 +
33 + 43 = 9 x 11 |
Voir Autour de 1 2 3 4 5 |
|
|
99 = 23 +
33 + 43 =
8 + 27 + 64
= 53 + 13 – 33 = 125 + 1
– 27
= 23 – 53 + 63 = 8 – 125
+ 216
= 163 + 363 – 373
=
4096 + 46 656 – 50 653 |
|
|
Petit
calcul
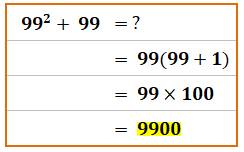
|
|
|
|||
|
|
|
|||
|
99 = 2 × 7² +
1 99² =
2 × 70² + 1 |
|
|||
|
299 ≡ 17 mod 99 |
|
|||
|
99² = 9801 et 98 + 01 = 99 33² = 1089 et 10 + 89 = 99 66² = 4356 et 43
+ 56 = 99 |
Tous les repdigits en 9 sont Kaprekar d'ordre 2. Voir Brève
634 |
|||
|
99 = 98 +
01 999²
= 998 001 999
= 998 + 001 993 =
97 02 99 99
x 2 = 97 + 02 + 99 994 = 96 05 96 01 99
x 2 = 96 + 05 + 96 + 01 |
Voir Calcul du
carré des nombres en
99 …9 |
|||
|
|
|
|||
|
99² = 2 x 70² + 1 9 801 = 2 x 4 900 + 1 |
|
|||
|
99² = 101² – 20²
La dernière égalité 1234567898765432099² + 2222222220² =
1234567898765432101² =
1524157896662094204572473697241274201 = 1,52… 1036 |
Un des
nombreux motifs de cette sorte créés par Inder J. Taneja |
|||
|
99² – 1 = 9 801 – 1 = 23 ٠ 52 ٠ 72 |
|
|||
Infinité de triplets de Pythagore

Voir Nombre 21 / Autres
formes de ce type
|
993 = 970 299 = 98 ×
99 ×
100 + 99 =
(100 – 2)(100 – 1) × 100 + 99 = 1 000 000
– 30000 + 200
+ 99 = 970 299 |
|
||
|
993 = 970299
|
|
||
|
729
= 51998697814228992
=> 5+1+9+…+2 = 99 9910
= 90438207500880449001
=> 9+0+4+…+1 = 72 |
|
||
|
|
Voir Démonstration
de 50^99 > 99! |
||
Dénombrement, jeux et curiosités
|
|
|
|
|
|
99 |
|
|
|
|
|
|
||
|
= 24019801 or 2401 =49² et
9801 = 99² |
|
||
|
3 x 9 = 27 3 x 99 = 297 3 x 999 = 2997 … |
|
||
|
321 – 123 = 198 =
99 x 2 99 x 5 = 495 &
495 + 594 = 1089 99² =
9801 |
|
||
Jeu du
quatre"4"
|
|
Avec
la notation .4 = 0,4 = 2/5 et .4
surligné = 0,444… = 4/9 |
|
|
Solution
1: avec .4 = 0,4 = 2/5 et .4 surligné =
0,444… = 4/9 Solution
2: déroge à la règle avec l'introduction d'un "1". |
|
|
|
|
99! = 9,332...99...9999...99... 10155 = 37,6231004…99 |
|
|
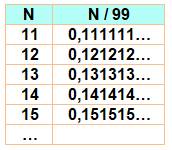
1 / 99 = 0,01010101... abc… / 999 …= 0,abc abc … Ex: 456/999 = 0,456 456 … |
|
|
|
|
|
99 = 44/ .44… |
|
|
|
à
72 10 -6 près. |
|
99 |
10 99+1 – 1 |
|
|
x + x2
+ x3 = 99 + 992 + 993 |
|
|
|
Voir Diviseurs, Quantité,
Somme,
Fonctions
arithmétiques
|
Numération: base, [chiffres] |
Repdigit (Brésilien) |
||
|
2, [1, 1, 0, 0, 0, 1, 1] 3,
[1, 0, 2, 0, 0] 4, [1, 2, 0, 3] 5,
[3, 4, 4] 6, [2, 4, 3] 7,
[2, 0, 1] 8,
[1, 4, 3] 9,
[1, 2, 0] 10, [9, 9] 11,
[9, 0] |
12,
[8, 3] 13,
[7, 8] 14,
[7, 1] 15,
[6, 9] 16,
[6, 3] 17,
[5, 14] 18,
[5, 9] 19,
[5, 4] 20,
[4, 19] 21,
[4, 15] |
22,
[4, 11] 23,
[4, 7] 24,
[4, 3] 25,
[3, 24] 26,
[3, 21] 27,
[3, 18] 28,
[3, 15] 29,
[3, 12] 30,
[3, 9] 60,
[1, 39] |
10,
[9, 9] 32,
[3, 3] 98,
[1, 1] |
Voir Bases
/ Brésiliens
![]()
|
Suite |
|
|
Cette page |
![]()