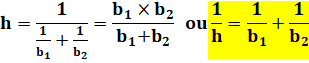|
||||||||||||||||||||||||||||
![]()
|
Le puits et les deux barres au fond Calculs de géométrie simple
ou plus compliqué avec deux barres appuyées au fond d'un puits en forme de U. La hauteur du point de croisement
ne dépend pas de la taille du fond du puits. |
|
|
||
|
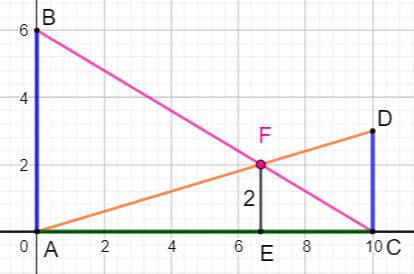
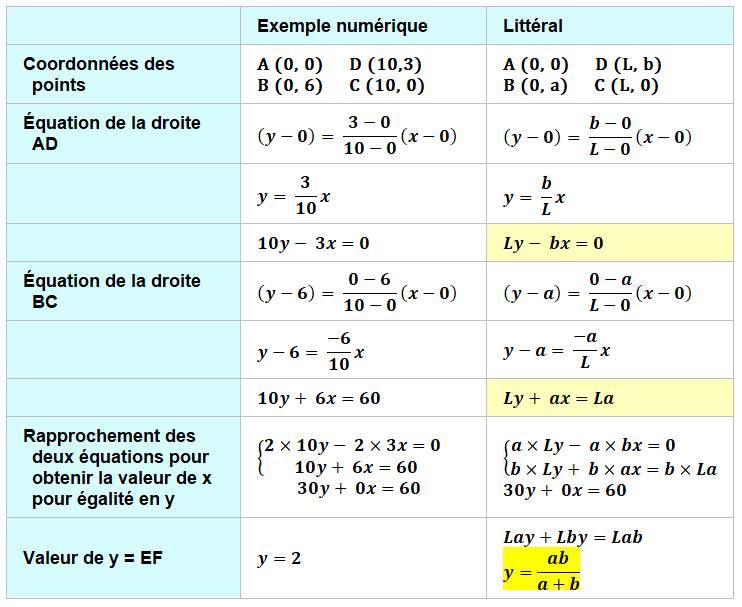
Construction La base AC est de longueur L variable. Deux barres verticales AB et CD de longueur a et
b. Deux barres obliques AD et BC. Propriété La hauteur EF du point d'intersection F ne dépend
que de AB et CD, mais pas du tout de L = AC |
|
|
|
Calcul analytique (avec équation
de la droite)
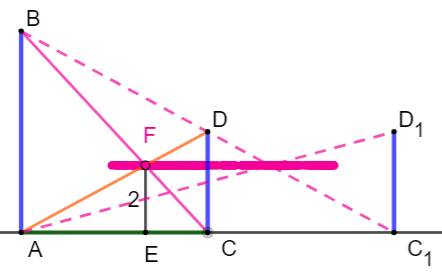
Trace du point F en déplaçant C sur la droite AC
|
||
Voir Brève
864
|
|
||
|
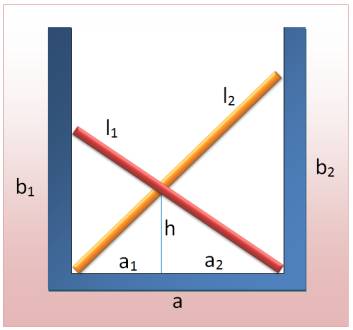
Deux barres se croisent au
fond d'un puits. Quelle est la hauteur
h du point de croisement? On connaît la longueur des
barres (l1 et l2), de même que la largueur du puits
(a). Pythagore
Thalès
En additionnant:
Et pour h
|
Exemple: a = 3 m ; l1
= 4,25 m et l2 = 6,7 m b1 = 3 m et
b2 = 6 m h = 2 m (précisément: 2,00359123 …) |
|
Voir
Théorèmes de Thalès et de Pythagore
Cas où
toutes les longueurs sont des entiers
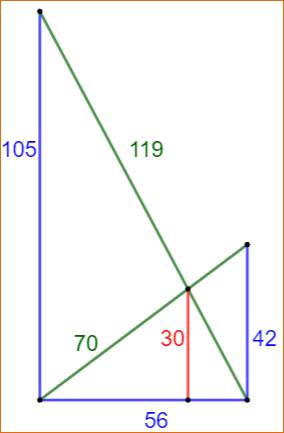
Cas rare !
|
|
|
|
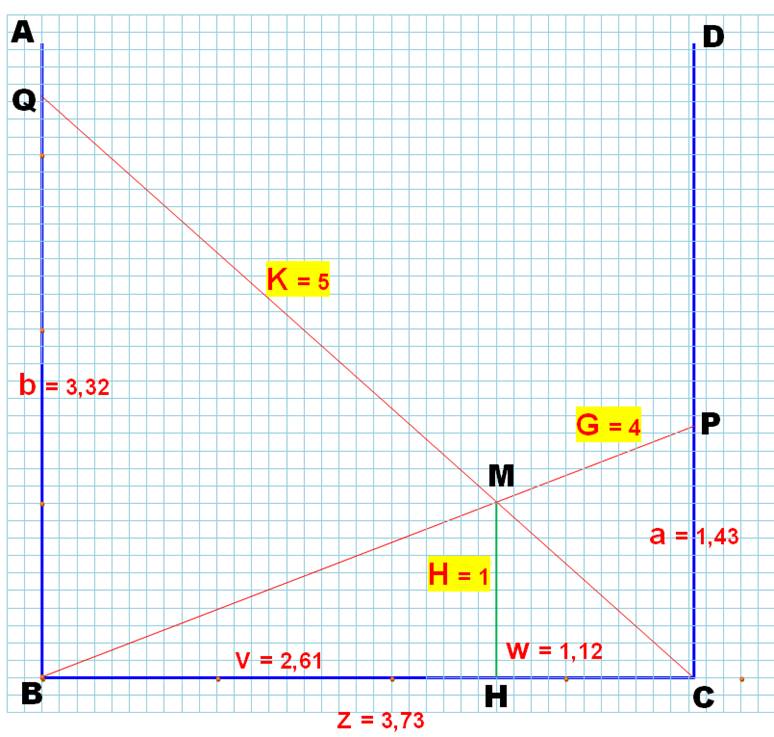
Problème Une cuve en forme de U: ABCD Deux obliques: BP et CQ,
mesurant respectivement 4 et 5 m. La hauteur du point de leur
intersection HM = 1 m. Quelle est la taille du fond de cuve: z = BC ? Solution sur cette illustration Z = 3, 735508533 …
|
|
|
|
|
|
Résolution avec Thalès et Pythagore
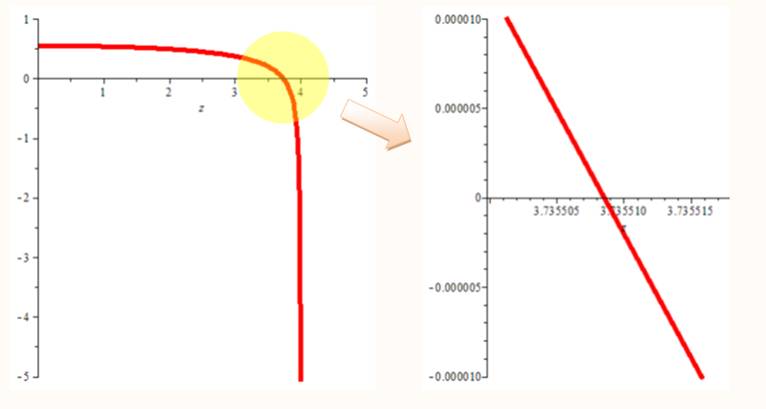
Cette équation n'est pas simple à résoudre
analytiquement. Voici sa forme:
Graphe de cette fonction pour détermination
graphique de la racine
Solution analytique
Formule dépliée pour z
= 3,735 508 533 413 253 045 4… |
|
Bilan
|
La solution de ce
deuxième problème exige l'utilisation d'outils mathématiques. Existe-t-il une
solution plus simple, plus astucieuse? |
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()