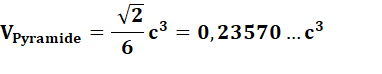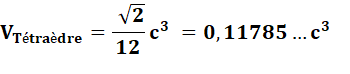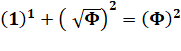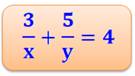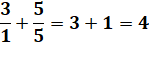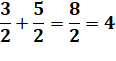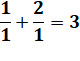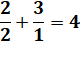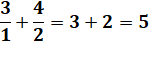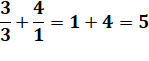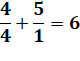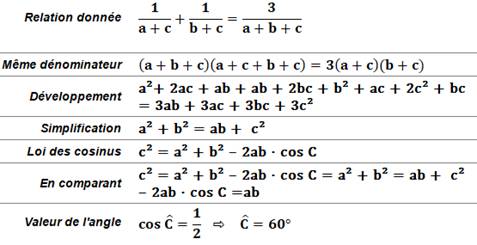NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 03/10/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 10		Page 20		Page 30		Page 40			Page 50
	Page 30 (480-599)		Page 31 (600-619)		Page 32 (620-639)		Page 33 (640-659)		Page 34 (660-679)
	Page 35 (680-699)		Page 36 (700-719)		Page 37 (720-739)		Page 38 (740-759)		Page 39 (760-779)

BRÈVES de MATHS – Page 35

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

680. Pyramide et tétraèdre
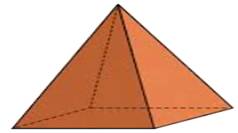
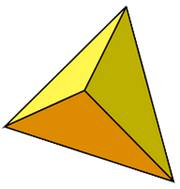
On compare le tétraèdre et la pyramide à base carrée pour lesquels les triangles équilatéraux des faces sont identiques. Soit c la longueur des 14 côtes. À faces égales, le volume de la pyramide est le double de celui du tétraèdre.
Brèves associées	>>> Sphère et cylindre – Archimède	>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Pyramide à base carrée	>>> Tétraèdre

681. Trois cercles dans un rectangle
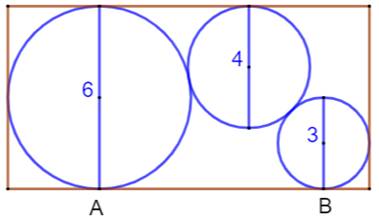
Problème Trois cercles dont le central tangent aux deux autres, et tous les trois sont tangents au rectangle. Quelle est la longueur du segment AB ?
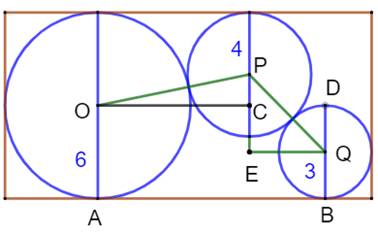
Solution Avec le théorème de Pythagore: La somme:
Brèves associées	>>> Cercles dans le carré		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Trois cercles tangents		>>> Sangakus

682. Cinq quadrilatères – Van Aubel
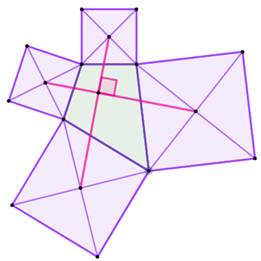
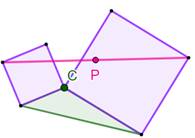
Construction Un quadrilatère quelconque (vert). Un carré apposé sur chaque côté vers l'extérieur. Leurs diagonales et leur centre. Propriétés: théorème de Van Aubel (1878) Les deux segments joignant les centres opposés ont même longueur et ils sont perpendiculaires. Si deux côtés sont alignés, le quadrilatère devient triangle et la propriété est conservée. Si la quadrilatère est un parallélogramme, les quatre centres forment un carré. Théorème de Thébault (1937)
Brèves associées	>>> Quadrilatère – Centre de gravité		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Théorème de Napoléon		>>> Carrés >>> Quadrilatères

683. Théorème de Bottema
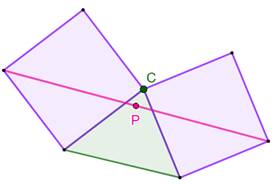
Construction Un triangle quelconque (vert). Un carré apposé sur deux côtés vers l'extérieur. Le segment joignant deux sommets opposés Propriétés: théorème de Bottema (1901-1992) Le point milieu P est fixe quelle que soit la position du point C.
Brèves associées	>>> Triangle de Conway		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Triangles – Index >>> Figure de Vecten		>>> Carrés

684. GAFAM et TRILLION de dollars

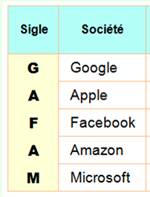
Grands nombres

1 trillion américain = 1 billion français

= 1 000 milliards = 10¹²

Les cinq grandes sociétés du numérique

Chiffre d'affaires le 28 juin 2021

en trillons de dollars

(mille milliards de dollars)

pour les six sociétés en tête

Apple	2,249
Microsoft	2,024
Saudi Arabian Oil Co	1,87
Amazon	1,74
Alphabet (Google)	1,67
Facebook	1,008
Total	10,561
Total GAFAM	8,691

Brèves associées

>>> Quantité de sable dans l'Univers

>>> Brèves Économie – Index

Pour en savoir plus

>>> GAFAM

>>> Trillion

>>> Noms des grands nombres

685. Cornet de glace
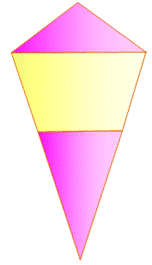
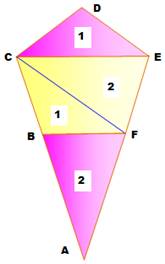
Énigme Un cornet de glace avec fraise, vanille et fraise. La section plane montre un triangle isocèle surmonté d'un pentagone régulier. Quelle est la plus grande surface: la rose ou la jaune ? Solution Les triangles roses (1 et 2) se retrouvent dans la partie jaune. L'aire rose est égale à l'aire jaune. Explications Les côtés des triangles CDE et FBC sont égaux deux à deux. Les deux triangles sont égaux (superposables). Les angles BAF et ECF valent 36°. BF = FE = côté du pentagone. Les triangles isocèles ABF et CFE, avec un côté égal et l'angle au sommet égal, sont égaux.
Brèves associées	>>> Triangle isocèle		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Énigmes avec le pentagone		>>> Énigmes et jeux – Index

686. Triangles dans pentagone
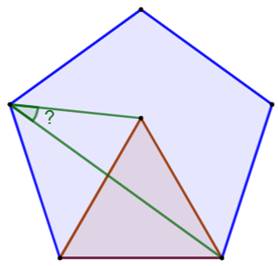
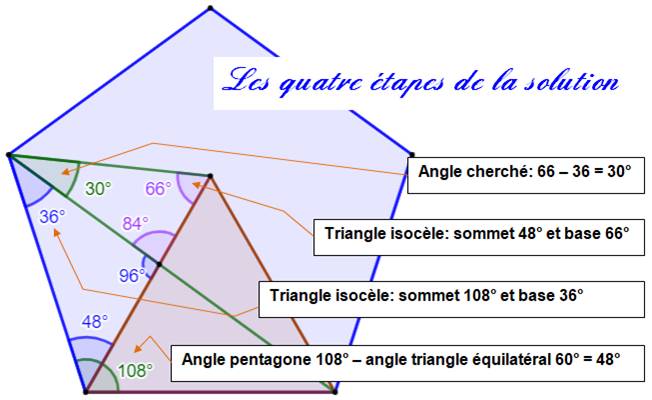
Énigme Un pentagone régulier. Un triangle équilatéral posé sur un côté du pentagone. Quelle est la valeur de l'angle formé par des deux segments figurés en vert ? Solution Le pentagone et le triangle ont des côtés de même longueur d'où la création de triangles isocèles. Dans un triangle isocèle, l'angle à la base vaut la moitié de 180° diminué de l'angle au sommet.
Lire du bas vers le haut
Brèves associées	>>> Cercles dans le carré	>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Énigmes avec le pentagone >>> Angles dans le pentagone	>>> Angles

687. Deux cercles tangents
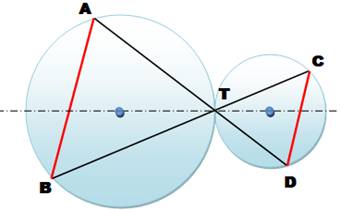
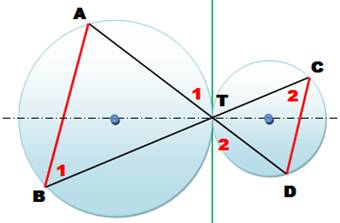
Problème Deux cercles tangents en T. Deux sécantes passant par T et coupant les cercles en A, B, C et D. Montrer que les droites passant par AB et CD sont parallèles. Solution (figure du bas) On trace la tangente commune en A (verte) et la solution devient évidente. Application du théorème des angles alternés dans chacun des cercles (interception du même arc): les angles marqués 1 sont égaux (arc AT); les angles marqués 2 sont égaux (arc TD). Or, les angles 1 et 2 en T sont égaux. L'angle en B est égal à l'angle en C. Même chose pour l'angle en A qui est égal à l'angle en D. Les deux triangles sont semblables et les troisièmes côtés, AB et CD, sont parallèles.
Brèves associées	>>> Cercles et triangles équilatéraux		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Théorème des angles alternés		>>> Cercles – Index

688. Nombre 15
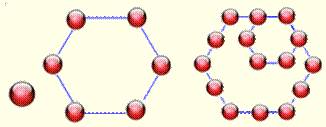
Somme des premières puissances de 2: 15 = 2^3 + 2^2 + 2^1 + 2^0 (1111 en binaire) Combinaisons de 6 objets pris 2 par 2 ou 4 par 4. Valeur qui se lit dans le triangle de Pascal. 15 = C6^2 = C6^4 Somme de nombres consécutifs de 1 à 8: 15 = 1 + 2 + 3 + 4 + 5 = 4 + 5 + 6 = 7 + 8		Troisième nombre hexagonal Préfixes diviseurs et multiplicateurs: 10^-15 femto 10^15 péta
Brèves associées	>>> Nombre 14		>>> Brèves Nombres – Index
Pour en savoir plus	>>> DicoNombre 15 – Maths >>> DicoNombre 15 – Culture		>>> Triangle de Pascal >>> Préfixes pour grands nombres

689. Nombre 153 et cubes
Stupéfiante somme de cubes: les nombres se retrouvent dans la somme & Calcul des deux premières sommes qui montrent que cet effet n'est pas si évident. Ce type de nombres est dit narcissique et ils ne sont pas nombreux.
Suite d'égalités sans fin			Calculs
Brèves associées	>>> Nombre 15	>>> Brèves Nombres – Index
Pour en savoir plus	>>> DicoNombre 153 >>> Démonstration de cette suite	>>> Nombres narcissiques >>> Pépites numériques

690. Aire mystère du triangle
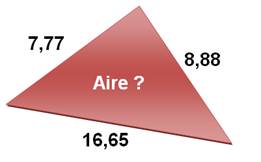
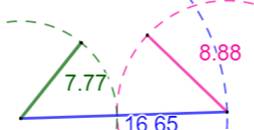
Énigme Inégalité triangulaire Dans un triangle, la somme des longueurs de deux côtés est toujours supérieure à la longueur du troisième côté.		Solution Le calcul semble inabordable. Comment s'y prendre ? J'entreprends d'en faire le dessin à l'échelle. Eh oui, la somme des longueurs des deux côtés est égale à celle du troisième côté. Il n'a pas de triangle; L'aire est nulle. Note: dans le cas général, la résolution d'un tel problème dit LLL, il faut faire appel à la trigonométrie.
Brèves associées	>>> Aire mystère du rectangle		>>> Brèves Énigmes – Index
Pour en savoir plus	>>> Inégalité triangulaire >>> Résolution du triangle LLL		>>> Énigmes – Index

691. Triangle de Kepler
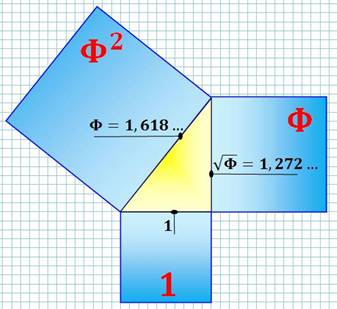
Triangle rectangle dont les longueurs des côtés sont en progression géométrique de raison dorée. Basé sur la relation du nombre d'or qui épouse le théorème de Pythagore:
Brèves associées	>>> Triangle de Conway		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Nombre d'or >>> Triangle rectangle		>>> Progression géométrique >>> Triangles – Index

692. Factorielles et files indiennes
La maitresse demande aux élèves de se placer à la file indienne. Combien de dispositions possibles avec 2, 3, …, k élèves ? Réponse avec la diapositive créée par Nathan 8 ans.
Brèves associées	>>> Factorielles	>>> Brèves Compter – Index
Pour en savoir plus	>>> Factorielles – Introduction et Index	>>> Dénombrement – Index

693. Théorème de la carpette
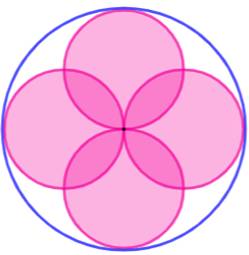
Tapis circulaires Le sol a la forme d'un grand cercle de rayon R. on y place quatre petits tapis en forme de cercle de rayon r = R/2. En théorie, ces quatre tapis pourraient donc couvrir exactement la surface du sol. Condition qui permet d'appliquer le théorème de la carpette. Théorème de la carpette (ou du tapis) – Carpet theorem Disposés avec recouvrement, la partie de chevauchement (rose foncé) occupe exactement la même surface que les quatre zones blanches non couvertes en périphérie.			Aire des zones blanches périphériques = aire de la rosace en rose foncé.
Brèves associées	>>> Sangakus	>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Théorème de la carpette	>>> Pavages

694. Triangle dans rectangle
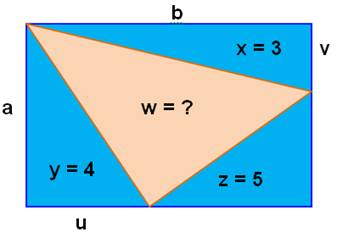
Énigme Un rectangle avec un triangle inscrit. Avec les aires données, calculer l'aire w. Solution Tactique de calcul Calculer les dimensions u et v avec les aires x et y, puis injecter ces valeurs dans le calcul de z.
Brèves associées	>>> Rectangle dans carré – Aire		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Quizz de géométrie (20 problèmes)		>>> Rectangle

695. Triangles dans le carré
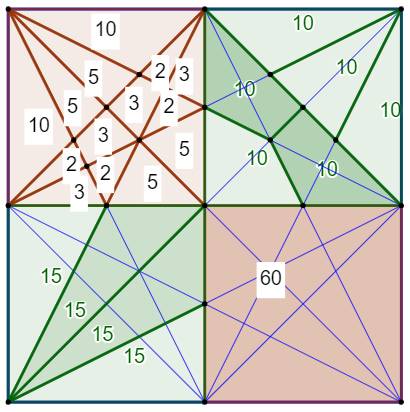
Construction Un carré, ses points milieux. Les seize segments joignant les huit (plus un) points du carré. Propriétés Tous les triangles élémentaires, formés par ces droites, ont des aires proportionnelles. À partir d'un carré de 240 cm², soit 60 cm² pour un quadrant, on y trouve des triangles avec des aires de : 2, 3, 5 et 10 cm². Pour information Côté du carré: Diagonale du carré:
Brèves associées	>>> Triangle – Partage en six parts égales		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Carré		>>> Compter les segments

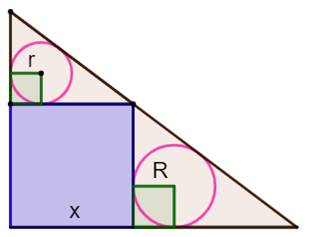
696. Sangaku à deux cercles
Construction Un triangle rectangle, son carré inscrit sur les côtés de l'angle droit et des deux cercles inscrits dans les deux triangles résultants. Propriété Démonstration Calcul de l'aire du triangle supérieur de deux façons en fonction de r et injection de R par relation de similitude.
Brèves associées	>>> Sangaku à deux cercles tangents		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Démonstration de ce Sangaku		>>> Sangakus

697. Fractions – Nombres consécutifs
Solutions de (3, 5, 4): Deux seules solutions:		Avec (1, 2, 3) : 1 solution Avec (2, 3, 4) : 1 solution		Avec (3, 4, 5) : 2 solutions Avec (4, 5, 6) : 1 solution
Brèves associées	>>> Fractions avec des briques type Lego		>>> Brèves Opérations – Index
Pour en savoir plus	>>> Fractions unitaires		>>> Calcul – Fractions – Index

698. Rectangle inscrit
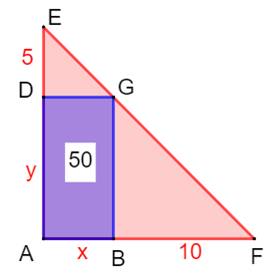
Énigme Un triangle rectangle et un rectangle inscrit dans son angle droit, éloigné de 10 et 5 par rapport aux deux autres sommets du triangle. Propriétés L'aire du rectangle est toujours égale au produit 10 x 5 = 50. L'aire minimale du triangle est obtenue pour x = 10 et y = 5, les valeurs d'éloignement.
Brèves associées	>>> Rectangle divisé en neuf, périmètre		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Théorème de Thalès et ses applications		>>> Théorème de Thalès

699. Loi des cosinus
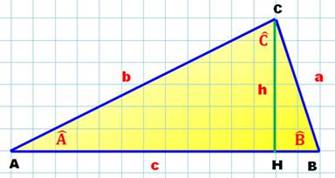
Loi des cosinus Dans tout triangle: Application Quel est l'angle C du triangle tel que:		Triangle quelconque Calculs
Brèves associées	>>> Triangle – Périmètre minimum		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Loi des cosinus		>>> Triangle quelconque ou scalène ?

Retour	Brèves de maths – Page 34
Suite	Brèves de maths – Page 36
Voir	Voir liens en haut de page Quizz de géométrie (20 problèmes)
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve35.htm