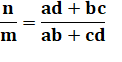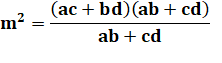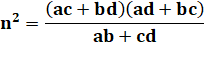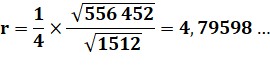Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 09/02/2024 M'écrire Brèves de Maths

INDEX Polygones Carrés Géométrie Dénombrement Défi en géométrie Jeux et énigmes	QUADRILATÈRES – Compter
	Quadrilatère	Triangles dans rectangle	Grille & segments
		Angles dans la quadrilatère	Quadrilatère inscriptible
	Carré	Triangle dans le carré	Grille & triangles rectangles
	Rectangle	Carrés et cercles	Grille & triangles équilatéraux
	Trapèze	Carré (un) dans le carré	Grille & carrés
		CARRÉS dans le carré
	Parallélogramme	Carrés dans rectangle	Rectangle en 3 triangles
	Losange	Rectangles dans carré	Rectangles – Énigmes
	Polygones	Rectangle dans rectangle	Pièce de puzzle
		Quadrilatère dans le carré

Faites un double-clic pour un retour en haut de page

QUADRILATÈRE Inscriptible ou Cyclique Propriétés – Énigme Propriétés du quadrilatère quelconque: aire, diagonale, … Quel est le rayon du cercle circonscrit ? Propriétés amusantes …
	Sommaire de cette page >>> Approche >>> Théorème de Pitot >>> Droites dans le quadrilatère cyclique >>> Aire du quadrilatère cyclique >>> Rayon du cercle circonscrit >>> Médiane-hauteur >>> Cercles internes	Débutants Géométrie Glossaire Géométrie

Approche		haut
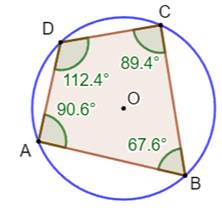
Définition Un quadrilatère inscriptible ou cyclique est un polygone à quatre côtés inscrit dans un cercle. Cela signifie qu’il existe un cercle qui passe par les quatre sommets du quadrilatère. Les sommets sont dits cocycliques. Le centre du cercle est appelé centre circonscrit et le rayon du cercle est appelé rayon circonscrit. Angles La somme des angles internes (en vert) vaut 360°. Les angles internes opposés sont supplémentaires (somme 180°). 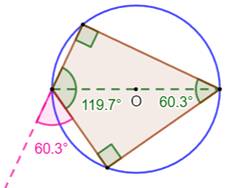L'angle externe d'un sommet est égal à l'angle interne du sommet opposé (exemple 60,3°, en bas). Dans le cas où, deux sommets opposés sont les extrémités d'un diamètre, deux de ses angles sont droits (figure du bas). Les diagonales sont orthogonales. Aire maximale Le quadrilatère d'aire maximale, les longueurs des côtés étant fixées, est le quadrilatère inscriptible.	Quadrilatère inscriptible Deux sommets sur un diamètre Quadrilatère inscriptible orthodiagonaux

Théorème de Pitot (1695-1771)		haut
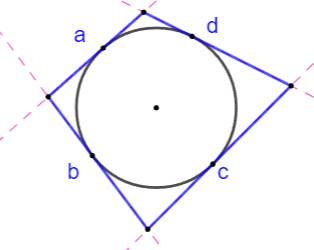
Théorème de Pitot Si un quadrilatère est circonscriptible (c'est-à-dire si ses quatre côtés sont tangents à un même cercle), alors la somme des longueurs de deux côtés opposés est égale à la somme des deux autres. a + c = b + d Cette égalité découle immédiatement de la propriété des tangentes: les segments de tangentes issues d'un point sont isométriques.

Droites dans le quadrilatère cyclique		haut
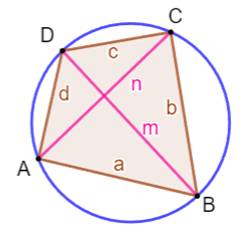
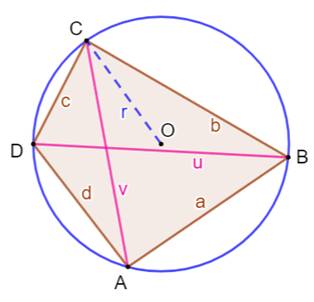
Propriétés des diagonales Théorème de Ptolémée (vers 100 à vers 168) Le produit des diagonales est égal à la somme des produits des côtés opposés: mn = ac + bd Autres relations	Si m = x + y et n = v+ w, segments par rapport au point d'intersection, alors: xy = vw
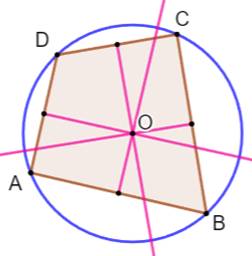
Propriétés des médiatrices Les quatre médiatrices des côtés se coupent au centre du cercle circonscrit. Condition nécessaire et suffisante pour que le quadrilatère soit cyclique. Explication Les segments OA, OB, OC et OD sont des rayons, donc de même longueur. Le point O est équidistant des sommes A et B, il est situé sur la médiatrice du côté AB. Idem pour les autres côtés.

Voir Toutes les relations

Aire du quadrilatère cyclique		haut
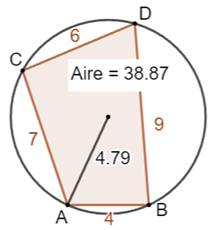
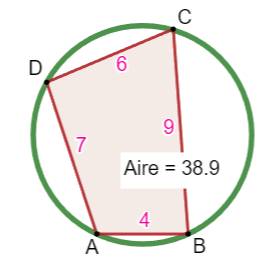
Propriétés des diagonales Si s désigne le demi-périmètre Voir Démonstration Exemple S = (4 + 9 + 6 + 7) / 2 = 13

Voir Formule de Bahmagupta

Rayon du cercle circonscrit		haut
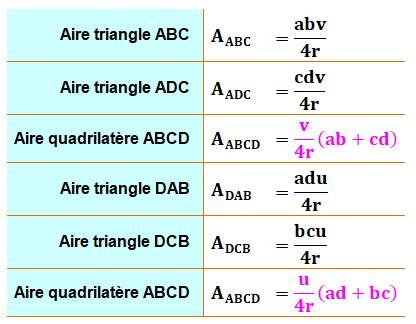
Double évaluation de l'aire du quadrilatère
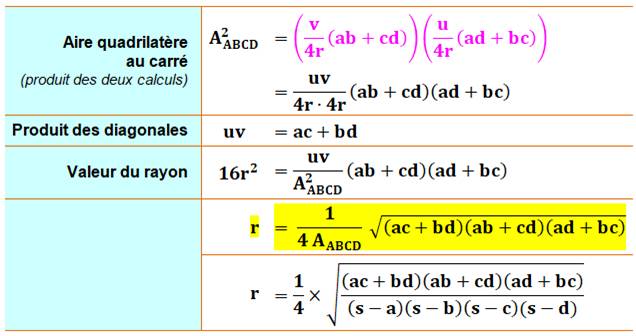
Rayon comme fonction de l'aire
Exemple

Médiane-hauteur (midpoint-altitude)		haut
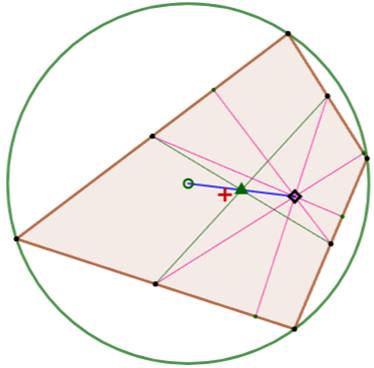
Sur cette figure: Le petit cercle vert est le centre du grand cercle; Le triangle vert est le centre de gravité des sommets du quadrilatère, c'est le point d'intersection des bimédianes vertes. Le losange noir est le point de concours des quatre droites issues du milieu d'un côté et perpendiculaires au côté opposé (un mix de médiane et de hauteur). Théorème de Jules Mathot (1901) Ces trois points sont alignés et le centre de gravité des sommets est au milieu. Centres de gravité Il s'agit bien, dans ce cas, du centre de gravité des quatre sommets, dit centre géométrique du quadrilatère. Le centre de gravité du quadrilatère (en pleine surface) est désigné par la croix rouge.

Cercles internes		haut
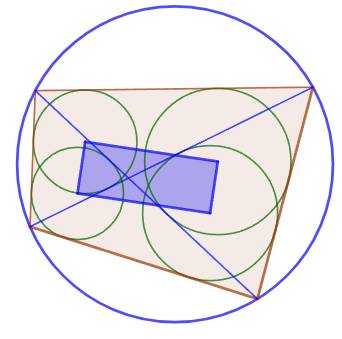
Sur cette figure: Le quadrilatère est inscrit dans le cercle bleu. Les quatre cercles verts sont inscrits dans les grands triangles internes au quadrilatère. Le quadrilatère ayant ces quatre centres pour sommets est un rectangle. Anglais: les quatre sommets du rectangle sont appelés incenters

Anglais

A cyclic quadrilateral means a quadrilateral that is inscribed in a circle. That means there is a circle that passes through all four vertices of the quadrilateral.

The vertices are said to be concyclic.

Étymologie

Le mot cyclique vient du mot grec kuklos , qui signifie cercle ou roue.

Le mot quadrilatère est dérivé du mot latin ancien quadri, qui signifie quatre et latus qui signifie côté.

Haut de page (ou double-clic)

Suite	Quadrilatères inscriptibles – Développements Points cocycliques
Voir	Allumettes Angles dans les polygones Carré Carré Carrés avec allumettes Carrés dans grille Carrés droits et carrés obliques – Quantité Carrés et rectangles sur l'échiquier Construction à la règle et au compas Constructions élémentaires: rectangle Dénombrer – Index DicoMot Maths	Énigmes classiques Ensembles – les compter Géométrie – Index Jeux – Index Le terrain de basket Losange Quadrilatères – Juniors Rectangles dans le cube Rectangles dans le rectangle Rectangles emboîtés Triangles dans triangles
Sites	Cercle inscriptible – Wikipédia Cyclic quadrilateral – Cuemath Cyclic quadrilateral – Wolfram Mathworld Incenters in Cyclic Quadrilateral: What is this about? – Cut-the-kno
Cette page	http://villemin.gerard.free.fr/GeomLAV/Carre/QuadAngl.htm