Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 09/02/2025 M'écrire Brèves de Maths

INDEX Défis en géométrie Géométrie Jeux et énigmes	Énigmes en géométrie
	Quatre carrés	Tête géométrique	Carré et 2 Trg Équilatéraux
	Exercices 01	Escalier dans cercle	Rect. et 2Trg Équilatéraux
	Carré et quarts de cercle	Carrés dans cercle	Triangle dans le cercle

Faites un double-clic pour un retour en haut de page

CERCLES & CARRÉS dans les quarts de cercle Résoudre cette énigme: quelle est la taille d'un cercle ou de deux cercles ou d'un carré inscrit au milieu de deux quarts de cercles ? Quelle est l'aire des zones courbes.
	Sommaire de cette page >>> Carré oblique dans quart de cercle >>> Carré dans le quart de cercle et demi-cercle >>> Un cercle et deux quarts de cercle >>> Deux cercles et deux quarts de cercle >>> Un carré et deux quarts de cercle >>> Aire des zones courbes	Débutants Géométrie Glossaire Géométrie

Carré oblique dans quart de cercle		haut
Problème tout simple à la mode Pythagore uniquement.
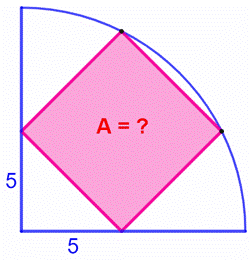
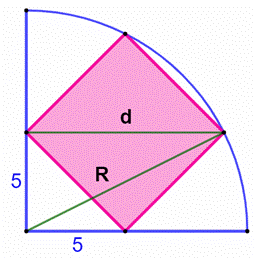
Construction Un quart de cercle et un carré inscrit dont deux des sommets sont à 5 cm du centre du cercle ; Quelle est l’aire du carré et le rayon du cercle ? Aire du carré Avec Pythagore, le côté du carré vaut : c² = 5² + 5² = 5√2 Aire du carré : Acarré = c² = 50 cm² Rayon du cercle Avec la diagonale du carré : d = c√2 = 5√2 × √2 = 10 cm Dans le triangle rectangle vert : R² = 5² + d² = 5² + 10² = 125 = 5 × 25 R = 5√5 = 11,1803… cm	Figure initiale Figure pour calcul du rayon

Voir DicoNombre 11,18

Carré dans le quart de cercle et demi-cercle		haut
Une petite construction pour y appliquer Pythagore ou, plus astucieux, une extension de construction.
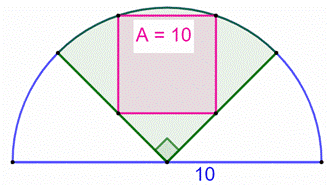
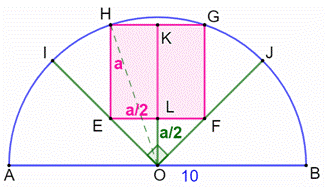
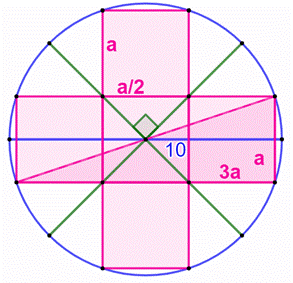
Construction Un quart de cercle (vert) dans lequel est inscrit un carré (rose). Cercle de diamètre 10 cm. Montrer que l'aire du carré vaut 10 cm². Pistes La bissectrice OK de l'angle droit IOJ partage le carré en deux rectangles de côtés (a et a/2). Les triangles EOF e ELO sont isocèles rectangles et : EL = LO = a/2. Côté a du carré Avec le théorème de Pythagore dans le triangle rectangle HKO : HO² = r² = 5² = (a/2)² + (a + a/2)² 4 × 25 = a² + 9a² = 10a² a² = 10 (aire du carré) a = √10 = 3,16 22 77 66 ...	Figure initiale Figure avec notations
Solution originale Le demi-cercle est complété et les carrés reproduit en quatre exemplaires, plus un carré au centre qui est isométriques aux autres (cf. triangles isocèles rectangles tels que vus ci-dessus). Considérons un rectangles formés de trois carrés et sa diagonale et appliquons de théorème de Pythagore : 10² = a² + 9a² = 10a² a² = 10	Nouvelle figure

Un cercle et deux quarts de cercle		haut
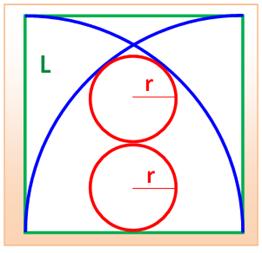
Construction Un grand carré bleu de côté L. Deux quarts de cercle dans ce carré. Quelle est la taille du cercle rouge inscrit dans l'espace entre les deux quarts de cercle en fonction de L ? Piste (Figure du bas) Le point T est le point de tangence du petit cercle et du quart de cercle Alors AT passe à la fois par le centre du petit cercle et celui du quart de cercle. La figure est symétrique et OH est axe de symétrie: AH = HB. Une évaluation des longueurs en fonction d r dans le triangle rectangle AOH permettra l'application du théorème de Pythagore. Calculs

Voir Brève 55-1089

Deux cercles et deux quarts de cercle		haut
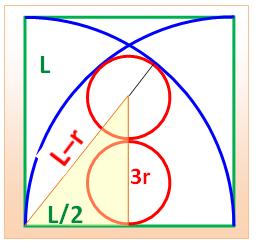
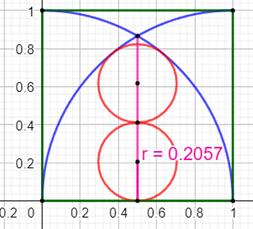
Construction Un grand carré bleu de côté L. Deux quarts de cercle dans ce carré. Quelle est la taille des deux cercles rouges de même rayon r inscrits dans l'espace entre les deux quarts de cercle en fonction de L ? Piste (Figure du milieu) Dessiner le triangle jaune et le prolongement de l'hypoténuse. Les côtés de ce triangle sont connus en fonction de r et L. Application du théorème de Pythagore. Calculs

Voir Équation du second degré

Un carré et deux quarts de cercle		haut
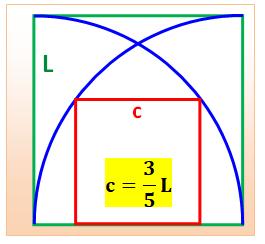
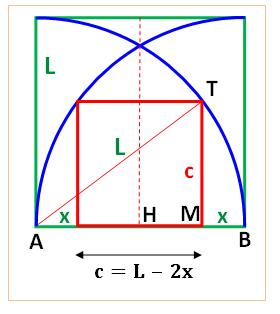
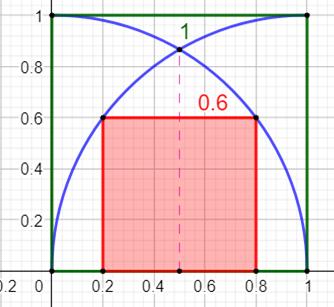
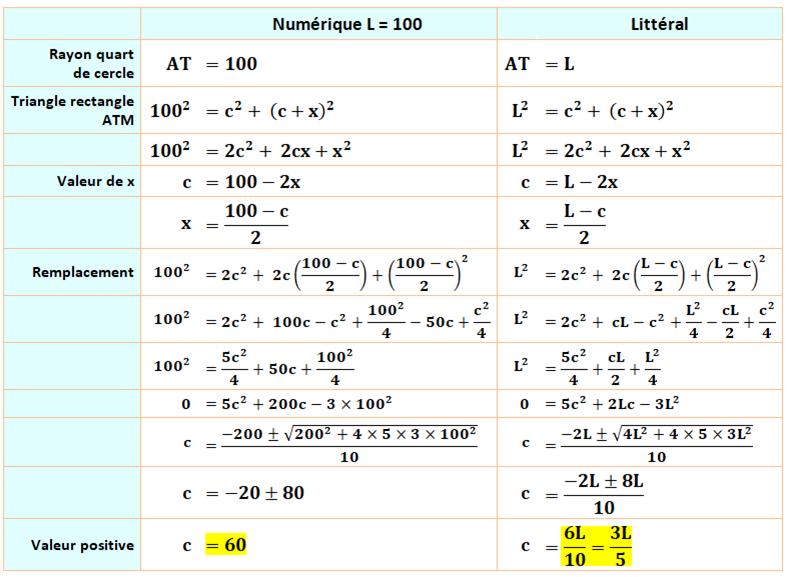
Construction Un grand carré bleu de côté 100 cm. Deux quarts de cercle dans ce carré. Quelle est la taille du carré rose inscrit dans l'espace entre les deux quarts de cercle ? Pistes: deux solutions Calculs avec géométrie Le segment AT est un rayon du quart de cercle (L) Nommons x la distance des sommets du carré aux pieds des quarts de cercle. Le côté du grand carré vaut: L = c + 2x. Données suffisantes pour appliquer le théorème de Pythagore dans le triangle rectangle ATM et résoudre la relation obtenue par rapport à c. 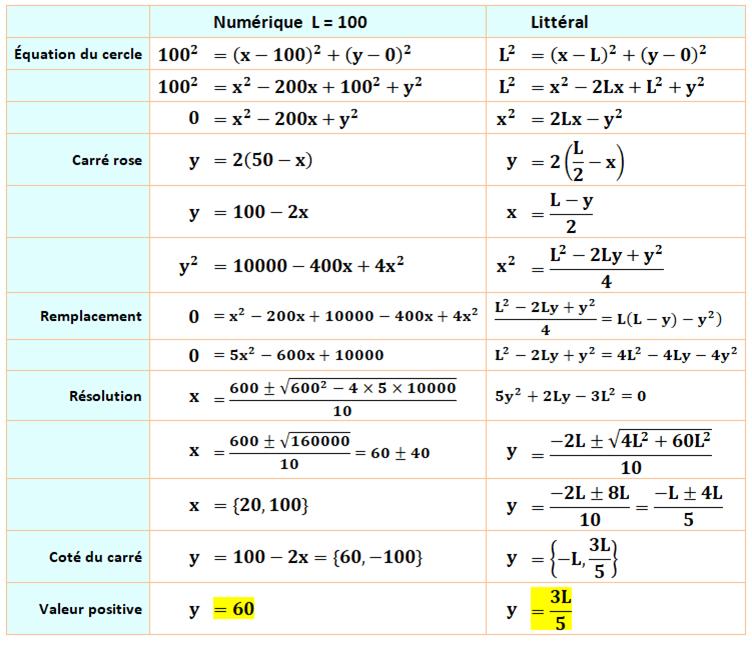Voir Calculs ci-dessous Calculs analytiques On note x et y les coordonnées du point M, l'un des sommets du carré rouge, lequel est situé sur l'un des quarts de cercle. Les coordonnées du point M sont connues en établissant l'équation du cercle. Si y = c est le côté vertical du carré, son côté horizontal mesure L – 2x. Ces deux valeurs, côtés du carré, sont égales. Voir Calculs ci-dessous
Calculs avec géométrie
Calculs analytiques

Illustration avec GeoGebra

Voir Brève 55-1089 / GeoGebra

Aire des zones courbes		haut
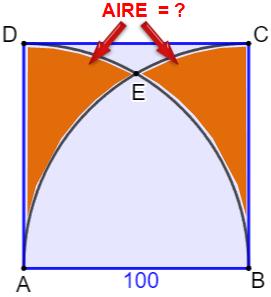
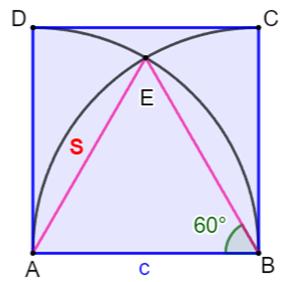
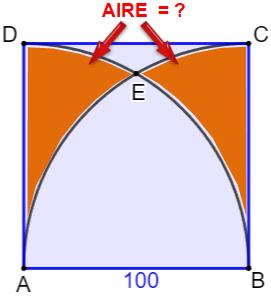
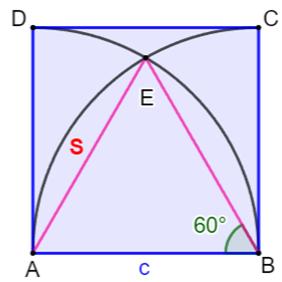
Construction Un grand carré bleu de côté c = 100 cm. Deux quarts de cercle dans ce carré. Quelle est l'aire des deux zones marron ? Piste L'aire d'une des zones marron est égale à celle du quart de cercle diminuée de deux fois l'aire S et diminué encore de l'aire du triangle équilatéral (AE = BE = AB = c = rayon des quarts de cercle). Calculs	Pour c = 100, A = 1712,1331… Ce qui représente17,12 …% de l'aire du carré.

Haut de page (ou double-clic)

Retour	Exercices sur le triangle – Niveau lycée Tête géométrique – Énigme Escalier dans cercle
Suite	Constructions élémentaires: triangle rectangle Résolution du triangle rectangle Doubler le triangle rectangle Quadrupler le triangle rectangle Triangles rectangles particuliers Types de triangles Triangle – Index
Voir	DicoMot Droite Égalités des triangles Enseignement – Collège Géométrie – Index Résolution du triangle quelconque Triangle de Pythagore
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Exercice/CarrQCer.htm