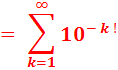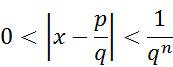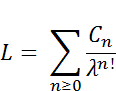|
||||||||||||||||||||||||||||
![]()
|
Liouville (1809-1882), mathématicien français.
Enseignant à Polytechnique. Prolixe avec plus de quatre cents publications.
C'est
Liouville qui, en 1842, présentera les travaux de Galois (1811-1832) à
l'Académie alors que d'autres, comme Cauchy, les avaient ignorés durant plus
de dix ans. |
Voir Contemporains
|
|
|
|
Nombre
transcendant de Liouville 0,11 000 1 00000 000000000000 1 000000000.... = 10-1! + 10-2!
+ 10-3! + 10-4! +...
Les "1" se trouvent en position
1, 2, 6, 24, 120 … = k! Soit, une multiplication de chacune par
2, 3, 4, 5 …
Back in 1844, Joseph Liouville came up with this number. He had successfully
made the first provable Transcendental Number. That number is now known as
the Liouville Constant. And it is a Liouville Number. |
|
|
|
|
|
Principe
de la démonstration de Liouville
Pour tout nombre entier positif n, il existe des entiers p et q, avec q > 1,
tels que:
|
|
|
|
|
|
|
|
|
|
|
|
Nombre
transcendant de Liouville-Erdös
LE =
0,21 0034 000059 000000716 00000001125
0000000001336 000…
LE3 = [LE x 10^3²] – [LE x 10^2²] x 10^5
= [LE x 10^9] – [LE x 10^4] x 10^5
= [200300005,0000007000…]
– [2003,000050000007000…] x 10^5
= 200300005 – 2003 x 10^5
= 200300005 – 200300000 = 5 |
|
![]()
|
Voir |
|
|
Pour
tous ceux qui veulent compléter leurs connaissances sur ce sujet et bien
d'autres. Très abordable. |
|
|
Cette page |
![]()