|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Carré magique 3 x 3 dit d'ordre 3
Carré magique
3 x 3 avec chiffres romains |
Oups! Je suis
novice
|
|
||
|
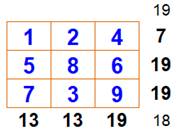
Il est unique ! (hors permutations)
|
Lignes 6 + 1 + 8 = 15 7 + 5 + 3 = 15 2 + 9 + 4 = 15 Colonnes 6 + 7 + 2 = 15 1 + 5 + 9 = 15 8 + 3 + 4 = 15 Diagonales 6 + 5 + 4 = 15 8 + 5 + 2 = 15 |
|
|
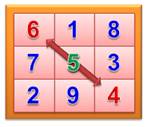
Notez La somme des sommets des quatre diagonales vaut 10 = 2
x 5, la valeur centrale.
|
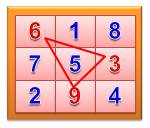
Remarquez également cette disposition en triangle:
6 = (9 + 3) / 2 8 = (7 + 9) / 2 4 = (7 + 1) / 2 2 = (1 + 3) / 2 |
|
|
Somme 1665 = 15 x 111 Les chiffres du carré magique sont concaténés en
nombres en ligne colonne, dans un sens et dans l'autre. Voir Nombre
1665 |
|
|
|
Somme des chiffres en ligne concaténés au
carré 618² + 753² + 294² = 1 035 369 816² + 357² + 492² = 1 035 369
|
Somme des chiffres en colonne concaténés
au carré 672² + 159² + 834² = 1 172 421 276² + 951² + 438² = 1 172 421 |
|
Voir
Calcul
de la somme magique / Son complémentaire / Ses huit variantes
|
|
|
|
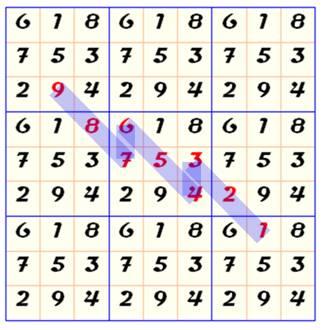
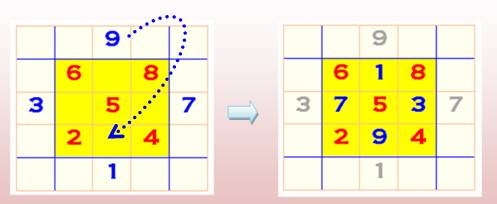
Alignement Reproduisons
le carré magique comme ci-dessous (tapis
magique).
C'est
magique, les nombres de 1 à 9 s'alignent en diagonale avec descente d'un cran
à chaque multiple de 3. Règle de construction géométrique du carré d'ordre 3 1)
Écrire les nombres en trois diagonales comme indiqué. 2)
Les nombres qui débordent sont "enroulés" sur le bord opposé (ou si
on préfère: décalés de trois crans vers l'intérieur du carré magique).
Effectivement:
en enroulant le feuillet jaune en cylindre
horizontal, on amènerait le 9 du haut dans la case du milieu en bas. |
|
Voir Méthode
du losange / Règles de
construction des carrés magiques / Symétries et
permutations
|
|
||||||||||||||||||||||||||||||
|
Normal
Tous les
chiffres de 1 à 9 |
Avec 0
Tous les
chiffres de 0 à 8 |
Et encore 0
Nombres de 1 à 10 |
||||||||||||||||||||||||||||
|
Pair
Nombres
pairs successifs |
Quelconque
N'importe
quels nombres |
Carré d'Allah
La somme
vaut 66, le nombre d'Allah |
||||||||||||||||||||||||||||
|
Somme première sur
lignes et colonnes
|
|
|||||||||||||||||||||||||||||
|
Total: 666, le
nombre de la Bête (Jaime
Ayala, Juin 1999, cité par De Geest) |
||||||||||||||||||||||||||||||
Rappel: chaque configuration est un exemple.
Toutes les permutations de lignes et
de colonnes sont permises.
|
|
|
|
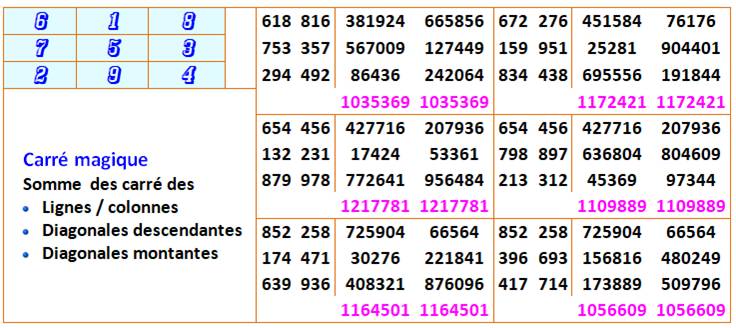
Dans un carré magique 3x3, la somme des carrés des
nombres formée en lignes est égale à la somme des carrés des mêmes nombres
retournés. Propriété valable pour les lignes, les colonnes et
toutes les (pan) diagonales.
Exemple de lecture: 618² + 753² + 294² = 381924 + 567009 + 86436 = 1035369 Le
calcul formel confirme cette
propriété pour toute permutation du carré3x3. Avec les notations
de Lucas, la somme des carrés en lignes, comme celle pour les retournés
donnerait: 36963 a² + 17982 b² – 22842
bc + 17982 c² |
|
Voir Brève
596
Voir Carrés magiques avec premiers / Nombres
premiers
|
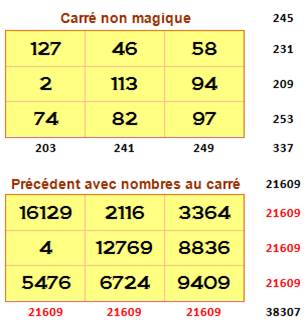
avec son retourné magique |
|
|
Le
plus petit carré magique tel que tous ses nombres étant retournés,
le carré reste magique et avec tous les nombres semi-premiers
(qui ont seulement deux facteurs hors 1 et le nombre)
|
|
|
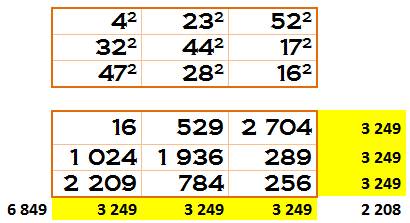
Carrés semi-magiques
d’ordre 3 avec des nombres au carré |
|
|
3 249 = 57²
21 609 = 174² Impossible d'obtenir un carré magique 3x3 complet avec
des carrés. |
|
Suite en Carrés magiques avec des nombres au carré
|
|
||||||||||||||||||||
|
Carré arithmétique
ou additif (en fait, normal) Carré magique des nombres de 0 à 8
Sommes constantes 1
+ 6 + 5 = 12 8
+ 4 + 0 = 12 etc. |
Carré géométrique ou
multiplicatif Carré magique des puissances de 2
Produits constants 2
x 64 x 32 = 4 096 256
x 16 x 1 = 4 096 etc. |
|||||||||||||||||||
|
Les
chiffres du premier sont utilisés comme exposants des puissances de 2 pour le deuxième: 21 = 2, 26 = 64, 25
= 32, etc. |
||||||||||||||||||||
Un carré magique 3 x3
avec des nombres nus
|
Le
plus petit carré magique d'ordre 3 avec des nombres nus (nombres divisibles par
chacun de leurs chiffres). Neuf nombres nus consécutifs non triviaux.
|
|
|
||
|
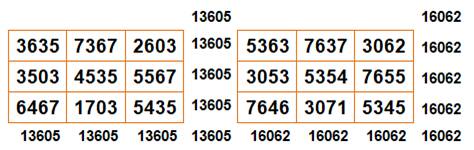
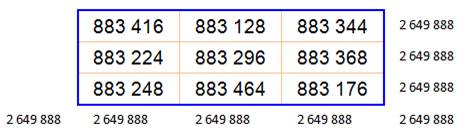
En
multipliant le carré initial par 1089, on
obtient évidemment un nouveau carré magique. Première propriété: chacun des chiffres pris
individuellement forme un nouveau
carré magique. Autres: toute combinaison de chiffres forme un
carré magique. |
Sommes magiques
15 et 16 335 |
|
|
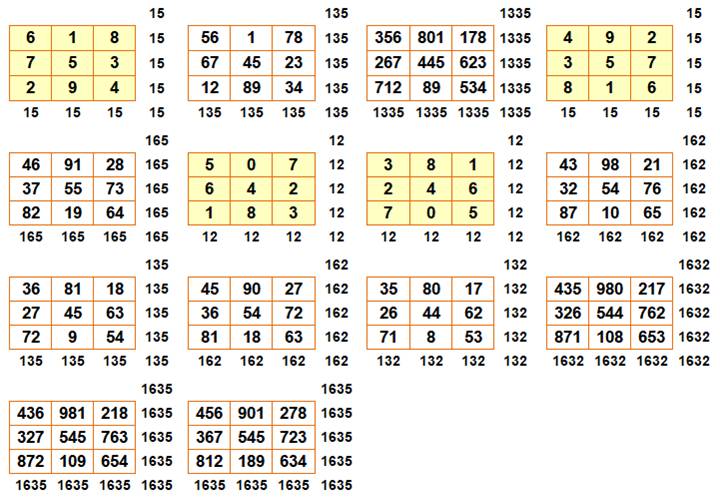
Les 14 configurations
magiques avec leurs sommes magiques
|
||
|
|
|
|
The unique normal
square of order three was known to the ancient
Chinese, who called it the Lo Shu. |
|
Henry Dudeney
publie ces carrés en 1917 dans son livre Amusements in Mathematics
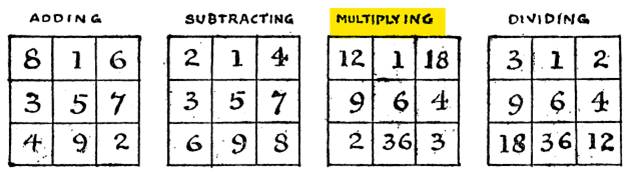
Voir Carrés magiques multiplicatifs
![]()
|
Suite |
|
|
|
Voir |
|
|
|
DicoNombre |
|
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/CMordre3.htm |
|
![]()
_________________________________________
Renvois de liens
Quantité de carrés magiques >>>
Somme des extrémités des diamètres >>>
Maths du carré magique 3 x 3
Propriétés du carré normal d'ordre 3 >>>
Forme générique des carrés magiques d'ordre 3 >>>
Autres
formes génériques >>>
Voir Propriétés des
carrés 3 x 3 / Construction du carré 9x9