![]()
|
|
Ce site est désormais accessible en http://diconombre.fr/index.html et
pour cette page voir le lien en fin de page For
this page, refer to the link at the bottom. |
|
22 Novembre 2025
![]()
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
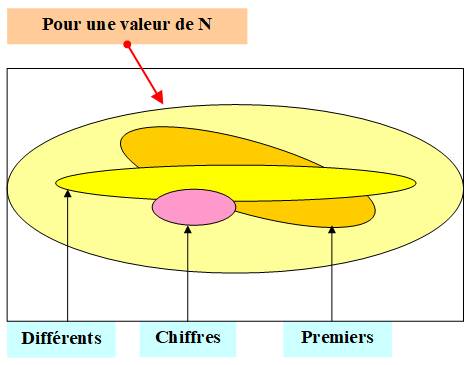
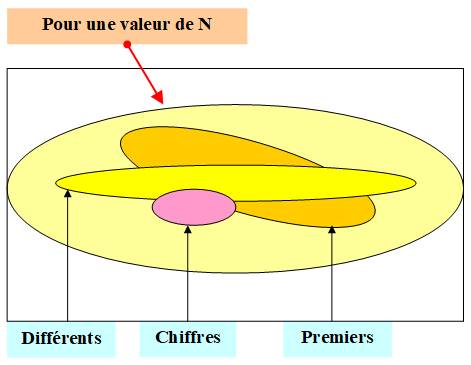
PARTITIONS particulières Comment s'y retrouver? |
|
|
Décomposition
particulières d'un nombre en sommes de nombres.
Aller
directement à l'index >>> |
Exemple de curiosités: cubes et chiffres
Voir Nombres et chiffres en puissance |
|
|
|
|
|
|
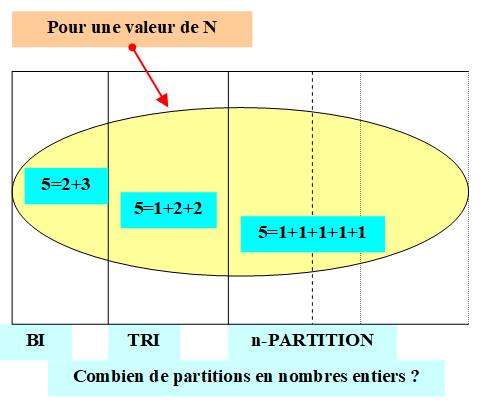
Voir Partitions
– En bref
|
|
|
|
Les
partitions
ENTIERS
- Partitions classiques
ENTIERS
- Partitions particulières
|
|
|
PUISSANCES
Computing Minimal Equal Sums Of Like Powers par
Jean-Charles Meyrignac |
Voir Puissance concaténation de
puissances
|
|
|
|
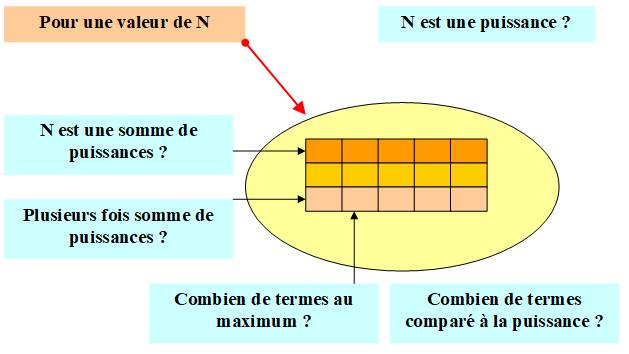
NOMENCLATURE
des problèmes posés avec des sommes de puissances Notations
25 = 5² = 3² + 4²
4 225 = 65² = 16² + 63² = 25 + 60² = 33² + 56² = 39² +
52² => (2 / 1, 2 / 4)
N => (p / n, m / q) |
|
|
Exemples de notations
Par
exemple:
Les triplets de Pythagore p = 2, n = 1, m = 2 (2 / 1, 2 / -) x 2 = y 2 + z 2 Autre
exemple: Le théorème de Fermat-Wiles dit que: Pour p > 2, n =
1 et m = 2 est impossible (p / 1, 2 / -) x p = y p + z p |
|
p = puissance,
valeur de l'exposant n = quantité de
termes à gauche m = quantité à
droite q = quantité de
sommes non triviales Exemple:
29 = 0² + 2² + 5² = 2² + 3² + 4² => (2 / 1,3 / 2) |
Note: pour les partitions classiques voir
l'index
|
p |
n |
m |
q |
Formulation |
Nom |
Liens |
|
|
|
|
|
|
|
|
|
1 |
n |
- |
q |
N = a1 +…+ an |
|
|
|
|
|
|
|
|
|
|
|
2 |
0 |
2 |
q |
N = a12 + a22 |
|
|
|
|
|
|
|
N = a12 - a22 |
|
|
|
2 |
1 |
2 |
q |
N = a12 = b12
+ b22 |
|
|
|
2 |
0 |
3 |
q |
N = a12 + a22 + a32 |
|
|
|
2 |
1 |
n |
1 |
N = a12 =
b13 + b23 + … |
|
|
|
2 |
0 |
4 |
|
N = a12 + … + a42 |
|
|
|
2 |
|
|
|
N = n² + (n+1)² + … |
|
|
|
|
|
|
|
|
|
|
|
3 |
0 |
2 |
q |
N = a13 + a23 |
|
|
|
3 |
0 |
3 |
q |
N = a13 + a23 + a33 |
|
|
|
3 |
1 |
3 |
q |
N = a13 =
b13 + b23 + b33 |
|
|
|
3 |
|
|
|
N = n² + (n+1)² + … |
|
|
|
|
|
|
|
|
|
|
|
5 |
1 |
|
|
N = a15 + a25 + a35
+… |
|
|
|
5 |
1 |
5 |
|
N = a15 + a25 +... + a55 |
|
|
|
5 |
1 |
5 |
|
N = a15 – a25 +... + a55 |
|
|
|
|
|
|
|
|
|
|
|
p |
n |
0 |
- |
N = a1p +…+ anp
|
|
|
|
p |
n |
0 |
- |
N = a1p +…+ anp
|
|
|
|
p |
n |
0 |
q |
N = a1p +…+ anp
avec q max |
|
|
|
p |
n |
0 |
q |
N = a1p +…+ anp
avec p = 1 à q |
|
|
|
|
|
|
|
|
|
|
|
p |
n |
m |
- |
N = a1p +…+ anp = b1p +…+
bmp |
|
|
|
p |
1 |
2 |
- |
N = x p = y p + z p |
|
|
|
p |
n |
n |
- |
|
|
|
|
p |
p |
p |
- |
N = a1p +…+ app = b1p +…+
bpp |
|
|
|
p |
p+1 |
p+1 |
- |
|
|
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites sur les
sommes de puissances
|
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Addition/PttSyret.htm
|
![]()