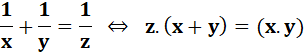NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 13/02/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Type de nombres
Débutants Général	FRACTIONS				Glossaire Fraction
INDEX Calcul	Débutant	Unitaire	Continues	Égyptiennes
	Comparaison	Règle de trois	Somme 1	Glouton
	Construction	Illicites	Inverse	Identités
			Puissances
		Sommaire de cette page >>> Amusement >>> Approche >>> Propriétés >>> Illustration amusante >>> Solution de l'équation 1/x + 1/y = 1/z >>> Complexe >>> Densité de fractions >>> Anglais

FRACTIONS ÉGYPTIENNES

Fractions dont le numérateur vaut toujours 1. Seules exceptions 2/3 et sans doute 3/4. En tout cas ces deux fractions étaient chacune représentée par un hiéroglyphe.

On ne sait pas très bien pourquoi les Égyptiens en étaient venus à utiliser ces fractions. Aujourd'hui, elles sont propices à des jeux. Notamment, comment découper une tarte en parts toutes inégales? …

Amusement
Quatre enfants sont bien empruntés. Ils n'ont que trois biscuits à se partager. Comment faire? Chacun aura bien entendu 3/4 de biscuit. Comment faire le moins de découpes? Il suffit de partager d'abord en moitiés. Chacun une. Puis de partager le troisième en quarts. Chacun un.	Avec 3 biscuits pour 4 enfants, chacun aura ½ et ¼ .

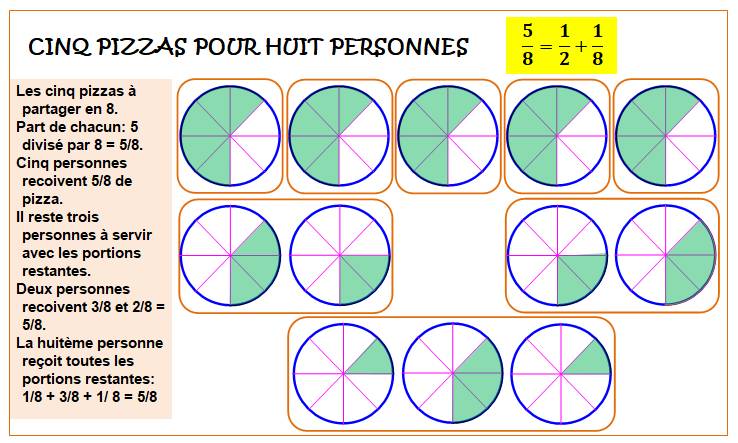
Un cas un peu plus délicat

Approche
Cette fraction égyptienne a été trouvée sur le papyrus Rhind, inscrite par le scribe Ahmes il y a 3500 ans.	= 0,1176...
Fraction égyptienne: le numérateur est toujours égal à 1, à l'exception des fractions 2/3 et 3/4. somme de fractions unitaires avec dénominateurs tous différents. Fraction unitaire: numérateur égal à 1, et le dénominateur est un entier positif.	Exemples = 0,75 Non égyptienne. Trop simple! Trivial. = 0,9444…

Exemples

2/7	= 1/4 + 1/28
2/11	= 1/6 + 1/66
2/97	= 1/56 + 1/679 + 1/776
Etc.

Mais:

7/10	= 2/3 + 1/30

On conjecture que 4/n et 5/n

sont décomposables en somme de trois fractions unitaires.

CONSTRUCTION
Formule de base => En 1201, Fibonacci trouve un algorithme, dit algorithme glouton.	Suite en Construction des fractions unitaires et égyptiennes.

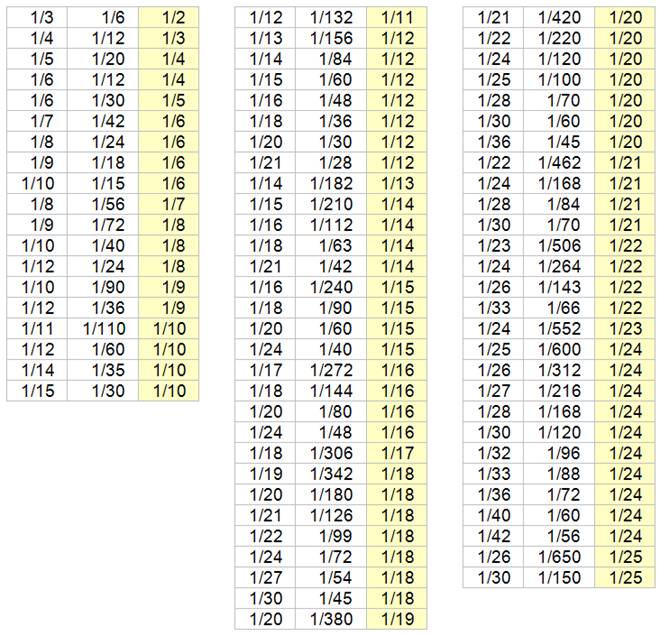
Voir Table et comparaison entre fractions usuelles

Propriétés

Deux fractions exprimées sous forme égyptienne sont plus facilement comparables. Exemple La différence entre ce deux fractions est 3/56 = 0,05 … Tout nombre rationnel positif peut être exprimé en fraction égyptienne et ce, d'une infinité de façons différentes (cf. procédé de construction). La somme des fractions égyptiennes consécutives est supérieure à n'importe quel nombre, pourvu que le nombre de termes soit assez grand: Série lentement divergente, mais… divergente. La question du plus petit dénominateur final pour la plus petite quantité de termes est un sujet qui est très ouvert. Voir Denser Egyptian fractions notamment par Greg Martin

Illustration amusante

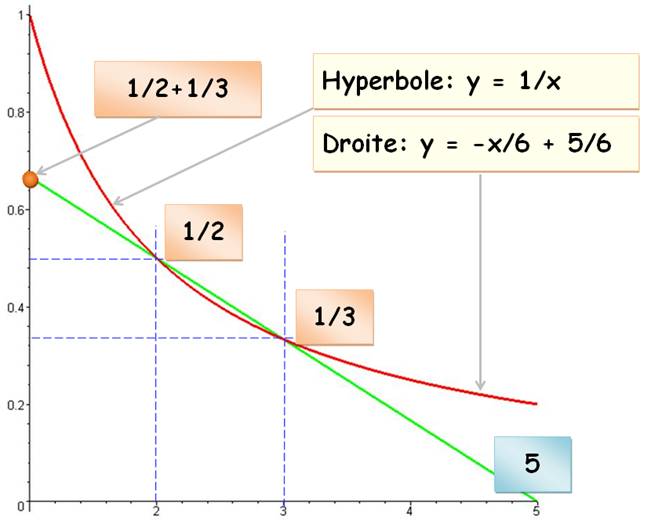
Voir Explications / Hyperbole

Solution de l'équation 1/x + 1/y = 1/z
Trouver les solutions de cette équation diophantienne revient à chercher quels sont les nombres dont le produit (x.y) vaut z fois la somme. Exemple: 1/3 + 1/6 = 1/2 & 2 (3+6) = 3x6 = 18 Liste des 77 solutions pour z jusqu'à 25 et x et y jusqu'à 1000:

Nombres complexes
Avec les nombres complexes. Souvenez-vous que: (2-i)(2+i) = 2² + 2i – 2i – i² = 5 Voici quelques exemples de valeurs pour:	a b F F 2 1 4/5 0,8 3 1 3/5 0,6 1 2 2/5 0,4 4 2 2/5 0,4 4 3 8/25 0,32 2 3 4/13 0,30769… 6 2 3/10 0,3 7 1 7/25 0,28 3 4 6/25 0,24 1 3 1/5 0,2 2 4 1/5 0,2 8 4 1/5 0,2 9 3 1/5 0,2 6 6 1/6 0,1666… 8 6 4/25 0,16 10 5 4/25 0,16 3 6 2/15 0,1333… 6 8 3/25 0,12 1 4 2/17 0,1176… 2 6 1/10 0,1 4 8 1/10 0,1 3 9 1/15 0,0666… 2 8 1/17 0,0588…

Densité de fractions

Deux exprimé par une somme de 366 fractions égyptiennes avec un dénominateur inférieur à 1000.

2 = 1/13 + 1/19 + 1/23 + 1/27 + 1/29

+ 1/32 +1/34 + 1/35 + 1/36 + 1/38 + 1/39

+ 1/40 + 1/42 + 1/44 + 1/45 + 1/46 + 1/49 + 1/50 +

 …

+ 1/950 + 1/952 + 1/957 + 1/960 + 1/966 + 1/969 + 1/975

+ 1/980 + 1/986 + 1/988 + 1/990 + 1/992

Conséquence
Il est possible de diviser 2 tartes en 366 parts inégales.

Avec le nombre 1, il y a 454 telles fractions:

1 = 1/97 + 1/103 + 1/109 + … + 1/996 + 1/999

Valeurs entières possibles de N

N	Avec n	Faisable?
2	< 1 000	Possible (voir ci-dessus)
8		Impossible
3 à 7	< 1000	Pas impossible; pas encore connu
Entier	n quelconque	0,3 n possibilités au maximum
2	= 1 000 000	Probablement 300 000 fractions

Recherche

Travaux récents (1998) des mathématiciens Greg Martin et Ernest Croot: " Comment exprimer un entier sous la forme du plus grand nombre possible de fractions égyptiennes différentes." 

Anglais: Dense Egyptian fractions
Voir Greg Martin University of British Columbia (maths avancées)

English corner

The ancient Egyptians (1650 av. J.-C.), as far as we can tell from the documents now surviving, used a number system based on unit fractions: fractions with one in the numerator. They wrote positive rational numbers as sums of distinct reciprocals of positive integers, or unit fractions. An Egyptian fraction is a sum of positive (usually) distinct unit fractions. In 1202, Fibonacci published an algorithm, subsequently rediscovered by Sylvester in 1880, among others, for constructing such representations, which have come to be called Egyptian fractions, for any positive rational number.

Suite	Algorithme pour la recherche des fractions égyptiennes Comparaison des fractions usuelles Construction de ces fractions Énigme du partage des 11 bonbons Énigme du partage des 17 chevaux Fractions – Glossaire et index Suite de Sylvester Nombres semi-parfaits primaires
Voir	Inverse d'un nombre Tables des fractions égyptiennes Fraction avec 0,65 Fractions dont la somme est égale à 1 Sommes d'inverses Théorie des nombres – Index
DicoNombre	Nombre ¼ Nombre 1/3 Nombre ½ Nombre 2/3 Nombre ¾ Nombre 3/7
Cette page	http://villemin.gerard.free.fr/Calcul/Fraction/Egyptien.htm
Sites	Fractions égyptiennes sur Wikipédia Site de Dr Ron Knott (anglais)