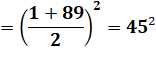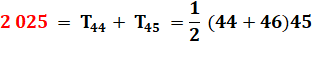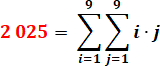Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Création du: 14/10/2024 Édition du: 22/03/2025 M'écrire Brèves de Maths

DicoNombre Débutant Glossaire Types de nombres Nombres géométriques Nom des nombres Écriture des nombres Table des facteurs Nombres et anglais Langues	Dictionnaire des Nombres
	1 / 10 / 50 / 100 / 500 / 1000 / 1500 / 1900 / 2000 / 2016 / 2017 / 2018 / 2019 /	2025	2031 à 2099 / 3000 / 5000 / 10 000 / 20 000 / 50 000 / 100 000 / 10^6 / 10^9 / 10^100 Autres
	2020 / 2021 / 2022 / 2023 / 2024 / 2025 / 2026 / 2027 / 2028 / 2029 / 2030

Index 2025 – ONZE pages pour ce nombre exceptionnel

Nombre 2025	En bref, culture et calendrier	Nombre 2025 en 20 diapos
Numération et chiffres	Additions et soustractions	Multiplications, divisions, diviseurs
Puissances	Nombre géométrique	Jeux, dénombrement et curiosités
Actualités	Humour 2024-2025	Chiffres de 2025 (jeu)

Faites un double-clic pour un retour en haut de page

Addition

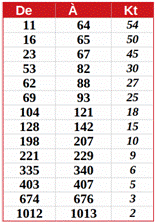
2 025 = 11 + 12 + … + 64 = ... = 1012 + 1013			Nombre 14-poli Car quatorze fois somme de nombres consécutifs. Pour le premier, de 11 à 64, il y a 54 nombres. Voir Toutes les sommes explicitées
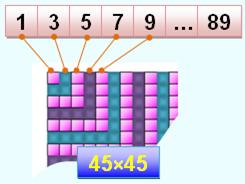
2 025 = 1 + 3 + 5 + … + 89		Somme de 45 nombres impairs successifs.
		Somme de deux nombres triangulaires consécutifs. Identité comportant trois nombres consécutifs.
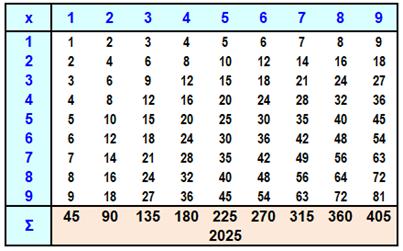
qui se lit: somme des produits des nombres i et j pour tous les j de 1 à 9 et pour tous les i de 1 à 9. Sur la table La somme de la première colonne vaut: 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45 La somme des colonnes successives valent: 45×1, 45×2, 45×3 …, 45×9 Leur somme devient: 45 (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9) = 45 × 45 = 2025		Somme des nombres de la table de multiplication des nombres de 1 à 9. Table de multiplication Voir Jolie animation par Vincent Pantaloni

Partitions

952921 1130228034 7993958546 3291227245 7677896880 = 9,52… 10^45		Quantité de partitions du nombre 2025. Oui! on peut écrire autant d'additions qui auront 2025 pour somme.
2 025 = 1597 + 377 + 34 + 13 + 3 + 1		Partition de Zeckendorf, c.a.d. avec des nombres de Fibonacci. Le théorème de Zeckendorf affirme que tout nombre entier naturel peut s'écrire de manière unique comme une somme de nombres de Fibonacci non nuls et distincts, en imposant la condition que deux nombres consécutifs dans la suite de Fibonacci ne soient pas employés simultanément.
2 025	N'est pas la somme de deux premiers. Ce qui n'est pas si courant pour un carré. Voir Conjecture de Goldbach
1 013 352 947	Quantité de partitions de 2025 avec uniquement des 1 et des 2. Idem avec les 3 en plus.
340 707	Quantité de partitions de 2025 à trois termes distincts.
2 025	Quantité de partitions de 45 avec au moins trois termes distincts. Programme Maple permettant de tester ce genre de propriété La condition "if" teste si la partition comporte plus de deux termes (q>2) et si les termes sont tous différents. Voir Programmation – Index

SUITE SUR LE NOMBRE 2025 voir index en Haut de page (ou double-clic)

Retour	Nombre 2024 Nombre 2023 Nombre 2022 Nombre 2021
Suite	Nombre 2025 en 20 diapos Vœux et humour Noël 2024 – Nouvel an 2025 Jeu avec chiffres de 2025 Énigmes virales Nombre 2026 Nombres de 2030 à 2099 Nombres de 2100 à 2299
Sites	2025, un nombre très carré – Tangente 221 – Fabien Aoustin et Michel Criton 2024+1 (Cette nouvelle année est intéressante) Numbers Aplenty 2025 Année 2025 – Wikipédia What are the interesting ways to write 2024 … - Mathematics 5 Fun Facts About 2025 You Probably Don't Know – Mind your decision – Inder J. Taneja
Cette page	http://villemin.gerard.free.fr/NombDico/N1000/N20252.htm