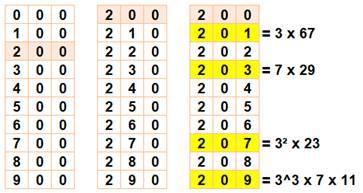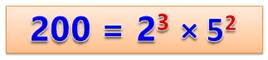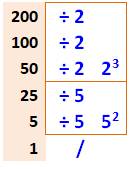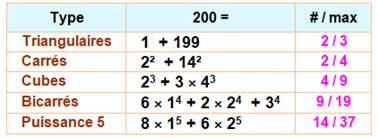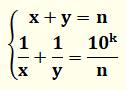|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
BRÈVES de MATHS – Page 42 Un millier de faits et chiffres sur les nombres et les
mathématiques
En principe ces pages sont très abordables sans
connaissances particulières de maths. Elles sont proposées dans un ordre
quelconque favorisant la découverte de sujets multiples. |
Anglais: Facts and figures about numbers and mathematics
Page spéciale dédiée au NOMBRE 200
et à quelques notions de la THÉORIE
des NOMBRES
820. Nombre 200 – Langues |
|
||
|
En français 200 Deux-cents, deux-cent-un, trois-cents,
trois-cent-un. Traits d'union partout; pas de pluriel à cent si
suivi d'un nombre. 200e Deux-centième, deux-cent-unième. Deux-cents fois: ducenties du lation duo centum Bicentenaire. Il était aux deux-cents coups – He's frantic |
Autres langues Two hundred Anglais Zweihundert Allemand Doscientos Espagnol Duemila Italien Dois Mil Portugais |
||
|
Brèves associées |
>>>
Nombres dans les mots français |
>>>
Brèves Langue – Index |
|
|
Pour en savoir plus |
>>>
Nombre 200 dans le DicoNombre |
>>>
Nouvelle orthographe des nombres |
|
821. Nombres pairs et cousins |
|
|||
|
Pair et impair Le nombre 200 est divisible par 2, c'est un
nombre pair. Les nombres non-divisibles
par 2 sont impairs: ils produisent un
reste égal à 1. Pairs et impairs, on leur donne une forme
générique:
Pratique pour faire certains calculs. Exemple
|
Généralisation En théorie des nombres, il est parfois utile de
restreindre le terrain de jeu: ne pas utiliser tous les nombres jusqu'à
l'infini, mais les "enrouler" dans un domaine plus limité.
Les mathématiciens utilisent ce procédé avec le
2, le 12 et tous les autres nombres et appellent cela le calcul modulo. Exemple
|
|||
|
Brèves associées |
>>>
Parité
des puissances >>>
Exemple de calcul modulo |
>>>
Brèves Théorie – Index |
||
|
Pour en savoir plus |
>>>
Nombres pairs et impairs |
>>>
Calcul modulo |
||
822. Nombres composés et premiers |
|
|||
|
Nombres composés Le nombre 200 est divisible
de manière évidente par 2 et par 5.
Tous les nombres divisibles par un autre sont des
nombres composés. Image Un nombre composé correspond à l'aire d'un
rectangle ayant des longueurs entières. Pour représenter le nombre 200, on pense, par
exemple, à un rectangle de longueur 20 et de largeur 10, et son aire est bien
200. |
Nombres premiers Il existe des nombres sans possibilité de
divisibilité. Par exemple, il est impossible de partager le nombre 199 en k parts égales. Ce sont des nombres premiers.
La liste commence comme ceci: Les nombres premiers sont répartis sans ordre
connu. Ce qui veut dire qu'il n'existe pas de formule pour les définir. Cependant, ils sont tous voisins d'un multiple de
6 comme le montre cette barre magique. |
|||
|
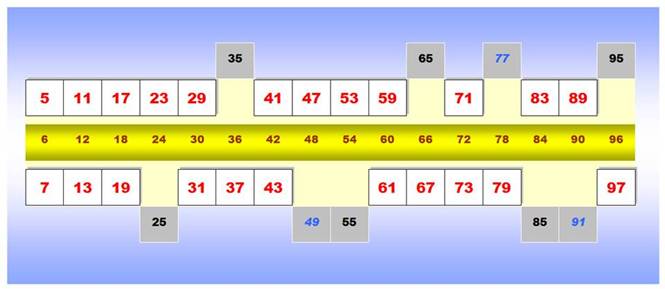
Barre magique des nombres premiers
inférieurs à 100 (hors 2 et 3)
Au milieu, en jaune, les multiples de 6; Au-dessus et en dessous, en rouge, les nombres
premiers, tous voisins des multiples de 6. En bordure, en gris, les exceptions. |
||||
|
Brèves associées |
>>>
Nombres premiers |
>>>
Brèves Types – Index |
||
|
Pour en savoir plus |
>>>
Nombres premiers >>>
Nombres composés |
>>>
Divisibilité par … |
||
823. Composé stable (jamais premier) |
|
|||
|
Composé stable Ici, on cherche à déstabiliser le nombre en
modifiant l'un de ses chiffres. Le tableau de droite montre tous les nombres
formés à partir de 200 en changeant le premier chiffre, ou le deuxième ou le
troisième. Tant que le nombre modifié est terminé par un 0,
il est composé. En modifiant le chiffre des unités, on trouve:
En fait, ils sont tous composés. Le nombre 200
est un nombre composé stable. |
Le nombre 200
Les
suivants sont: 204, 206, 208, 320, … |
|||
|
Brèves associées |
>>>
Nombres
composés – Record de suite |
>>>
Brèves Type – Index |
||
|
Pour en savoir plus |
>>>
Nombres composés |
>>>
Nombres premiers – Index |
||
824. Facteurs et diviseurs |
|
|||
|
Facteurs
Tout nombre peut être décomposé en un produit de
nombres premiers de façon unique, aux permutations près.
Pour trouver les facteurs, le
nombre est divisé par 2, puis par 3, puis par 5, etc. et cela, autant de fois
qu'il est possible comme le montre le dessin. |
Diviseurs Ce sont tous les nombres qui divisent exactement
le nombre 200. Ils sont douze en comptant 200: Ceux-ci sont symétriques. Voyez ces produits: La quantité de
diviseurs d'un nombre est calculée simplement en faisant le produit des
exposants plus 1: La somme
utilise également les exposants:
|
|||
|
Brèves associées |
>>>
Nombre 100 |
>>>
Brèves Nombres – Index |
||
|
Pour en savoir plus |
>>>
Facteurs et diviseurs |
>>>
Somme des diviseurs |
||
825. Nombre puissant |
|
|||
|
Nombres puissants Dans l'expression de la factorisation du nombre,
ce sont les exposants {3 et 2} que
nous observons. Ils sont tous les deux supérieurs à 1, on dit que
ce type de nombre est un nombre puissant. Ils ne sont pas égaux: 200 n'est pas une puissance pure comme l'est, par exemple: 100 =
2² × 5². Plus petit nombre d'Achille: 72 = 23 ×
32. |
Le nombre 200 est
un nombre d'Achille
Exposants
différents et supérieurs à 1. Nombres d'Achille
jusqu'à 1000 72, 108, 200, 288, 392, 432, 500, 648, 675, 800,
864, 968, 972, 1125, … |
|||
|
Brèves associées |
>>>
Nombres
proniques |
>>>
Brèves Types – Index |
||
|
Pour en savoir plus |
>>>
Nombres puissants >>>
Nombres d'Achille |
>>>
Puissance et exposants |
||
826. Nombre abondant et voisins |
|
|||
|
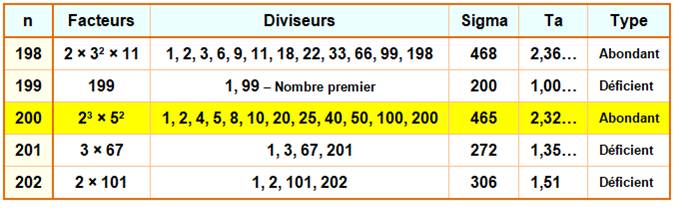
Abondant On cherche ici, les propriétés des nombres en
fonction de la somme de leurs diviseurs (sigma). Ce nombre dépasse le double de 200. On dit que le
nombre 200 est abondant et que son taux d'abondance est 465 / 200 = 93 / 40 = 2,325… Parfait Il existe des nombres particuliers dont le taux
d'abondance est exactement 2, ce sont des nombres parfaits,
comme le nombre 6: |
Déficient Pour certains nombres, le taux
d'abondance est inférieur à 2 (ou à 1, si on retirait le nombre de la somme des
diviseurs). C'est le cas de tous les nombres
premiers dont la somme des diviseurs vaut P + 1: On dit que ces nombres sont déficients. Le nombre suivant: 201 = 1 x 3 x
67 a pour somme des diviseurs: 1 + 3 + 67 + 201 = 272 |
|||
|
Autour du nombre
200
|
||||
|
Brèves associées |
>>>
Nombre abondants, … |
>>>
Brèves Types – Index |
||
|
Pour en savoir plus |
>>>
Abondant, Parfait ou Déficient |
>>>
Nombres parfaits |
||
827. Nombres amis |
|
||
|
Amis et solitaires On connait le taux d'abondance du nombre 200
(somme des diviseurs divisée par le nombre): 93 / 40. On cherche d'autres nombres qui posséderaient ce
même taux. Le nombre 80 répond à ce critère. Les nombres 80 et 200 forment une paire d'amis. Il existe des chaines d'amis: 30,
140, 2 480, 6 200, 40 640, … Les nombres sans
amis sont les nombres solitaires. |
Les nombres 80 et
200 sont amis
Sigma est la somme des
diviseurs. |
||
|
Brèves associées |
>>>
Nombres
amicaux |
>>>
Brèves Types – Index |
|
|
Pour en savoir plus |
>>>
Nombres amis et nombres solitaires |
>>>
Nombres amicaux |
|
828. Nombre semi-parfait |
|
||
|
Semi-parfait Nous venons de voir qu'un nombre parfait est tel que la somme de ses diviseurs et
le double du nombre. Un nombre semi-parfait
suit cette logique, mais avec la somme d'un jeu des diviseurs. Le nombre 200 est douze fois égal à la somme
partielle des diviseurs comme le montre le tableau. On peut aussi s'intéresser à la somme des
inverses des diviseurs: notion de semi-parfaits primaires. |
Somme 200
|
||
|
Brèves associées |
>>>
Nombres
S-parfaits |
>>>
Brèves Types – Index |
|
|
Pour en savoir plus |
>>>
Nombres semi-parfaits |
>>>
Semi-parfaits primaires |
|
829. Nombre pratique |
|
||
|
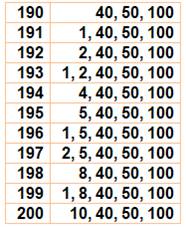
Nombre pratique Encore une utilisation des diviseurs de 200. Tous les nombres jusqu'à 200 peuvent s'exprimer
comme une somme d'un jeu de diviseurs de 200, comme le montre le tableau pour
les nombres de 190 à 200. Le nombre 200 est un nombre pratique. Seuls les nombres pairs sont pratiques. Parmi les premiers pairs, les suivants ne sont pas pratiques: 10, 14, 22, 26, 34, 38, 44, 46, 50, … |
|
||
|
Brèves associées |
>>>
Nombres
intouchables |
>>>
Brèves Types – Index |
|
|
Pour en savoir plus |
>>>
Nombres pratiques |
>>>
Tableau complet pour 200 |
|
830. Opérations avec les chiffres |
|
|||
|
Souvent un amusement, ici, on cherche des
configurations particulières avec les chiffres. Le nombre 200 est banal de ce point de vue. |
Exemple de configurations 513 + 315 = 828 Ce nombre devient palindrome
en lui ajoutant son retourné. 513 + (5 × 1 × 3) = 528 = 1 + 2 + 3 + … + 32 Ce nombre devient triangulaire
en lui ajoutant le produit de ses chiffres. |
|||
|
Brèves associées |
>>> Palindromes |
>>>
Brèves Motifs – Index |
||
|
Pour en savoir plus |
>>>
Nombres retournés |
>>>
Nombres palindromes >>>
Nombres triangulaires |
||
831. Somme des chiffres |
|
||
|
Nombres et chiffres On rappelle la différence entre chiffres et
nombres:
Nombres de Harshad Le nombre 200 est un nombre de Harshad bien banal (en maths, on dit trivial).
Il est divisible par la somme de ses chiffres: 200 / (2+0+0) = 100. Il existe des nombres de Harshad amusants: la
somme se retrouve dans le nombre: |
Nombres de Harshad jusqu'à 200 1, 2, 3, 4, 5, 6, 7, 8, 9,
10, 12, 18, 20, 21, 24, 27, 30, 36, 40, 42, 45, 48, 50, 54, 60, 63, 70, 72,
80, 81, 84, 90, 100, 102, 108, 110, 111, 112, 114, 117, 120, 126, 132, 133,
135, 140, 144, 150, 152, 153, 156, 162, 171, 180, 190, 192, 195, 198, 200 … Le nombre 200 est aussi
divisible par 4, soit deux fois la
somme de ses chiffres: c'est un nombre de Niven. |
||
|
Brèves associées |
>>>
Nombres à
chiffres concaténés |
>>>
Brèves Types – Index |
|
|
Pour en savoir plus |
>>>
Nombres de Harshad |
>>>
Nombres de Friedman |
|
832. Nombre fourchette |
|
||
|
Encore une propriété dépendante des chiffres du
nombre. On forme le nombre à 2k chiffres dont:
Avec 200 et k
= 1, on forme 20. Le nombre est
fourchette (ou gapful en anglais) si ce nouveau nombre divise le nombre
d'origine. Le nombre 200
est un nombre fourchette. |
Un exemple de nombre fourchette avec k = 2
Ce nombre
est divisible par le nombre sans ses chiffres centraux. |
||
|
Brèves associées |
>>>
Nombres à
chiffres concaténés |
>>>
Brèves Types – Index |
|
|
Pour en savoir plus |
>>>
Nombres de Harshad |
>>>
Nombres de Friedman |
|
833. Partitions |
|
||
|
Partitions = toutes les additions pour atteindre le nombre. La recherche des facteurs et des diviseurs d'un
nombre font partie de la théorie multiplicative
des nombres. Il existe aussi une théorie additive
qui examine la possibilité de réaliser des additions pour atteindre le
nombre. Par exemple pour 200 = 1 + 199 = 1 + 1 + 198 = 5
+ 195 … Arrêtons l'énumération car il existe presque
quatre mille milliards (3 972 999 029 388) telles additions que l'on nomme partitions du nombre. Avec ces quantités, on comprend que l'étude des
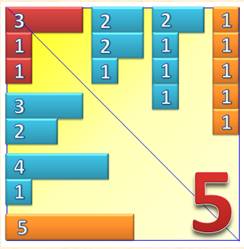
partitions soit plus complexe que celle des produits de facteurs. Plus raisonnable, le nombre 5 possède sept
partitions. Elles sont présentées de manière originale par le diagramme de Ferrers. |
Diagramme de Ferrers
Les sept
partitions du nombre 5. |
||
|
Brèves associées |
>>>
Partitions
et décompositions |
>>>
Brèves Théorie – Index |
|
|
Pour en savoir plus |
>>>
Partitions |
>>>
Diagramme de Ferrere |
|
834. Sommes particulières |
|
|||
|
Théorème de Waring Le théorème de Waring assure la partition en
carrés, cubes et autres puissances en une somme comprenant maximum fini de
termes. Théorème
Parmi les nombreuses autres partitions d'un
nombre, on retient celles qui sont notables, comme celles présentées
ci-dessous. |
Cas du nombre 200
Avec 200, il suffit de deux carrés alors que le
maximum est 4; avec la puissance 5, il en faut 14 pour un maximum de 37. |
|||
|
Somme de nombres consécutifs 200 = 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 Somme de nombres triangulaires |
Somme de nombres premiers 200 = 3 +
197 = 7 + 193 = 19 + 181 = … Somme de puissances 200
= 2² + 14² =
2² + 4² + 6² + 12² = 102 + 102 =
6² + 62 + 8² + 8²
200 = 23
+ 43 + 43 + 43 200 = 15²
– 5² = 27² – 23² = 51² – 49² 200 = 63
– 42 = 93 – 232
|
|||
|
Brèves associées |
>>>
Somme de
nombres consécutifs |
>>>
Brèves Opérations – Index |
||
|
Pour en savoir plus |
>>>
Somme des nombres entiers >>>
Nombres triangulaires |
>>>
Théoème de Waring |
||
835. Nombre glissant |
|
|||
|
Nombre glissant Nombre n
tel qu'il existe deux nombres entiers x et y tels que:
Nombres glissants jusqu'à 200
|
Le nombre 200 est un nombre
glissant
Autre exemple avec 133
|
|||
|
Brèves associées |
>>>
Nombres
narcissiques |
>>>
Brèves Types – Index |
||
|
Pour en savoir plus |
>>>
Nombres glissant |
>>>
Fractions égyptiennes |
||
836. Suite de Padovan |
|
|||
|
Suite de Padovan Suite de nombres, cousine de celle de Fibonacci
(1, 1, 2, 3, 5, 8, 13 …) – Chaque terme est la somme des deux précédents. Avec la suite de Padovan, les trois premiers
termes sont 1 et chaque nouveau terme (n + 1) est calculé à partir de
l'avant-dernier (n – 1) additionné au précédent (n – 2): |
Suite de Padovan jusqu'à 200 Nombre plastique Le rapport entre deux nombres successifs de la
suite de Fibonacci tend vers le nombre d'or, la solution positive de x² =
x + 1. Celui de la suite de Padovan tend aussi vers une
constante. Elle est solution de l'équation: x3 = x + 1 dont la
racine réelle est le nombre plastique:
1,32471… |
|||
|
Brèves associées |
>>>
Suite de
Sherlock Holmes |
>>>
Brèves Suites – Index |
||
|
Pour en savoir plus |
>>>
Suite de Fibonacci >>>
Suite de Padovan |
>>>
Nombre d'or |
||
837. Jeu des quatre 4 |
|
|||
|
Le célèbre jeu des quatre 4 (four
fours puzzle) Les amateurs d'amusements arithmétiques se sont
donné le défi de trouver des opérations qui combinent quatre nombres 4 avec
pour résultat les nombres successifs, de plus en plus grands. Ainsi, pour notre nombre: Facile ? Voyez le tableau des solutions pour les onze
premiers nombres. Oui, les solutions nécessitent un peu d'astuce. Pour le nombre 11, il faut même aller chercher la
racine carrée. Les amateurs rivalisent d'inventions, utilisant
des opérateurs moins connus pour atteindre les plus grands nombres. |
Solutions pour les nombres de 0 à
11
Solution faisant intervenir une
factorielle 19 = 4! – 4 – 4 / 4 = 24 – 4 – 1 |
|||
|
Brèves associées |
>>>
Somme de trois nombres = 30 |
>>>
Brèves Jeux – Index |
||
|
Pour en savoir plus |
>>>
Jeu du quatre 4 >>>
Chiffres en miroir |
>>>
Racine carrée >>>
Factorielle |
||
838. Jeu pannumérique |
|
|||
|
Un autre jeu non moins célèbre Ici, on demande d'utiliser les nombres de 1 à 9
dans l'ordre et d'ajouter des opérateurs classiques pour atteindre un nombre
donné On demande souvent quelle est la solution pour
100. Celle-ci, par exemple, utilise un maximum d'additions: |
Solutions pour le nombre 200 – Exemples 200 = 1 × 2 –
3 + 45 + 67 + 89 |
|||
|
Brèves associées |
>>>
Dix en
chiffres |
>>>
Brèves Jeux – Index |
||
|
Pour en savoir plus |
>>>
Faire 100 avec les 9 chiffres |
>>>
Les chiffres de l'année 2020 |
||
839. Bases de numération |
|
|||
|
Système décimal – Base 10 Nous comptons en utilisant un système de numération de position à base 10. Ce qui veut dire qu'implicitement: Un nombre comme 213 se développe en: Nous utilisons dix chiffres qui ont un poids en
multiples de 10 selon leur position. En partant de la droite, les chiffres successifs
sont à multiplier par: |
Système de numération en base 2 ou
binaire Tout en conservant le système de position, on
peut se limiter à deux chiffres: {0 et 1}. Alors 200 s'écrit: 1100 1000 dont le
développement est le suivant: Autres bases de numération (par
exemple) 200 = 404 en base 7 = 4 ×
49 + 0 x 7 + 4 200 = 88
en base 24 = 8 x 24 + 8 × 1 |
|||
|
Brèves associées |
>>>
Base 12 –
Douzaine et grosse |
>>>
Brèves Numération – Index |
||
|
Pour en savoir plus |
>>>
Système décimal |
>>>
Binaire |
||
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()