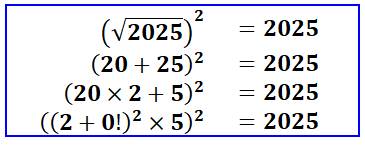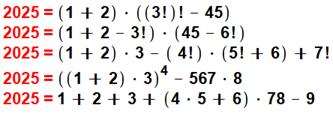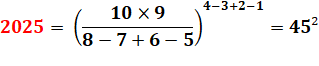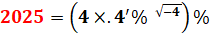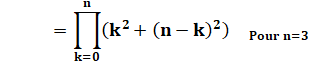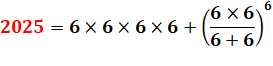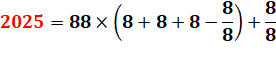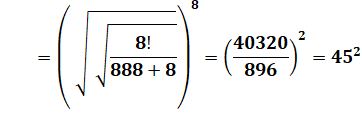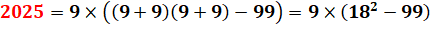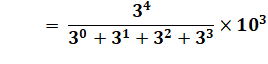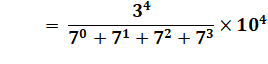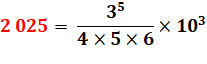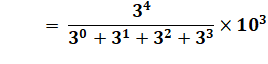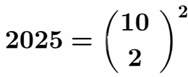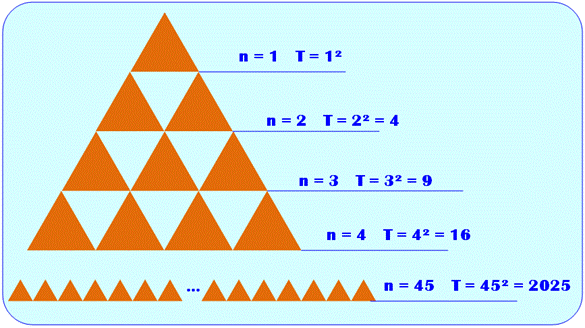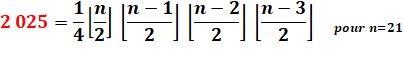|
Création du: 14/10/2024 Édition du: 11/05/2025 |
|
Dictionnaire des Nombres |
|||
|
1 / 10 / 50 / 100 / 500
/ 1000 / 1500 / 1900 / 2000 / 2016 / 2017 / 2018
/ 2019 / |
2025 |
2031 à
2099 / 3000 / 5000 / 10 000 / 20 000 / 50 000 / 100 000 / 106 / 109
/ 10100 Autres |
|
|
2020 / 2021 / 2022
/ 2023 / 2024 / 2025 / 2026 / 2027 / 2028
/ 2029 / 2030 |
|||
![]()
Index 2025 – ONZE pages pour ce nombre exceptionnel
|
Nombre 2025 |
||
|
Actualités
de 2025 |
Humour
2024-2025 |
Chiffres de
2025 (jeu) |
Faites
un double-clic pour un retour en haut de
page
|
Nombre Strobogrammatique ou ambigramme
|
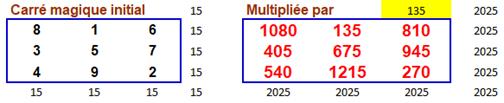
Carrés particuliers avec les chiffres de 2025
|
Motif infini
avec 2025 = 45²

Voir Pépites numériques
|
2 025 = 34 × 52 |
|
|
|
2 025 = (2 + 0!)² + 5 = ((2 + 0!)² × 5)² = (202 × 5) × 2 + 0 × 2 + 5 |
La
deuxième ligne utilise un 2 en trop. |
|
|
2 025 = 211 + 0 + 2 – 5² = 2048 –
23 |
Merci à Rachid |
|
|
2 025 = 16 × 34 × 52 × 70 2 025 = -(1+2) + (3!)4 + 5 + 6! + 7 |
|
|
|
2 025 = (2 × 22 + 1)² = 211 –
2 × 11 – 1 |
|
|
|
2 025 = (3 + 2)2 × 32 + 2 = 25 × 81 |
|
|
|
2 025 = 211 – 23
|
|
|
|
2 025 = (0²+3²)(1²+2²)(2²+1²)(3²+0²) = 9
× 5
× 5
× 9 |
|
|
|
2 025 = 205² – 200² = 5 × 405 |
||
|
Avec chiffres de 2 025
|
Exemples pour les nombres de 0 à 16. Suite >>> |
|
|
Avec chiffres de 1 à 5
|
Contribution d'Alain Zalmanski |
|
|
2 025 = 12 × 3 + (4 + 5)(6 + 7)(8 + 9) = 36 + 1989 2 025 = 9 × 8 + 76 + 54 × 3 + 2 × 1 = 72 + 76 + 625 × 3 + 2 2 025 = (–1 – 2) (3 + 4!) (5 – 6 – 7 – 8 – 9) 2 025 = –9 (8+7) + 6! × (5 + 4 – 3 – 2 – 1) |
Solutions
par Inder J. Taneja
et autres |
|
|
2 025 = (1 + 2) × 3 + 4 × 56 × (−7 + 8) × 9 2 025 = (1 × 2 + 34) × 56 + (−7 + 8) × 9 2 025 = − (1 + 2 × 3) + (34 − 5) × 67 + 89 |
|
|
|
2025 = 12 × 3 + 45 × 6 × 7 + 89 + 10 2025 = 10 + (9 + 8 × 76 + 54) × 3 + 2 × 1
|
|
|
|
2 025 = (10
+ (9 + 8 × 7) × 6) × 5 + 4 × 3 × 2 + 1 =
2000
+ 45 |
|
|
|
= (4 × (4/900) -2) / 100 = (4 × (1/225) -2) / 100 = (4
× 50625) / 100 = 202500/100 |
Avec
le symbole %
qui divise par 100 et la notation anglaise: .4’ = 0, 444... =
4/9.
Solution
par Paul Bourke |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Source "2025 puzzle" et autres
|
Ordre 3
|
|
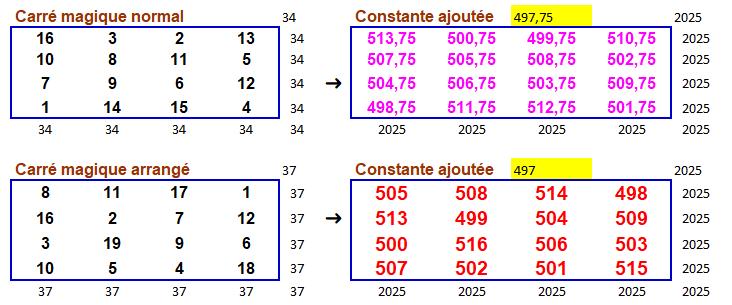
Ordre 4
|
|
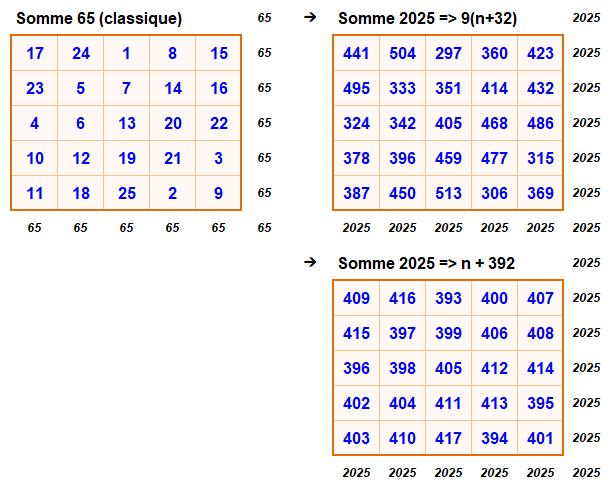
Ordre 5
|
Curiosités
|
2 025 = (0 + 3²) (1² + 2²) (2² + 1²) (3² + 0²)
|
Liste:
0, 1, 32, 2025, 204 800 … OEIS A323540 |
|
|
|
|
|
|
|
|
|
|
= 10 × 9 /
2 = 90 / 2 |
|
|
|
2 025 |
Liste:
1, 2, 3, 4, 5, 6, 7, 8, 9, 12, 13, 14, 15, 16, 17, 18, 19, 23, 24, 25, 26,
27, 28, 29, 34, 35, 36, 37, 38, 39, 45, 46, 47, 48, 49, 56, 57, 58, 59, 67,
68, 69, 78, 79, 89, 102 … 8659, 8669, 8679, 8689, 8709, 8719, 8729, 8739, 8749,
8759, 8769, 8779, 8789, 8809, 8819, 8829, 8839, 8849, 8859, 8869, 8879, 8889. Ils sont seulement 255
avec des chiffres tous plus grands les uns que les autres. Liste:
1, 2 … 89, 123, 124, 125, 126, 127, 128, 129, 134 …2689, 2789, 3456, 3457,
3458, 3459, 3467, 3468, 3469, 3478, 3479, 3489, 3567, 3568, 3569, 3578, 3579,
3589, 3678, 3679, 3689, 3789, 4567, 4568, 4569, 4578, 4579, 4589, 4678, 4679,
4689, 4789, 5678, 5679, 5689, 5789, 6789. Voir Nombre 285 |
|
|
2 025 |
|
|
|
2 025 |
= 45 ×
45 = 2025 |
|
2 025 |
La quantité de triangles, pointe en haut et
pointe en bas, sur une ligne est égale au nombre impair suivant la quantité
de la ligne du dessus. Or, la somme des nombres impairs est
un carré. |
|
2025 |
|
|
|
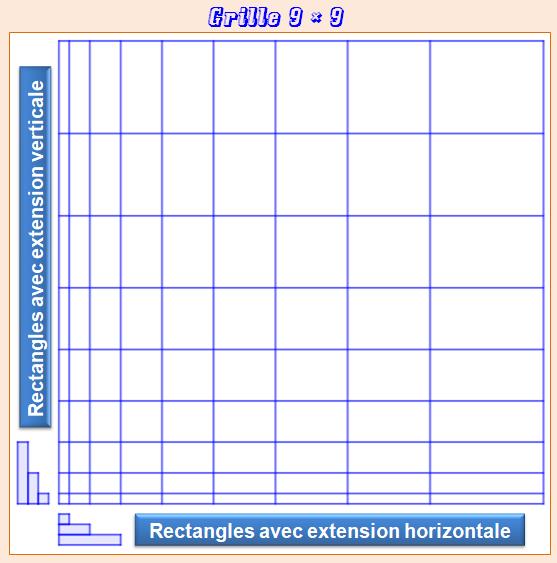
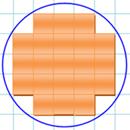
2 025 |
À
titre d'exemple, l'illustration montre le cas simple de 21 carrés unités
contenus dans un cercle de rayon égal à 3 unités. Résoudre
le cas général pour un rayon R donné est connu comme le problème de
Gauss. |
|
|
2 025 |
Liste:
1, 3, 15, 133, 2025, 37851, 1030367, 36362925, 1606008513, 87656896891,
5778121715415, 452794797220965, 41609568918940625, … A006717 |
|
|
|
|
|
Autour
du nombre
|
122333444455555
… 454545 => 2 025 chiffres |
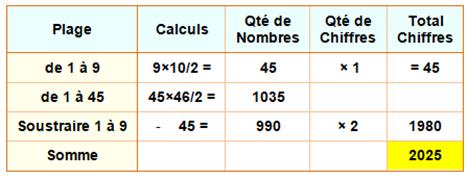
Calculs
|
|
|
|
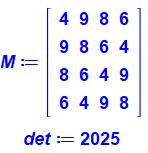
Ces nombres (4, 6, 8, 9) en permutations
circulaires sont les quatre nombres composés inférieurs à 10. Voir Calcul pas à pas de ce
déterminant
Source:
Aplenty number 2025 |
|
|
(12025
+ 22025 + 32025 + 42025 + 52025 |
|
|
SUITE SUR LE
NOMBRE 2025 voir index en Haut de page (ou double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Sites |
|
|
Cette page |
![]()