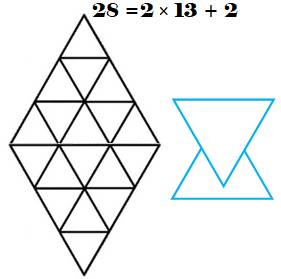|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Compter les triangles Il existe plusieurs méthodes pour faire un décompte
systématique. Quelques exemples. |
|
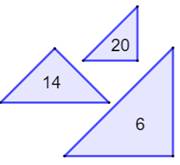
Combien
de triangles dans cette figure ?
|
|
|
||
|
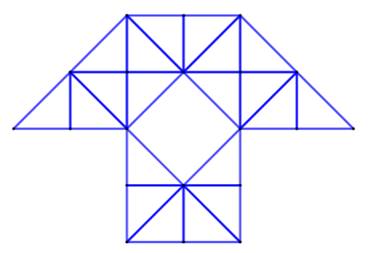
Combien
de triangles dans cette figure ? Ils sont
de trois tailles et le décompte est le suivant:
|
40 triangles sur cette figure
|
|
|
|
||
|
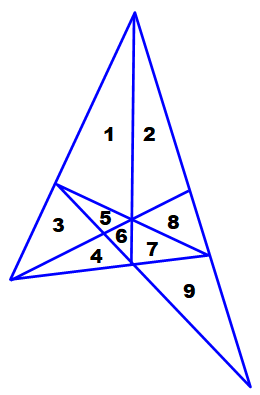
L'approche
consiste à compter les triangles seuls ou assemblés:
Total: 9
+ 5 + 6 + 5 + 2 + 0 + 1 + 1 = 29 |
|
|
Voir Brève
854
|
|
||
|
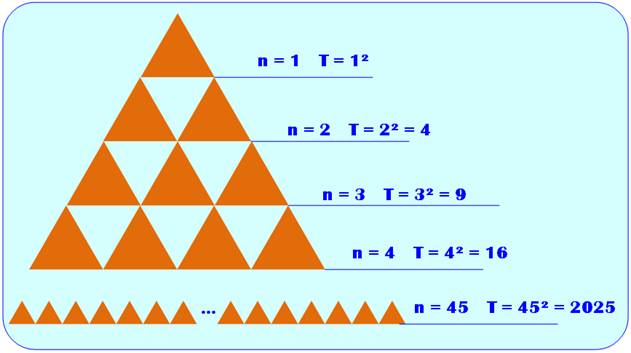
Quantité de triangles
équilatéraux ÉLÉMENTAIRES dans un triangle équilatéral T = n² (n est le côté du triangle)
Suite en Compter les triangles
équilatéraux élémentaire |
||
|
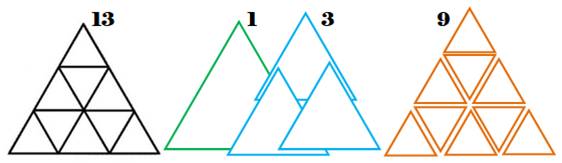
Quantité de TOTALE de
triangles équilatéraux dans un triangle équilatéral
Cette figure de
gauche comporte 13 triangles équilatéraux. Dont 1 grand
(vert) et 9 petits (bruns) faciles à dénombrer. Plus 3 moyens (bleus)
à ne pas oublier. Suite en Compter tous les triangles
équilatéraux |
||
|
En dupliquant
cette figure (losange),
on double la quantité de triangles et on ajoute deux triangles moyens
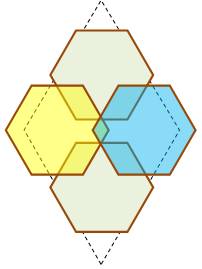
(bleus), à cheval sur les deux figures initiales. La première
figure montre un hexagone inscrit
dans le triangle équilatéral. La seconde montre deux fois cet hexagone (vert
clair) plus deux supplémentaires (jaune et bleu) à cheval sur les deux
figures initiales. |
|
|
|
|
|
|
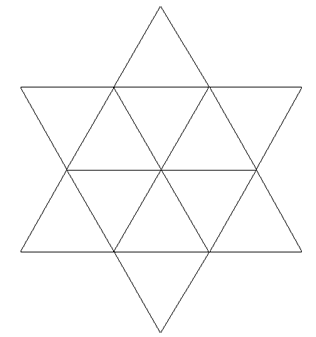
Quelle est la
quantité de triangles dans cette figure en étoile à six branches ?
20 = 12 petits (6
au centre et 6 pour les branches) + 6 moyens + 2 grands |
|
|
|
||
|
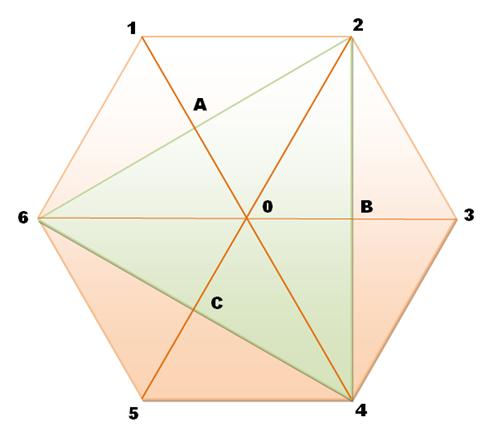
Quelle est la
quantité de triangles dans cet hexagone
régulier? Notez que toutes
les diagonales ne sont pas présentes. Pour l'hexagone avec toutes es
diagonales >>>
Les compter
visuellement ne vous rendra pas confiant du résultat (sauf si vous le
connaissez par avance!) La méthode sûre
consiste à prendre chaque côté possible et à chercher à former un triangle
avec les autres points. On procède par numéros croissants: un triangle 123
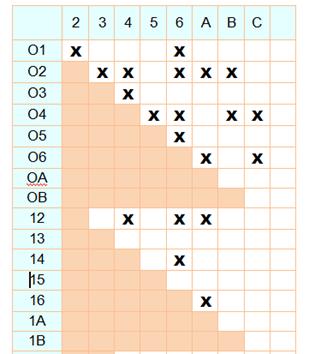
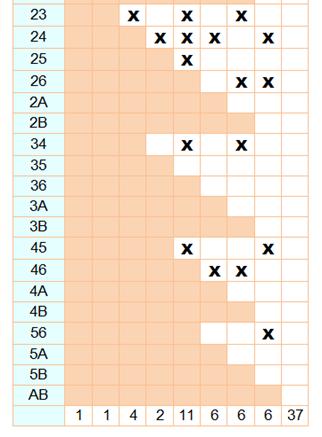
est le même que le triangle 231, par exemple. Un tableau fera
l'affaire. |
||
|
Le décompte donne 37 triangles dans cette figure. |
|
|
|
|
|
|
Quelle est la
quantité de triangles dans cette figure
triangulaire?
Il
y en a 47 Voyons comment
les dénombrer sûrement: |
|
|
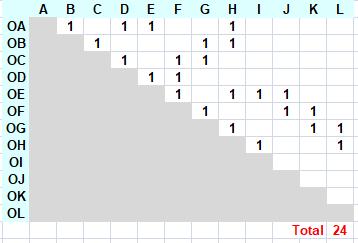
Décompte selon méthode
logique:
|
|
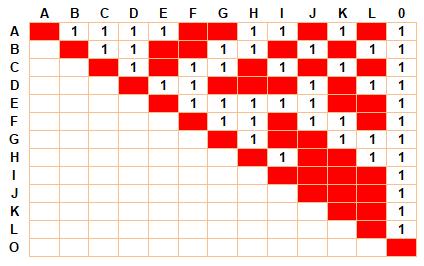
Décompte exhaustif
Exemples ABC, ABD, ABF, ABG, ACE, etc. Toutes les possibilités: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
14 |
10 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
7 |
9 |
5 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
0 |
0 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
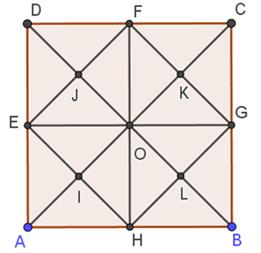
Combien
de triangles ?
|
Dénombrement Par la méthode directe Bilan 4 + 4+4 + 4x4 + 4x4 = 11 x 4 = 44
triangles |
|
||||
|
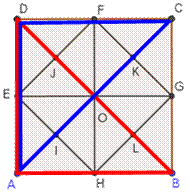
Les 4 triangles formés par les diagonales d'un carré. |
Les 4 triangles rouges et les 4 triangles bleus. |
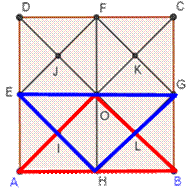
Quatre fois les 4 triangles avec les diagonales d'un
carré. |
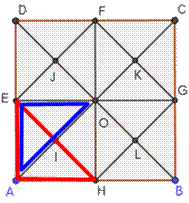
Quatre fois les 4 petits triangles dans un carré. |
|||
|
Méthode de la (Suivre
le lien pour exemple d'application) |
|
|||||
|
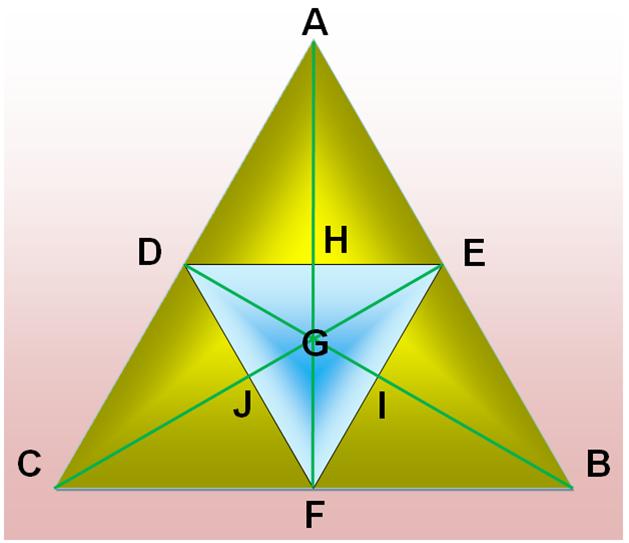
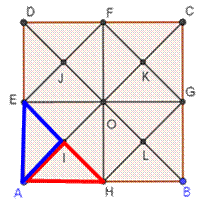
Méthode pas à pas Lecture sur le
graphique en procédant par ordre alphabétique.
|
Sans le O central ABC, ABD, ACD, AEH, AEI, AHI, BCD, BGH, BGL, BHL CFG, CFK, CGK, DEF, DEJ, DFJ, EFG, EFH, EGH, FGH, Total 20 Avec le O central
|
|||||
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Triangle/Particul/TrgTrg.htm |
![]()