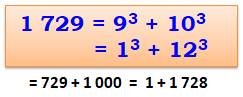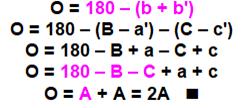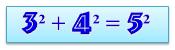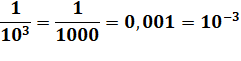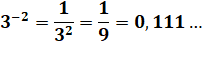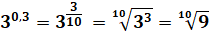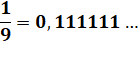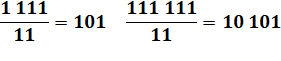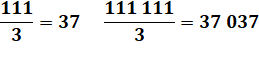|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
BRÈVES de MATHS – Page 3 Un millier de faits et chiffres sur les nombres et les
mathématiques
En principe ces pages sont très abordables sans
connaissances particulières de maths. Elles sont proposées dans un ordre
quelconque favorisant la découverte de sujets multiples. |
Anglais: Facts and figures about numbers and mathematics
40. Nombre 1729 – Taxicab |
|
|||
|
Vers 1915, Hardy rend visite
à Ramanujan hospitalisé. – Ça va t'amuser, j'ai retenu le numéro de mon taxi:
1729. Le mathématicien prodige indien lui répond instantanément: - Tu sais,
ce nombre n'est pas quelconque. C'est le seul nombre qui peut être exprimé
comme la somme de cubes de deux paires différentes de nombres. Taxicab n°2
|
Nombres taxicab Depuis les plus petits nombres, somme
plusieurs fois de deux cubes, sont nommés nombres taxicab. Avec deux fois, on trouve 1 729; et,
avec trois fois la somme, le plus petit nombre est déjà dans la dizaine de
millions: Taxicab n°3
Belle relation 63 + 83 + 103 = 123 216 + 512 +
1000 = 1 728 |
|||
|
Pour en savoir plus |
>>>
Cubes >>>
Somme de cubes >>>
Nombres Taxicab >>>
Pépites numériques |
>>>
Somme des nombres successifs au cube >>>
Ramanujan >>>
Hardy >>>
Nombre 1 729 |
||
41. Parenthèses – (a+b)(c+d) |
|
|||
|
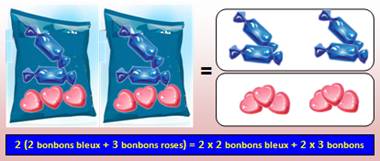
Analogie avec un paquet de bonbons Voyez cette équivalence: d'un côté 2
paquets de bonbons chacun contenant 2 bonbons bleus et 3 roses. De l'autre, la
même quantité sous la forme de 2 fois 2 bonbons bleus et 2 fois 3 bonbons
roses.
(ajouter: roses en fin de
ligne) On écrit en abrégé: 2 (2B + 3R) = 2 x 2B + 2 x 3R =
4B + 6R Et d'une manière générale: a (c + d) = a.c + a.d |
Double dépliement de (a + b)(c + d) Quel est l'élève qui n'a pas buté sur
le développement de cette expression? Avec ce que nous venons de voir (à
gauche), la solution va vous sembler facile (même si l'analogie avec les paquets de bonbons
s'arrête là). On fait néanmoins un paquet avec (a +
b) que l'on nomme P. Alors: (a +
b) (c + d) = P (c + d) Nous sommes revenus au cas que nous
connaissons, alors développons: P (c + d) = P.c + P.d Deuxième étape, on remplace P par sa
valeur: (a +
b) c + (a + b) d Sur notre lancée, nous poursuivons le
développement: (a + b) c + (a + b) d
= a.c + b.c + a.d + b.d Nous tenons le développement complet
de notre expression: (a + b) (c + d) = a.c + b.c + a.d + b.d |
|||
|
Brèves associées |
>>>
Multiplications et parenthèses |
|||
|
Pour en savoir plus |
>>>
Bases du calcul algébrique >>>
Calcul avec parenthèses |
>>>
Trucs de maths – Ce qu'il faut savoir au collège, comment déjouer les pièges |
||
42. Nombres 0 et 1 – Binaire |
|
|||
|
Système décimal (10) C'est la
manière de compter des humains. 2345 = 2
x 1000 + 3 x 100 + 4 x10 + 5 On note
plutôt: 2345 = 2
x 103 + 3 x 102 + 4 x101 + 5 Le petit chiffre indique combien
de fois on multiplie par 10 Système binaire (2) C'est la
manière de compter des ordinateurs. Notre 10 (quantité de chiffres en
décimal) est remplacé par 2 (quantité de chiffres en binaire). Exemple 1101 = 1
x 23 + 1 x 22 + 0 x 21 + 1 Si on calcule la somme: 8 + 4 + 0 + 1 = 13. 1101 en
binaire est égal à 13 en décimal. |
Les ordinateurs comptent à leur
manière Les ordinateurs ne reconnaissent que la présence
d'un courant électrique (codé par 1) ou l'absence de courant (codé par 0). Ils comptent avec seulement ces deux chiffres: 0
et 1.
Compter en binaire et additionner en binaire |
|||
|
Pour en savoir plus |
>>>
Décimal >>>
Binaire |
>>>
Nombre 0 >>>
Nombre 1 |
||
43. Périmètre et Aire |
|
|||
|
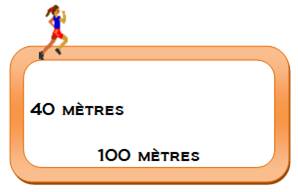
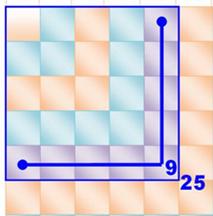
Faire le tour En faisant le tour du stade, ce coureur aura
parcouru: 100 + 40 + 100 + 40 = 280 mètres Deux fois la longueur plus deux fois la largueur.
Périmètre Un mot
facile à retenir en le comparant au mot périphérique, ces voies rapides qui
font le tour de la ville.
|
Carreleur Avant la pose, le carreleur prévoit les achats: 15 rangées de 30 carreaux, soit 450 carreaux pour
couvrir toute la surface.
Aire ou surface On
préfère le mot "aire" lorsqu'il s'agit de la mesure d'une surface. On
définit la surface d'un corps, on en calcule son aire. Le mot
"aire" vient du latin area (surface, superficie) que les anglais on
adopté tel quel. |
|||
|
Pour en savoir plus |
>>>
Périmètre >>>
Périmètre – Curiosités >>>
Mon petit formulaire |
>>>
Aire >>>
Origine des mots |
||
44. Fractales |
|
|||
|
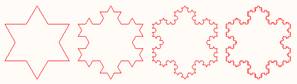
Le flocon de neige – Fractale de
Koch
En commençant avec l'étoile de gauche, sur chaque
segment on implante un triangle sans base. On recommence … La forme
festonnées obtenue est une ligne fractale. Sa dimension n'est pas entière!
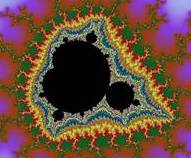
Elle vaut 1, 26… à mi-chemin entre une courbe et une surface. Itération sur le plan L'idée ici est d'observer le comportement d'une
fonction simple (x² + a) en un point du plan. La fonction prend rapidement de
grandes valeurs, alors le point est peint en blanc, sinon il est matérialisé
en noir. Ce résultat simple appliqué à tous le plan
produit la figure du "pou". Elle es très facile à programmer même
avec un logiciel abordable par tous comme Scratch. |
Figure fractale dite du
"pou" et zoom
En zoomant sur cette figure,
on retrouve inlassablement cette même figure du "pou" parmi des
formes de grande beauté (comme celle montrée à droite). Il existe de nombreuses
figures fractales dans la nature (ligne de côte ou encore la rose des sables) Éponge de Menger
Magnifique exemple de
fractale en relief (3D). Sa dimension fractale est égale à 2,72… Pas un vrai
volume (dimension 3), ni bien sûr une surface (dimension 2) |
|||
|
Pour en savoir plus |
>>>
Fractales >>>
Nombres 4,699… |
>>>
Constante de Feigenbaum >>>
Programmation fractale avec Scratch |
||
45. Nombre 1,61818… & ≈ nombre d'or |
|
|||
|
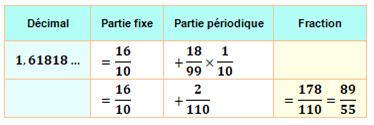
Fraction approximant le nombre d'or
(Phi)
Nombre décimal périodique Le nombre 89/55 = 1,6181818 … est un nombre
comprenant une partie entière (1) et une partie décimale (6181818…). Il est vu aussi comme ayant une partie fixe (1,6)
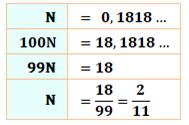
et une période (18). Amusants! 9/99 =
0,090909… 19/99 = 0,191919… 55/99 = 0,555555… 70/99 = 0,707070… 98/99 = 0,989898… |
Conversion d'un nombre purement
périodique
En multipliant par 100, on
isole une partie entière égale à la période. La soustraction élimine la
partie décimale. Reste à effectuer la division et à simplifier la fraction. Conversion d'un nombre avec partie
fixe
La conversion s'applique
successivement à la partie fixe puis à la partie périodique. |
|||
|
Pour en savoir plus |
>>>
Nombre d'or >>>
Nombre 99 >>>
Nombre 1,61818… |
>>>
Fractions >>>
Nombres périodiques >>>
Conversion décimal / fraction |
||
46.
Infini -
|
|
|||
|
Infini paradoxal Nombres entiers: 1, 2, 3, 4 … Nombre impairs: 1, 3, 5, 7 … Nombres pairs: 2, 4, 6, 8 … Nombres au carré: 1, 4, 9, 16 … Vous
conviendrez que chacune de ces énumérations ne s'arrêtent jamais. On dit
qu'il y a une quantité infinie de nombres entiers. Mais,
c'est vrai aussi pour bien d'autres. Et c'est toujours le même infini? Ben,
oui!
Nombres réels et nombres entiers L'infini des nombres entiers est "moins
riche " que l'infini de la quantité de points sur une
droite. |
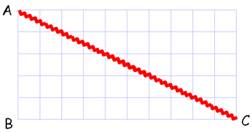
Infini infiniment paradoxal
Le segment AC est l'hypoténuse d'un triangle
rectangle. Sa longueur se calcule avec le théorème de Pythagore: AC² = AB² + BC² = 5² + 10² = 125 AC = 11,18 unités Imaginons AC comme les marches d'un escalier.
Chaque marche horizontale se projette sur BC; alors la longueur de toutes ces
marches est égale à BC. De même pour les faces verticales des marches qui se
projettent sur AB; alors leur longueur totale est égale à AB. En résumé: la longueur de l'escalier est égale à
AB + BC = 5 + 10 = 15, et cela quelle que soit la taille des marches, même
extrêmement petites. Paradoxe: AC = 11,18 ou AC = 15 unités? Solution: l'infini continu (segment) est différent
de l'infini discret (marches). Conclusion: Il existe plusieurs sortes
d'infinis. |
|||
|
Pour en savoir plus |
>>>
Infini >>>
Nombres entiers >>>
Nombres réels |
>>>
Triplets de Pythagore >>>
Diagonale de Cantor >>>
Hypothèse du continu |
||
47. Démonstration en géométrie |
|
||||
|
Démonstration en géométrie Une démonstration est un raisonnement rigoureux qui, à partir de données
(les hypothèses) aboutit à des conclusions (ce qu'il faut démontrer – CQFD)
et, cela en appliquant des théorèmes (propriétés) connus, car déjà démontrés. En remontant à la source des théorèmes, on trouve les axiomes, comme
ceux d'Euclide: des propriétés que l'on pose comme évidentes, indémontrables. Exemple de démonstration |
|
||||
|
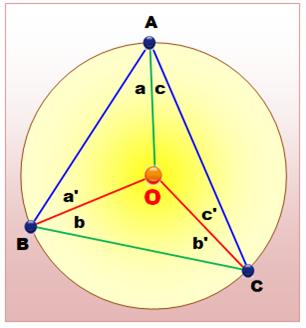
Hypothèses
Ce qu'il faut démonter Montrer que la mesure de l'angle O vaut deux fois
celle de l'angle A. Théorèmes utilisés 1.
Dans tout triangle, la somme des angles vaut 180° 2.
Un triangle ayant deux côtés égaux est un triangle isocèle. 3.
Dans un triangle isocèle les angles opposés au sommet sont égaux. |
Raisonnement Les segments OA, OB et OC sont des rayons du
cercle: ils ont même longueur. Les triangles AOB, AOC et BOC ayant deux côtés de
même longueur sont isocèles. Leurs angles, deux à deux, sont égaux. En termes
d'angles, on a: a = a' ; b = b'
; c = c' En évaluant l'angle O et
appliquant le théorème 1, plusieus fois.
Le carré noir indique que la démonstration est
terminée. |
||||
|
Pour en savoir plus |
>>>
Bases de la géométrie >>>
Triangle isocèle >>>
Angles dans le cercle (présentation complète de cette démonstration) |
>>>
Démonstrations – Types >>>
Les axiomes d'Euclide |
|||
48. Nombres carrés |
|
|||
|
Carré et carré Très tôt dans notre scolarité nous savons
calculer la surface d'un carré ou d'un rectangle. Aire du carré: ABCD = c x c = c2
Sur le terrain Nous savons que la superficie d'un terrain se
compte en mètres carrés et on écrit m². Le petit 2 en exposant signifie ce
nombre est le produit de deux mesures en mètres. Les premiers carrés 1, 4, 9, 16, 25,
36, 49, 64, 81, 100 … |
Nombres carrés Si l'on s'intéresse à une bordure en équerre du
carré, on trouve une nombre impair (9). Le carré est finalement la somme de
tous ces nombres impairs successifs: 1 + 3 + 5 + 7 + 9 = 25 = 5².
Écart entre carrés successifs 5² = 25 et 25 + 5 + 6 = 36 = 6² Pour passer au carré suivant, il suffit d'ajouter
le nombre et son suivant. Aubaine pour le calcul mental. (n + 1)2
– n2 = n + (n + 1) |
|||
|
Pour en savoir plus |
>>>
Nombres carrés >>>
Calcul des carrés sur les doigts |
>>>
Carré en géométrie |
||
49. Pythagore de Samos (580-495 av. J.-C.) |
|
|||
|
Il est né à Samos, sur une
île à l'ouest de la Turquie actuelle |
Philosophe grec
à l'origine d'importants développements en mathématique, astronomie et
musique. Il entreprend des voyages d'étude qui le mènent en Perse, en Gaule,
en Crète, en Égypte. Fondateur de
l'école philosophique et religieuse à Crotone (Italie du sud) qui pratiquait
le secret en externe et le partage des connaissances en interne. Pythagore mourra
lors de l'incendie de l'École. Connu des
collégiens pour son fameux théorème qui lie les mesures des côtés d'un
triangle rectangle. Il fut le premier à l'avoir démontré. Il était connu des
Babyloniens mille ans auparavant. Suite à leurs
observations, et même leurs émerveillements en mathématique, en astronomie et
en musique, Pythagore et ses adeptes pensaient que le monde était décrit par
les nombres entiers. La diagonale du carré ne rentrait pas dans ce paradigme
et cela jeta un trouble. En effet, avec un carré de côté unité, la diagonale
mesure racine carré de 2, un nombre incommensurable (une infinité de chiffres
différents derrière le virgule, donc un nombre irrationnel). En astronomie,
les pythagoriciens sont les premiers à considérer la Terre comme une sphère
en révolution, avec d'autres planètes, autour d'un feu central. |
|||
|
Brèves liées |
>>> Les
grands savants de l'Antiquité – B17 >>>
Triplets de Pythagore – B25 |
|||
|
Pour en savoir plus |
>>>
Pythagore >>>
Contemporains >>>
Nombres entiers >>>
Nombres irrationnels |
>>>
Racine de 2 >>>
Triangle rectangle >>>
Théorème de Pythagore >>>
Triplets de Pythagore |
||
50. Suite miroir |
|
|||
|
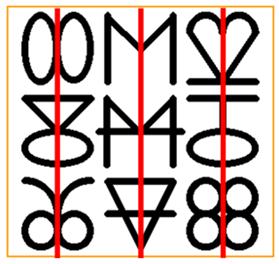
Énigme Que cache cette
séquence? Sauriez-vous deviner la suite?
|
Solution Couper chaque
figure en deux par un trait vertical. La symétrie
révèle les chiffres successifs.
|
|||
|
Avant 1970, ce puzzle n'était pas très connu et, il était présenté à
des personnes de divers niveaux d'éducation. En général, le taux de réussite
était plus grand avec les élèves de l'école primaire qu'auprès de ceux des
grandes écoles. |
||||
|
Pour en savoir plus |
>>>
Séquence miroir |
>>>
Énigmes classiques >>>
Jeux et énigmes |
||
51. Carré magique 5x5 |
|
|||
|
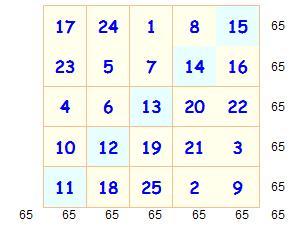
Un carré magique est une grille de chiffres telle que la somme
des nombres sur les lignes, les colonnes et les diagonales sont identiques. La constante magique est égale à la somme de tous les nombres de 1 à 25
divisée par 5 = ½ (25 x 26) / 5 = 65. La construction est très simple:
|
Carré magique 5x5
La somme des extrémités des "diagonales" est égale à 26. Il existe plusieurs millions de tels carrés magiques 5x5. |
|||
|
Brèves associées |
>>> Carré
magique 3x3 |
|||
|
Pour en savoir plus |
>>> Carré magique 5x5 >>>
Carré latins >>>
Somme des entiers successifs |
>>>
Carré magiques de toutes sortes >>>
Sudoku >>> Constante magique |
||
52. Nombre 3 – TROIS |
|
|||
|
Propriétés Le nombre 2 est un nombre impair, Tous les nombres premiers à partir de 3 sont
impairs. En romain 3 devient III et en binaire 3 s'écrit
11, car 3 = 21 + 20. C'est un nombre triangulaire:
Divisibilité Un nombre est divisible par 3 si la somme de ses
chiffres l'est. Un nombre diminué de la somme de ses chiffres est divisible
par 3: Le produit de trois nombres consécutifs est
divisible par 3. Symbole Le nombre 3 est souvent associé au divin: trinité
des chrétiens, la triade juive, Trimurti chez les Hindous, les trois
véhicules bouddhiques, etc. |
Carrés Le nombre 3 au carré est le premier terme du
célèbre triplet de Pythagore:
Géométrie
Une figure à trois côtés est un triangle. Un point de l'espace est défini par trois
coordonnées. L'espace à trois dimensions (3D). Amusements
Trois petits tours et puis s'en vont. Jamais deux sans trois. Trèfle vient de trifolium, trois feuilles. Les trois petits cochons. |
|||
|
Brèves associées |
>>> Nombre
2 |
>>> Nombre
4 |
||
|
Pour en savoir plus |
>>>
Nombre 3 – Culture >>>
Nombre 3 – Maths >>>
Nombre 3 - Quantité |
>>>
Triangle >>>
Triplet de Pythagore |
||
53. Divisibilité des carrés et des cubes |
|
|||
|
Quel est
de degré de divisibilité du carré ou du cube d'un nombre? On
distingue le cas des nombres pairs qui sont de la forme (2k) et le cas
des nombres impairs (2k + 1). |
||||
|
PAIR (2k) |
IMPAIR (2k + 1) |
|||
|
Un nombre
pair au carré: (2k)² = 4k² Un nombre pair au carré est divisible par 4. Exemples 10² = 100
= 4 x 25 12² = 144
= 4 x 36 |
Un nombre
impair au carré: (2k + 1)² = 4k² + 4k + 1 = 4 k (k+1) + 1 Un nombre impair au carré, diminué de 1, est divisible par 8. Exemples 11² – 1 =
120 = 8 x 15 13² – 1 =
168 = 8 x 21 |
|||
|
Un nombre
pair au cube (2k)3 = 8k3 Un nombre pair au cube est divisible par 8. Exemples 43
= 64 = 8 x 8 63
= 216 = 8 x 27 |
Un nombre
pair au cube (2k + 1)3 = 8k3 +12k2
+6k + 1 = 2H + 1 Un nombre impair au cube est impair. Exemples 53
= 125 73
= 343 |
|||
|
Un nombre
pair à la puissance k est
divisible par 2k. |
Un nombre
impair à la puissance k est
impair. |
|||
|
Brèves associées |
>>>
Nombres pairs et impairs |
|||
|
Pour en savoir plus |
>>>
Carrés >>>
Cubes |
>>>
Divisibilité des carrés >>>
Divisibilité |
||
54. PUISSANCES |
|
|||
|
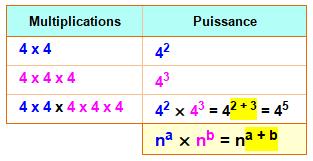
Multiplication et Puissance Tout comme la multiplication est une forme abrégée pour noter une
série d'additions, la puissance est une forme abrégée pour noter les
multiplications multiples. 4 + 4 + 4 + 4 + 4 = 5 x 4 4 x 4 x 4 x 4 x 4 = 45 On lit 4 à la puissance 5. Le nombre 5 est l'exposant. On peut aussi
noter: 4^5. Intérêt des puissances Propriété qui découle directement de la
définition
Pour multiplier deux puissances d'un même nombre, on ajoute les
exposants. Pratique, non ? Puissances 0 et 1 a0 =
1 & a1 = a |
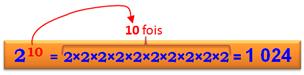
Puissance de 2
Puissance de 10
Puissances négatives
Une puissance négative est l'inverse d'une puissance.
Puissances fractionnaires
|
|||
|
Brèves associées |
>>>
Puissance de 2 et échiquier |
|||
|
Pour en savoir plus |
>>>
Puissances (normales, négatives, fractionnaires …) |
>>>
Puissances de 2 >>>
Puissances de 10 |
||
55. Arithmétique |
|
|||
|
Définition Branche des mathématiques qui considère les
propriétés des nombres pour compter (dénombrer) et calculer. Études
Étymologie Du grec arithmetike: de arithmos, nombre, et techne, qui est relatif à un art
ou à une compétence. Synonymes
Anglais Arithmetic is a branch of mathematics that deals with properties of the counting
numbers and fractions and the basic operations applied to these numbers. Amusement L'arithmétique, c'est être capable de compter
jusqu'à vingt sans enlever ses chaussures. Walt Disney |
Questions (exemples)
Techniques
Extension L'arithmétique est la science des nombres au sens
large. Aujourd'hui, elle s'étend aux
nombres réels et à des opérations avancées comme l'exponentiation. L'arithmétique modulaire s'intéresse aux restes
de la division par un nombre donné. |
|||
|
Brèves liées |
>>>
Arithmétique modulaire |
>>> Calcul
et maths |
||
|
Pour en savoir plus |
>>>
Arithmétique >>>
Les quatre opérations |
>>>
Nombres >>>
Nombres entiers |
||
56. Jeu de dés (Anglais: dice game) |
|
|||
|
Le dé à jouer
Deux faces opposées totalisent 7. Chance d'obtenir un 6 Si le dé n'est pas pipé, on a la même chance (la
même probabilité) d'obtenir chacun des
nombres de 1 à 6. À la longue, sur des milliers de lancés (disons
6000), on devrait avoir la même quantité pour chacun des chiffres: mille fois
le 1, mille fois le 2 ... mille fois le 6. On a donc; 1000 fois le 6 pour 6000 lancés. On
dit qu'on a une probabilité de 1000 sur 6000 d'avoir le 6; et, en simplifiant
la fraction: une probabilité de un sur six. Ou, en calculant un pourcentage:
16,66% Probabilité C'est une fraction dont le numérateur est la
quantité de coups favorables et le dénominateur
la totalité des coups. Cela, à condition de compter un très grand nombre
d'événements. Au dé, on a une chance sur six d'avoir un 6, mais
en lançant le dé six fois, il n'est pas certain d'obtenir un 6. On peut même
obtenir six fois le 1 d'affilé. Curiosité Avec deux dés, la probabilité d'avoir une somme
égale à 7 est de 1/6. Il y a, en effet, six possibilités de faire la somme 7:
(1+6), (2+5),
(3+4), (4+3), (5+2) et (6+1). |
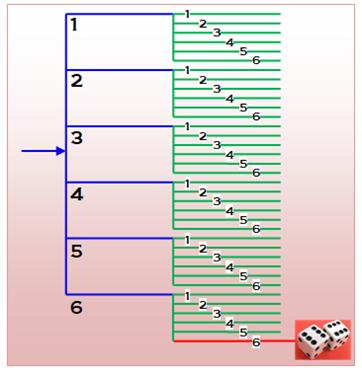
Avec deux dés Comment calculer la probabilité d'avoir un double
6? Imaginons une route pour aller d'ici au double 6. Alors, il a un choix parmi six routes au départ,
numérotées de 1 à 6. Avec le premier dé, nous nous engageons sur la route
indiquée par le numéro tiré. En bout de ce premier tronçon, le lancé du second
dé nous indique quelle est la route suivante à emprunter.
Il y a finalement 35 façons de se fourvoyer
contre une seule façon d'arriver au double 6. La probabilité du double six au lancé de deux dés
est égale à 1/36.
|
|||
|
Pour en savoir plus |
>>>
Jeu de dé >>>
Jeux et énigmes – Index |
>>>
Dénombrement >>>
Probabilités |
||
57. Nombres uniformes –Repunit |
|
|||
|
Repunit Les nombres uniformes sont formés avec un seul
chiffre. Avec le chiffre 1, on les nomme aussi repunit (répétition de l'unité, un mot-valise). Ce sont: 11, 111, 1111 … Curiosité: pyramide en 1
Curiosités: cubes 113 = 1331 et 1+3+3+1 = 8 = 23 1113 = 1 367 631 et 1+3+…+1 = 27 = 33 |
Nombre en 1 et nombre en 9
Divisibilité Tout repunit dont la quantité de chiffres est
divisible par 2 est divisible par 11.
Tout repunit dont la quantité de chiffres est
divisible par 3 est divisible par 3.
Repdigits premiers On n'en connait que cinq:
L'indice
indique la quantité de 1. |
|||
|
Pour en savoir plus |
>>>
Repunit >>>
Divisibilité |
>>>
Nombre premier >>>
Mot-valise |
||
58. Division – Exemple: 654 / 5 |
|
|||
|
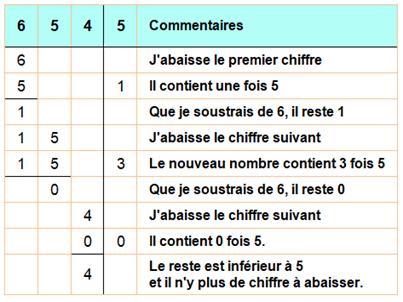
La division euclidienne consiste à effectuer la division sur
le nombre entier (sans virgule). La division est notée aussi
bien: |
||||
|
Division euclidienne On
effectue la division jusqu'à obtenir un reste inférieur au diviseur (ici 5). Lorsqu'on abaisse le dernier
chiffre 4, on effectue la dernière opération et on s'arrête. Le reste (ici 4)
est le reste final à annoncer. Résultat 654 = 5 x 130
+ 4 Je vérifie le résultat pour
vérifier l'ordre de grandeur; notamment pour confirmer la présence du 0 dans
130. 3 x 130 +
4 = 650 + 4 = 654. |
|
|||
|
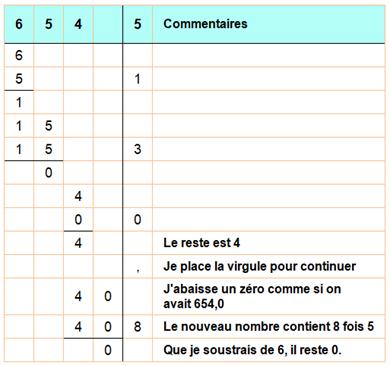
Si le reste n'est pas nul, la
division décimale consiste à poursuivre la
division euclidienne en ajoutant une virgule au nombre à diviser et des zéros
derrière la virgule. On continue la division normalement jusqu'à obtenir un
reste nul ou des chiffres qui se répètent au quotient, ou, tout simplement,
on a une quantité de chiffres suffisant. |
||||
|
Division décimale Elle
consiste à imaginer que 654 est suivi d'une virgule et de zéros; ce qui ne
change pas la valeur: 654 = 654,000 On poursuit normalement la
division après avoir placé une virgule également dans le diviseur. Ici une
seule opération supplémentaire suffit pour obtenir un reste nul. Résultat 654 = 130,8 x 5 Je vérifie le résultat: 130,8 x 5 = 654. |
|
|||
|
Pour en savoir plus |
>>>
Division euclidienne >>>
Division décimale |
>>>
Nombres entiers >>>
Nombres décimaux |
||
59. Triangles |
|
||||
|
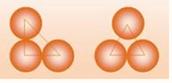
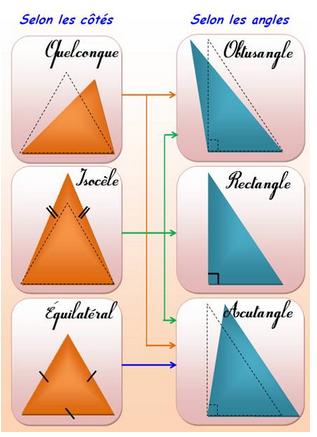
Définitions Ligne brisée fermée à trois segments. Polygone à trois côtés. Figure géométrique à trois angles (étymologie). Quatre types principaux de
triangles
|
Types de triangles
Les flèches indiquent les combinaisons possibles.
Le triangle isocèle peut être aussi bien obtusangle, rectangle ou acutangle. |
||||
|
Autres types
|
|
||||
|
Angles La somme des trois angles est égale à 180°. Chacun des angles du triangle équilatéral vaut
60°. Plan Les trois sommets du triangle définissent un
plan. Les côtés délimitent un intérieur et un extérieur. Notation: le triangle
ABC est noté: |
|||||
|
Brèves associées |
>>>
Triangle rectangle |
>>>
Droites dans le triangle |
|||
|
Pour en savoir plus |
>>>
Types de triangles |
>>>
Somme des angles dans le triangle |
|||
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()