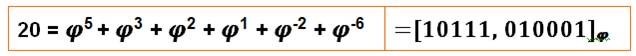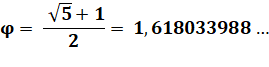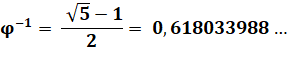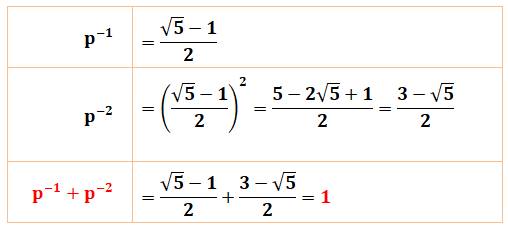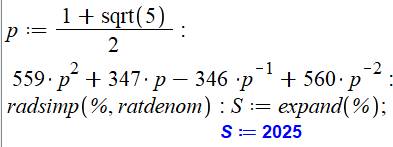Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 07/01/2025 M'écrire Brèves de Maths

INDEX Suite de Fibonacci et nombre d'or Défis en géométrie Géométrie	Nombre d'or
	Index	Valeurs	Trigonométrie	Puissances
	Tout PHI en bref	Proportion	Cercle	Fraction continue
	Débutant	Géométrie	Carré + Cercles	Numération dorée
	Introduction	Construction	Étoile	Phi et nombre 5
	Formules	Construction dorée	Ellipse	Phi et Fibonacci
	Historique	Triangle de Kepler	Aire Phi

Faites un double-clic pour un retour en haut de page

Numération dorée Expression des nombres avec le nombre d'or pour base Nous comptons habituellement en base 10. On peut aussi compter en base 2 (binaire) ou 8 ou n'importe quel nombre. Il est aussi possible de compter en base Phi, le nombre d'or. Exemple (notez la présence de puissances négatives)
	Sommaire de cette page >>> Approche >>> Puissances du nombre d'or >>> Nombres de 1 à 20 en base Phi >>> Cas de2025	Débutants Nombre d'or Glossaire Nombre d'or

Approche		haut
Paradoxal ? Il semble paradoxal de pouvoir compter en base Phi, le nombre d'or, car celui-ci comporte une racine de 5 dans son expression. Couple L'astuce consiste à éliminer les racines de 5. Comment ? En impliquant le conjugué du nombre d'or. Par exemple, la différence des deux vaut 1, un nombre entier. Le nombre 1 en base Phi se note: [1, 1]𝝋 Pour exprimer le nombre n en base Phi, il faut trouver la bonne combinaison des d'entiers dont la somme vaut n, tout en comptant autant de racines de 5 en positif et en négatif.	Le nombre d'or est irrationnel Conjugué du nombre d'or Différence

Cas singulier du 1

Nous venons de voir que: 𝝋 – 1/𝝋 = 1

Une autre possibilité inattendue: 1/𝝋 + 1/𝝋² = 1

On en déduit , en additionnat, que: 𝝋 + 1/𝝋² = 2

Calcul

La puissance -1 produit une racine de 5 positive tandis que la

puissance -2 en produit une négative. Les deux se compensent, avec effet d'isoler un nombre entier.

Puissances du nombre d'or

haut

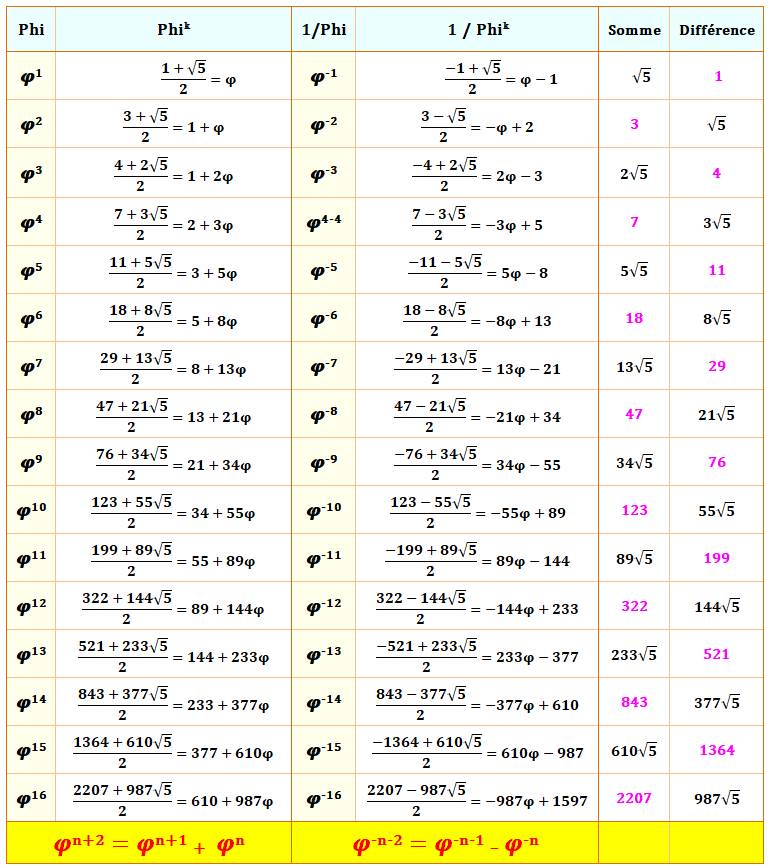
Le tableau présente les puissances de 1 à 16 du nombre d'or et celles de son inverse. Chaque nouvelle puissance se déduit des deux précédentes comme dans le procédé Fibonacci. A droite, on donne la somme et la différence des nombres de la même ligne: même puissances de Phi en positif et en négatif. Les nombres entiers en rose sont les nombres de Lucas: 1, 3, 4, 7, 11, 18, 29, … Chacun de ces nombres est égal à la somme des deux précédents.

Nombres de 1 à 20 en base Phi	haut
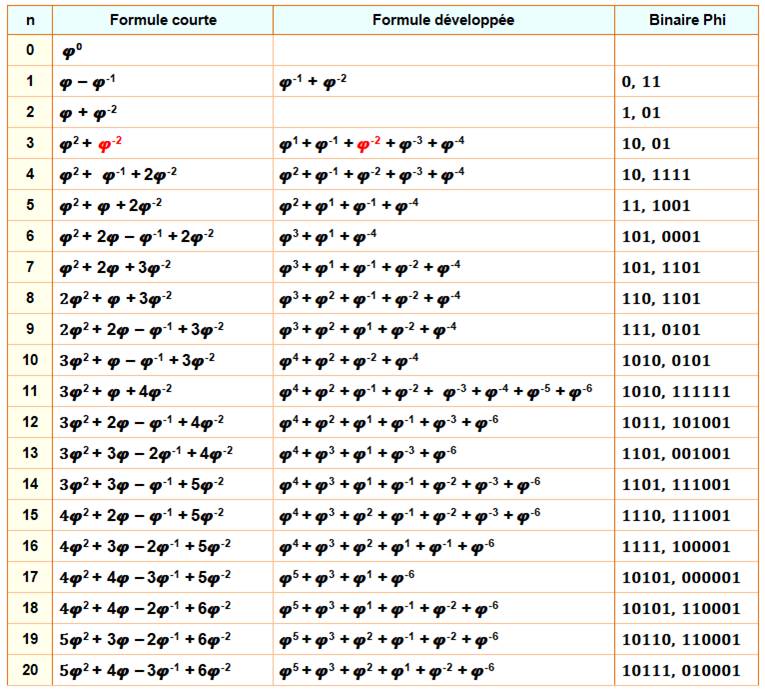
Le tableau présente la numération des nombres de 1 à 20 en base Phi sous trois formes: Formule courte ou somme pondérée des seules puissances 1 et 2 du nombre d'or; Formule développée: somme des puissances du nombre d'or (avec coefficient 1); et Notation binaire en base Phi.

Cas de 2025

Comme tous les nombres, le nombre 2025 peut s'exprimer en base Phi.

Les lignes 2 et 3, montrent le calcul des coefficients entiers (a) et celui des coefficients en racine de 5 (b).

En binaire: 101001000010101,0000010000100001

Formule courte: 559𝝋² + 347𝝋 – 346𝝋^-1 + 560𝝋^-2

Calcul avec Maple (radsimp permet l'élimination des radicaux au dénominateur):

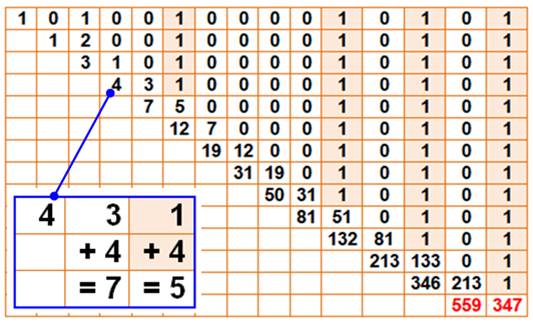
Calcul des coefficients de Phi² et Phi à partir de la valeur binaire

Le coefficient de droite transmet son poids à droite et encore à droite.

Exemple avec le nombre 4 qui ajoute 4 aux deux cases suivantes.

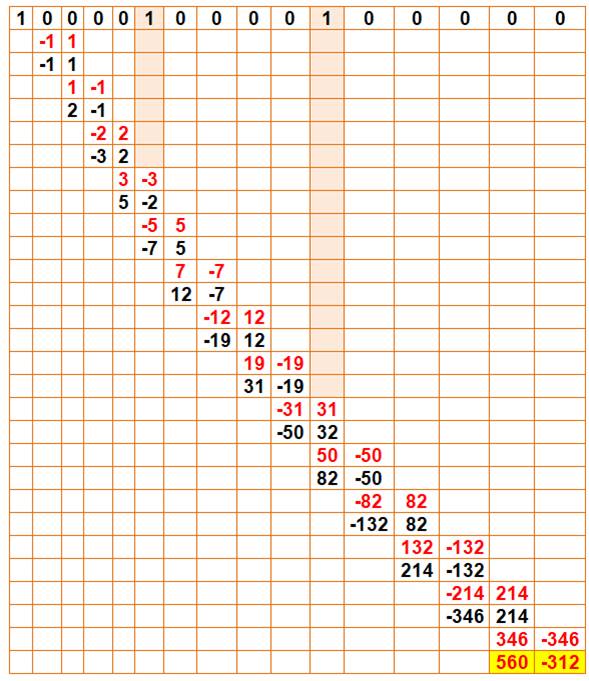
Calcul des coefficients de Phi^-1 et Phi^-2.

La valeur binaire décimale est inversée (premier calcul avec Phi^-16).

Le coefficient de droite transmet son poids en moins à droite et en plus au suivant.

Les lignes en rouge montre la transmission des valeurs

Haut de page (ou double-clic)

Suite	Deux cercles dans un carré – Calcul des rayons Deux cercles dans un carré – Divers défis Géométrie et nombre d'or Valeurs du nombre d'or Construction Trigonométrie
Voir	Cercle Constante Pi Constantes Mathématiques Construction géométrique des nombres Série du type Fibonacci et cousins
Sites	Representation of integers as powers of golden ratio How do I show that every positive integer can be written as a finite sum of distinct integral powers of the golden ratio?
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Geometri/NbOrNume.htm