![]()
|
|
Ce site est désormais accessible en http://diconombre.fr/index.html et
pour cette page voir le lien en fin de page |
|
22 Novembre 2025
![]()
|
Création du: 14/10/2024 Édition du: 03/12/2025 |
|
Dictionnaire des Nombres |
|||
|
1 / 10 / 50 / 100
/ 500 / 1000 / 1500 / 1900 / 2000 / 2016 / 2017 / 2018 / 2019
/ |
2025 |
2031 à
2099 / 3000 / 5000 / 10 000 / 20 000 / 50 000 / 100 000 / 106 / 109
/ 10100 Autres |
|
|
2020 / 2021 / 2022
/ 2023 / 2024 / 2025 / 2026 / 2027 / 2028
/ 2029 / 2030 |
|||
![]()
Index 2025 – ONZE pages pour ce nombre exceptionnel
|
Nombre 2025 |
||
|
Humour 2024-2025 |
Chiffres de 2025
(jeu) |
Faites
un double-clic pour un retour en haut de
page
Le nombre 2025 et
culture générale
|
2,025 103 |
|
|
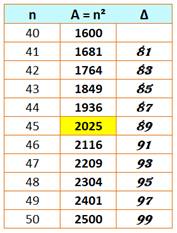
2 025: Nombre
remarquable et année remarquable Première année carrée (2 025 = 45²) depuis 1936 (= 44²). La prochaine en
2116 = 46². Si la précédente année carrée fut 1936 = 44², un tournant
véritable historique, quel est le présage pour cette présente année carrée ? Année Nicomaque: carré de la somme des nombres de 1 à n
= somme des cubes des nombres de 1 à n.
Propriété
générale: Voir Théorèmes de
Nicomaque de Gérase Année Kaprekar 2 025
= (20 + 25)² = 45² Année des impairs 2 025
= 1 + 3 + 5 + 7 + … + 87 + 89 Voir Calendrier et humour 2025 Âge carré Les
personnes nées en 1980 ont 45 ans en 2 025, un âge
qui est la racine carrée de l'année en cours. Il
faudra attendre une naissance en 2070 pour que cela se reproduise avec 46 ans. Auguste De Morgan est né en
1806 et il a eu 43 ans en 1849 = 43². Voir Carré de l'âge Table de multiplication &
Rectangles La somme
des nombres de la table de
multiplication des nombres de 1 à 9 est égale à 2025. Il y a 2025 rectangles
dans une grille carrée de 45×45 Une jour particulier, celui de la
fêtes des mères
|
En guise de bonne année 2025
|
A la Saint-Sylvestre, à
minuit moins dix secondes, décompte à partir de 9 jusqu'à 0, additionne ces 10
chiffres, met la somme au carré et te voilà en 2025 ! (9
+ 8 + 7 + 6 + 5 + 4+ 3 + 2 + 1 + 0)² =
2025 Carré pannumérique |
|
Merci à l'auteur: Rachid
Boudjenane
Voir Nombre
géométrique
|
Année qui commence par un mercredi et se termine
par un mercredi. L'année
compte 365 jours soir 52 semaines et un jour. Un seul
vendredi 13, le 13 juin 2025. C'est la 2025e année de
notre ère, la 25e année du IIIe millénaire
et du XXIe siècle et la 6e année de la décennie 2020-2029. Première année carrée (2025 =
45²) depuis 1936 (= 44²).
Du 8 au 17 mars: Jeux Olympiques
d'hiver à Turin. L’Organisation des Nations Unies
(ONU) a officiellement déclaré 2025 Année internationale de la science et de
la technologie quantiques
(IYQ2025), coïncidant avec le 100e anniversaire de la mécanique
quantique. Du 10 au 19 mars 2025: La semaine
des mathématiques organisée par le ministère de l’Éducation nationale. Thème:
Maths hors les murs: montrer l'importance des mathématiques
dans la vie quotidienne et leur utilisation dans divers contextes pratiques. Voir
Année 2025 en humour |
||
|
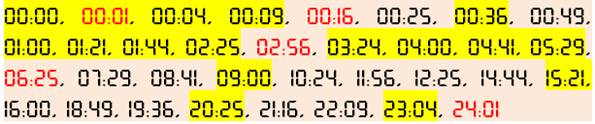
Un des 34 carrés qui peuvent figurer sur votre réveil
numérique:
En rouge,
les cas où le nombre est une puissance quatrième, En jaune,
la somme des chiffres est également un carré. Pas
d'heure carrée pour les 13h et les 17h. Seule
heure cube: |
Voir Brève 61-1210
SUITE SUR LE
NOMBRE 2025 voir index en Haut de page (ou double-clic)
![]()
|
Voir Nom des nombres
|
|
|
Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques
SUITE SUR LE
NOMBRE 2025 voir index en Haut de page (ou double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Sites |
|
|
Cette page |
![]()