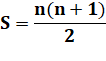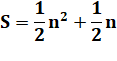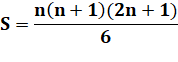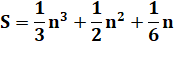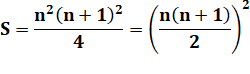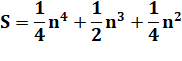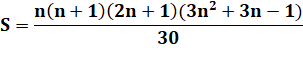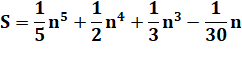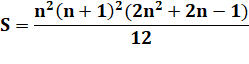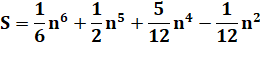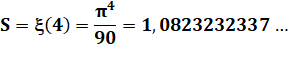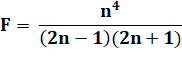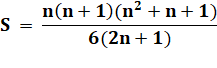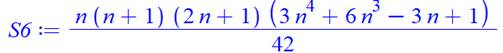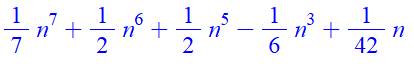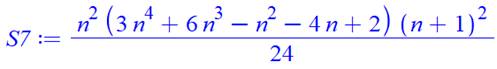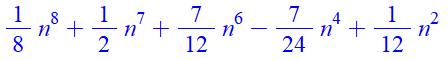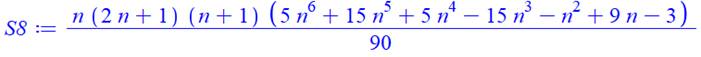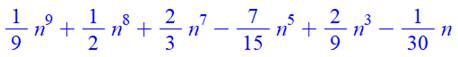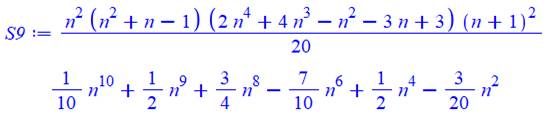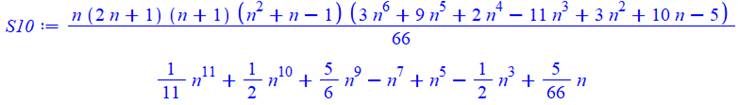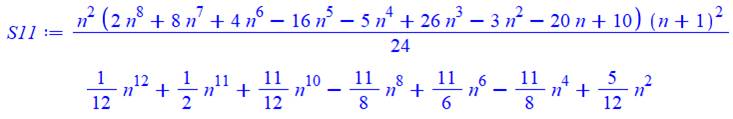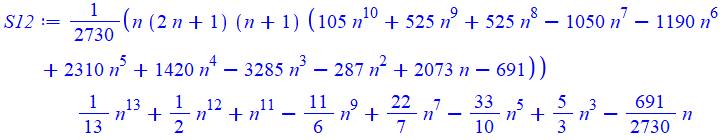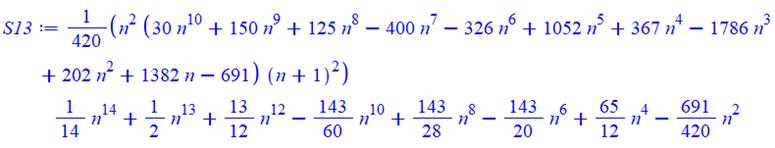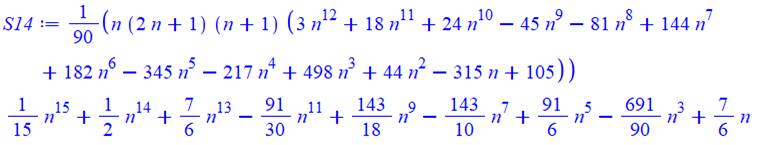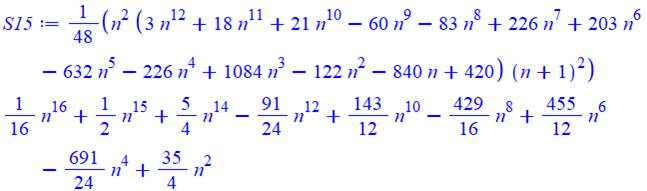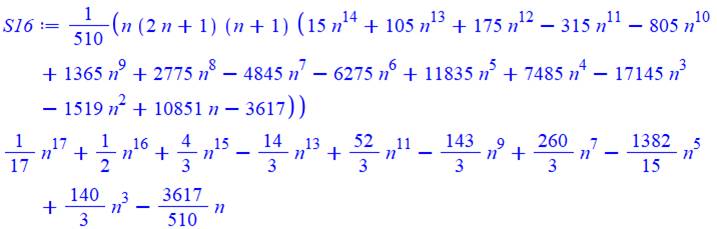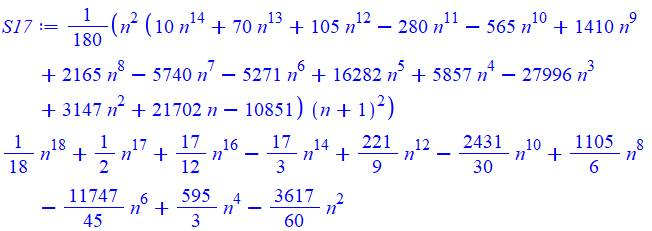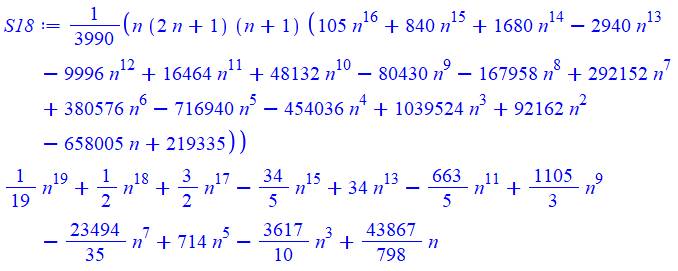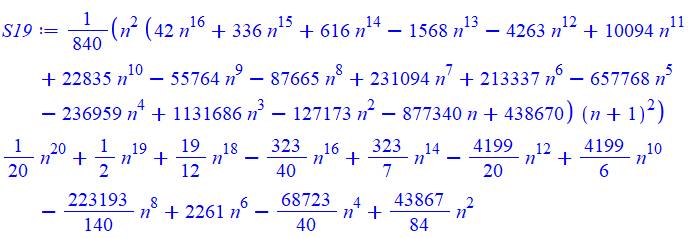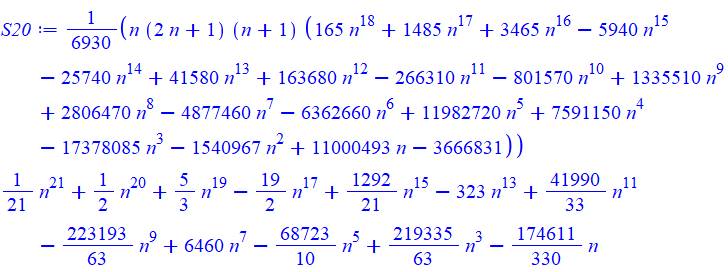NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 19/02/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	IDENTITÉS
Débutants Somme	SOMMES Nombres et puissances					Glossaire Addition
INDEX Sommes Calcul Identités	Index et Bases		Entiers	Carrés	Cubes
	Somme des puissances de 2 à 20 des nombres successifs
	Somme des puissances de nombres en progression arithmétique
	Nombre somme de puissances
	Somme d'un nombre à des puissances successives
	Somme d'expression en x et puissances successives
		Sommaire de cette page >>> Somme des puissances de 1 à 5 >>> Formules en puissance 4

SOMMES des NOMBRES CONSÉCUTIFS

à la puissance k

Table donnant la somme des entiers de 1 à n, chacun porté à la puissance k. Les coefficients qui caractérisent ces formules sont des nombres de Bernoulli.

Sommes des puissances de 1 à 5
1		S(k = 5) = 1 + 2 + 3 + 4 + 5= 15 Somme des entiers
2		S(k = 5) = 1^2 + 2^2 + 3^2 + 4^2 + 5^2= 55 Somme des carrés
3		S(k = 5) = 1^3 + 2^3 + 3^3 + 4^3 + 5^3= 225 Somme des cubes
4		S(k = 5) = 1^4 + 2^4 + 3^4 + 4^4 + 5^4= 979 Somme des puissances 4
5		S(k = 5) = 1^5 + 2^5 + 3^5 + 4^5 + 5^5= 4 425

Somme des PUISSANCES 4
Puissance 4	1^4 + 2^4 + 3^4 +… + n^4
Inverses	1/1^4 + 1/2^4 + 1/3^4 …
Inverses produits Impairs	S = 1^4/ (1.3) + 2^4/ (3.5) + … + F avec

Nouvelle version du 3 octobre 2019 avec n = quantité de nombres de 1 à n
Les formules données précédemment comptaient le 0 en plus, comme dans les calculs avec les coefficients de Bernoulli

Grand merci à Michel Desmonts

Sommes des puissances de 6 à 20
6	Forme factorisée Forme développée
7
8
9

10
11
12
13
14

15
16
17
18
19
20

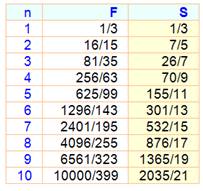
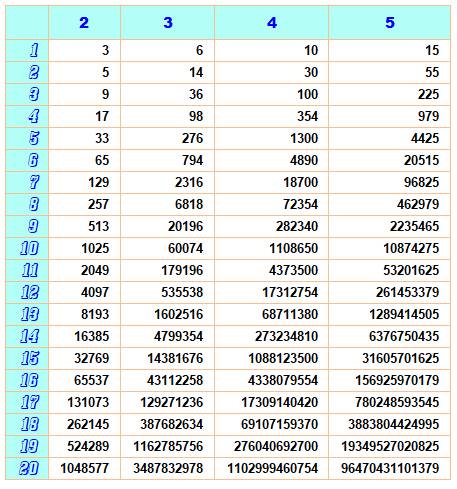
Table pour la somme des puissances de 1 à 20

et une quantité de nombres n de 2 à 5

Exemple de lecture: 1³ + 2³ + 3³ + 4³ = 100; 1⁴ + 2⁴ + 3⁴ = 98

Suite de cette table / Cas de puissances successives

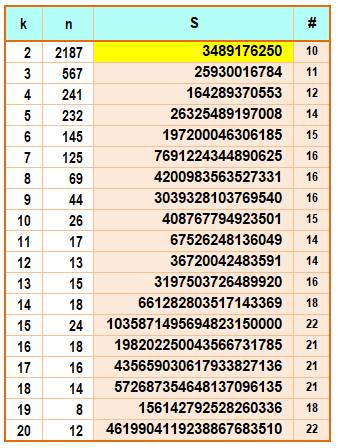
Liste des sommes pannumériques de puissance k jusqu'au nombre n

Exemple de lecture: 1² + 2² + 3² + … + 2187² = 3489176250, nombre qui comporte (#) 10 chiffres.

C'est d'ailleurs la seule somme exactement pannumérique

Retour	Sommes des cubes
Suite	Puissances des nombres avec 2, 3, 5 … Somme des puissances de nombres en progression arithmétique Toutes les formules de somme
Table	Carrés, cubes … et leurs cumuls
Voir	Carrés Constantes Cubes Factorielles et somme des entiers Isopérimètre Nombres consécutifs Index Nombres géométriques Pairs et impairs Tautochronie Théorèmes
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Identite/SomPuisT.htm