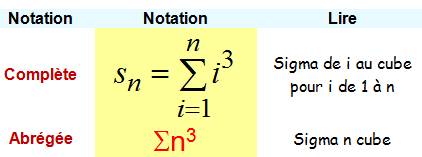![]()
|
|
Ce site est désormais accessible en http://diconombre.fr/index.html et
pour cette page voir le lien en fin de page For
this page, refer to the link at the bottom. |
|
22 Novembre 2025
![]()
|
|||||||||||||||||||||||||||||||||
![]()
|
SOMME des NOMBRES Démonstrations directes Méthode générale pour calculer la somme des entiers, des carrés, des
cubes, etc. Elle repose sur l'utilisation d'une équation
bien choisie au départ. N'oubliez
pas que la méthode
la plus simple pour calculer la somme des entiers est encore la méthode utilisée par Gauss
enfant. |
Voir Démonstration par
induction / Principe de cette
démonstration
|
|
|||
|
Entiers |
1 + 2 + 3 … |
= 1/2
n (n + 1) = Tn |
|
|
Carrés |
12 + 22
+ 32 … |
= 1/6
n (n + 1)(2n + 1) |
|
|
Cubes |
13 + 23
+ 33 … |
= Tn2 |
|
|
Puissance 4 |
14 + 24
+ 34 … |
=
1/30 n (n + 1) (2n + 1) (3n² + 3n – 1) |
|
Voir Toutes les
formules pour les sommes
|
|
|||
|
Nous
cherchons la valeur de la somme des entiers naturels jusqu'à n Sn
= 1 + 2 + 3 … + n |
|
||
|
Principe Nous avons besoin d'un point de
départ (d'une astuce). Nous la trouvons dans le
développement du carré de la somme de deux nombres: (a + b)² = a²+ 2ab
+ b² Ici, on prendra deux nombres
successifs: a et a + 1,
ce qui donne: b = 1 Un astucieux effet de sommes
successives va ensuite, faire disparaître pratiquement tous les termes au
carré. |
|||
|
Calcul |
|
||
|
Équation de départ |
(a + 1)² |
= a² + 2a + 1 |
|
|
Mettons sous cette forme |
(a + 1)² – a² |
= 2a + 1 |
|
|
Calculons pour a = 1 |
2²
– 1² |
= 2.1
+ 1 |
|
|
Pour a = 2 |
3²
– 2² |
= 2.2
+ 1 |
|
|
Pour a = 3 |
4²
– 3² |
= 2.3
+ 1 |
|
|
Ainsi de suite |
… |
|
|
|
Jusqu'à a = n |
(n +
1)² – n² |
= 2.n
+ 1 |
|
|
Somme de toutes ces lignes (marron).
Dans la colonne de gauche, les carrés
s'éliminent deux à deux. |
(n +
1)² – 1² |
= 2
(1 + 2 + 3 +… n) + (1 + 1 + 1n fois) = 2A
+ B |
|
|
Première parenthèse (A) |
A |
=
(1+2+3+…n) = = la somme cherchée |
|
|
Seconde parenthèse B): la somme de n
fois 1 est n |
B |
= (1
+ 1 + 1n fois) = n |
|
|
Reprenons notre somme |
(n + 1)² –
1² |
= 2A + B = 2. |
|
|
En arrangeant |
2. |
= (n
+ 1)² – 1² – n = n²
+ 2n + 1 – 1 – n = n²
+ n = n(n
+ 1) |
|
|
Et finalement |
|
= 1/2 n(n + 1) |
|
|
Vérification
avec n = 1 |
|
= 1/2 x 1 x2 = 1 |
|
Voir Démonstration
semblable, plus courte
|
|
||||
|
Nous cherchons la valeur de la somme
des carrés des entiers naturels
jusqu'à n. Sn = 1² + 2² + 3² … +
n² |
|
|||
|
Principe Même principe que pour les entiers.
Nous allons utiliser le développement non plus du carré, mais celui du cube
de la somme de deux nombres: (a + b)3
= a3 + 3a2 b + 3a b2 + b3 Toujours avec b = 1 |
||||
|
Calcul |
|
|||
|
Équation de départ |
(a + 1)3 |
= a3 + 3a2 + 3a + 1 |
||
|
Mettons sous cette forme |
(a + 1)3 – a3 |
= 3a2 + 3a + 1 |
||
|
Calculons pour a = 1 |
23
– 13 |
= 3.12 + 3.1
+ 1 |
||
|
Pour a = 2 |
33
– 23 |
= 3.22 + 3.2
+ 1 |
||
|
Pour a = 3 |
43
– 33 |
= 3.32 + 3.3
+ 1 |
||
|
Ainsi de suite |
… |
|
||
|
Jusqu'à a = n |
(n +
1)3 – n3 |
= 3n2
+ 3n + 1 |
||
|
Somme de toutes ces lignes Colonne de gauche: les cubes s'éliminent deux à deux |
(n +
1)3 – 13 |
= 3(1² + 2² + 3² … + n² ) + 3 (1 + 2 + 3 +…
n) + (1 + 1 + 1n
fois) = 3A + 3B + C |
||
|
|
A |
= (1²
+ 2² + 3² … + n² ) = = la somme cherchée |
||
|
|
B |
= (1
+ 2 + 3 + … n) = = 1/2 n(n + 1) |
||
|
|
C |
=
(1+1+1n fois) = n |
||
|
Reprenons notre somme |
(n + 1)3 – 1 |
= 3A + 3B + C = 3. |
||
|
En isolant la somme n² |
3. |
= (n +
1)3 – 1 – 3/2 n(n + 1) – n |
||
|
En arrangeant |
6. |
= 2(n
+ 1)3 – 2 – 3 n(n + 1) – 2n = 2(n3
+ 3 n² + 3n + 1) – 2 – 3n² – 3n – 2n = 2n3
+ 3n² + n = n
(2n² + 3n + 1) = n
(n + 1) (2n + 1) |
||
|
Et finalement |
|
= 1/6 n(n + 1)(2n + 1) |
||
|
Vérification
avec n = 1 |
|
= 1/6 x 1 x 2 x 3 = 1 |
||
|
|
||||
|
Nous cherchons la valeur de la somme
des cubes des entiers naturels jusqu'à n. Sn = 13 +
23 + 33 … + n3 |
|
|||
|
Principe Vous l'avez compris Pour le cube, on prend la puissance
supérieure. On se souvient du triangle
de Pascal. 1 1 2 1 1 3 3 1 1 4 6 4 1 Soit le développement de la
puissance 4 (a + b)4 = a4 + 4a3
b + 6a2 b2 + 4a b3 + b4 Toujours avec b = 1 |
||||
|
Calcul |
|
|||
|
Équation de départ |
(a + 1)4 |
= a4 + 4a3 + 6a2 +
4a + 1 |
||
|
Mettons sous cette forme |
(a + 1)4 – a4 |
= 4a3 + 6a2 + 4a + 1 |
||
|
Calculons pour a = 1 |
24
– 14 |
= 4.13
+ 6.12 + 4.1 + 1 |
||
|
Pour a = 2 |
34
– 24 |
= 4.23
+ 6.22 + 4.2 + 1 |
||
|
Pour a = 3 |
44
– 34 |
= 4.33
+ 6.32 + 4.3 + 1 |
||
|
Ainsi de suite |
… |
|
||
|
Jusqu'à a = n |
(n + 1)4 –
n4 |
= 4n3 + 6n2 + 4n+ 1 |
||
|
Somme de toutes ces lignes Colonne de gauche:
les puissances 4 s'éliminent deux à deux |
(n +
1)4 – 14 |
= 4(13 + 23 + 33 …
+ n3 ) 6(1²+2²+3² … + n² ) + 4 (1+2+3+…n) + (1+1+1n fois) = 4A + 6B + 4C + D |
||
|
|
A |
= (13
+ 23 + 33 … + n3 ) = = la somme cherchée |
||
|
|
B |
=
(1²+2²+3² … + n² ) = = 1/6 n(n + 1)(2n + 1) |
||
|
|
C |
=
(1+2+3+…n) = = 1/2 n(n + 1) |
||
|
|
D |
=
(1+1+1n fois) = n |
||
|
Reprenons notre somme |
(n + 1)4 – 1 |
= 4A + 6B + 4C + D = 4. |
||
|
En arrangeant Etc. |
4. |
= (n
+ 1)4 – 1 – n(n
+ 1)(2n + 1) – 2 n(n + 1)
– n |
||
|
Et finalement |
|
= { 1/2 n(n+1)}² |
||
|
Vérification
avec n = 1 |
|
= (1/2 x 1 x 2)² = 1 |
||
|
|
||||
|
Nous cherchons la valeur de la somme
des cubes des entiers naturels jusqu'à n. Sn = 14 +
24 + 34 … + n4 |
|
|||
|
Principe 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10
5 1 Soit le développement de la
puissance 5: (a + b)5 = a5 + 5a4
b + 10a3 b2 + 10a2 b3 + 5a b4
+ b5 Avec b = 1 |
||||
|
Calcul |
|
|||
|
Équation de départ |
(a + b)5 |
= a5 + 5a4 + 10a3 +
10a2 + 5a + 1 |
||
|
Mettons sous cette forme |
(a + b)5 – a5 |
= 5a4 + 10a3 + 10a2
+ 5a + 1 |
||
|
Calculons pour a = 1 |
25
– 15 |
= 5.14
+ 10.13 + 10.12 + 5.1 + 1 |
||
|
Pour a = 2 |
35
– 25 |
= 5.24
+ 10.23 + 10.22 + 5.2 + 1 |
||
|
Pour a = 3 |
45
– 35 |
= 5.34
+ 10.33 + 10.32 + 5.3 + 1 |
||
|
Ainsi de suite |
… |
|
||
|
Jusqu'à a = n |
(n +
1)5 – n5 |
= 5n4
+ 10n3 + 10n2 + 5n + 1 |
||
|
Somme de toutes ces lignes Colonne de gauche:
les puissances 5 s'éliminent deux à deux |
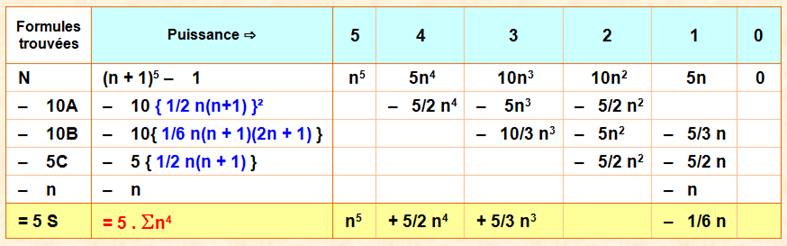
(n + 1)5 – 15 N |
= 5. = 5S + 10A + 10B + 5C
+ n |
||
|
|
S |
= = la somme cherchée |
||
|
|
A |
= = { 1/2 n(n+1)}² |
||
|
|
B |
= = 1/6 n(n + 1)(2n + 1) |
||
|
|
C |
= = 1/2 n(n + 1) |
||
|
Calculons avec un peu d'ordre !
|
||||
|
Vérification
avec n = 1 |
5. |
= 1 + 5/2 + 5/3 - 1/6 = 5 |
||
|
Et
finalement, la formule |
|
= 1/30 (6n5 + 15n4 +
10n3 - n) = 1/30 n (n+1) (2n+1) (3n²+3n–1 ) |
||
|
Notons
que dans cette formule se trouve celle des carrés |
|
= 1/30 n (n+1) (2n+1) (3n²+3n-1) = 1/5 {1/6 n (n+1) (2n+1)}
(3n²+3n-1) = 1/5 (3n²+3n-1) . |
||
Suite
|
Outre
l'aspect laborieux, il est possible d'étendre ce principe à toutes les
puissances. |
Voir Toutes les formules de sommes
jusqu'à la puissance 20
Merci à Jean Bétréma pour ses indications
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()