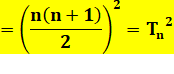![]()
|
|
Ce site est désormais accessible en http://diconombre.fr/index.html et
pour cette page voir le lien en fin de page For
this page, refer to the link at the bottom. |
|
22 Novembre 2025
![]()
|
||||||||||||||||||||||||||||||||||||||||
![]()
|
SOMMES des CUBES avec nombres consécutifs |
Voir Cubes / Somme de k cubes
/ Somme des trois
cubes
|
|
||||
|
Cubes |
13
+ 23 + … + n3 |
= 1/4 n² (n + 1)²
|
||
|
Cubes pairs |
23
+ 43 + … + (2n)3 |
= 2 n² (n +
1)² |
||
|
Cubes impairs |
13
+ 33 + … + (2n –
1)3 |
= n² (2n² –
1) |
||
|
(1) Inverses |
1/13 + 1/23 +
1/33 … |
= 1,20205689… = |
||
|
(2) Inverses pairs |
1/23 + 1/43 +
1/63 … |
= 0,15025711… |
||
|
(3) Inverses impairs (1)-(2) |
1/13 + 1/33 +
1/53 … |
= 1,05179978… |
||
|
|
(4) Inverses alternés (3)-(2) |
1/13 – 1/23 +
1/33 – … |
= 0,90154267… |
|
|
|
(5) Inverses pairs alternés |
1/23 – 1/43 +
1/63 – … |
= 0,11269283… |
|
|
|
(6) Inverses impairs alternés |
1/13 – 1/33 +
1/53 – … |
= 0,96894614… |
|
|
|
Quinconce |
13 + 3.22 + 33 + 3.42 + 53 + 3.62 + 73 … + T Impair => T = n3 Pair => T = (n–1)
n² |
n pair S = 1/8 n(n3+4n²+10n+8) n impair S = 1/8 (n+1) (n3+7n²–3n–1) |
|
|
|
Cubes en progression arithmétique |
S = 53 + 113 +
173 + 233 = 18 536 F = 5 L= 23 = F + (n-1) r n = 4 r = 6 Voir Brève 535 |
T = 1/2 n (F + L) S = r.T2
+ T.F (F – r) |
|
|
|||
|
Cubes
Voir Développements et démonstration Autre démonstration (par induction) Conséquence
évidente: La somme des cubes des nombres consécutifs est divisible par la somme
de ces nombres. En effet: 13 + 23 + 33
+ … + n3 = (1 +
2 + 3 + … + n) (1 + 2 + 3 + … +
n) 13 + 23 + 33
= 36 = (1 + 2 + 3) (1 + 2 + 3) = 6 x 6 P
|
|||
|
|
||
|
Problème
Solution
|
|
|
|
Tableau donnant la quantité de cubes et la
hauteur
Avec 2500 cubes, il est
possible de construire une pyramide jusqu'à l'ordre 9, soit 45 cm de haut
avec exactement 2025 cubes. Il en reste 2500 – 2025 = 475. Somme des cubes Nous venons de calculer la
somme cumulée des cubes et la somme cumulée des entiers (les nombres
triangulaires). Les deux sommes sont l'une le carré de l'autre.
Ainsi 45² = 2025. |
||
|
|
||||
|
Divisible
par 2n+1 |
= (2n + 1)
(n² + n + 1) |
23
+ 33 = 5 x 7 = 35 33
+ 43 = 7 x 13 = 91 43
+ 53 = 9 x 21 = 189 |
||
|
Divisible
par 3n Divisible par 9 |
= 3n
(n² + 2) |
13 + 23 + 33 = 6 x
6 =
36 23 + 33 + 43 = 11
x 9 = 99 33 + 43 + 53 = 12 x 18
=
216 Voir Divisiblité par 9 |
||
|
Carré
somme de trois cubes consécutifs (Trois seuls cas jusqu'à au moins un million) |
9 = 3² = 03
+ 13 + 23 36 = 6² = 13 + 23
+ 33 41 616 = 204² = 233 + 243 + 253 |
|||
|
Cube
sommes de trois cubes
consécutifs |
216 = 63
= 33 + 43 + 53 59 6503
= 413583 + 413593 + 413603 119 3003
= 827173 + 827183 + 827193 Etc. (très nombreux) |
|||
|
Divisible
par 2(2n+3) |
= 2(2n
+ 3) (n² + 3n + 6) |
13 + 23 + 33 + 43
= 10 x 10 = 100 23 + 33 + 43 + 53
= 14 x 16 = 224 33 + 43 + 53 + 63
= 18 x 24 = 432 |
||
|
Divisible
par 5n |
= 5n
(n² + 6) 13 + 23 + 33 + 43
+ 53 = 15 x 15 = 225 23 + 33 + 43 + 53
+ 63 = 20 x 22 = 440 33 + 43 + 53 + 63
+ 73 = 25 x 31 = 775 |
|||
|
|
= 3
(2n + 5) (n² + 5n + 15) 13 + 23 + 33 + 43
+ 53 + 63 = 21 x 21 = 441 23 + 33 + 43 + 53
+ 63 + 73 = 27 x 29 = 783 33 + 43 + 53 + 63
+ 73 + 83 = 33 x 39 = 1287 |
|||
Nombres sommes de cubes consécutifs
|
Liste
jusqu'à 5000 1, 8, 9,
27, 35, 36, 64, 91, 99, 100, 125, 189, 216, 224, 225, 341, 343, 405, 432,
440, 441, 512, 559, 684,
729, 748, 775, 783, 784, 855, 1000, 1071, 1196, 1241,
1260, 1287, 1295, 1296, 1331, 1584, 1728, 1729, 1800, 1925, 1989, 2016, 2024, 2025, 2197, 2241, 2331, 2584,
2744, 2800, 2925, 2989, 3016, 3024, 3025, 3059, 3060, 3375, 3572, 3915, 3925,
4059, 4096, 4131, 4256, 4320, 4347, 4355, 4356, 4788, 4913, 4941. Liste
des partitions jusqu'à 1000
|
Suite Sommes de cubes
consécutifs
|
|
|||
|
Peut
être premier Multiple
de 6 plus 1 |
= 3n² – 3n + 1 = 3n (n – 1) + 1 |
Voir
Nombre cubains |
|
|
Donne
6n |
= 6n |
|
|
|
Donne
18n |
= 18n 13 –
23 – 43 +
53 = 18 x 3 = 54 23 –
33 – 53 +
63 = 18 x 4 = 72 |
||
|
L'écart
de 3e niveau entre cubes est égal à 6 |
= 6
|
||
Voir Machine de Babbage
|
|
||
|
Somme de cubes = carré La somme
des cubes des nombres de 1 à n est égale à:
Soit le nombre
triangulaire d'ordre n au carré. Conséquence: toutes les sommes de cubes consécutifs commençant par 1
sont des carrés. Exemple: 13 + 23 + 33 = 62
= 36 Le plus petit carré avec premier terme différent de 1 est: 93 + 103 + … + 253 = 3232
= 104 329 |
a,
b, q, S,
S2 q = quantité de termes Avec premier nombre = 1 1, 2, 2, 3, 9 1, 3, 3, 6, 36 1, 4, 4, 10, 100 1, 5, 5, 15, 225 … Avec premier nombre différent de 1 9, 25, 17, 323, 104329 14, 25, 12, 312, 97344 23, 25, 3, 204, 41616 25, 29, 5, 315, 99225 14, 34, 21, 588, 345744 28, 35, 8, 504, 254016 25, 39, 15, 720, 518400 33, 65, 33, 2079, 4322241 69, 100, 32, 4472, 19998784 96, 100, 5, 2170, 4708900 |
|
|
Somme de cubes = cube La somme des cubes des nombres de a à b est égale à:
Exemple Somme des cubes de 6 à 69 et calcul de sa racine cubique:
Lecture de la table 33 + 43 + 53 = 63 = 216 113 + 123 + 133 + 143 = 203
= 8000 63 + 73 + …+ 693 = 1803 =
5 832 000 |
a,
b, q, S, S3 q = quantité de termes 3, 5, 3, 6, 216 3, 22, 20, 40,
64000 6, 30, 25, 60,
216000 15, 34, 20, 70,
343000 6, 69, 64, 180,
5832000 11, 109, 99, 330,
35937000 34, 158, 125, 540,
157464000 291, 339, 49, 1155,
1540798875 213, 365, 153, 1581,
3951805941 213, 555, 343, 2856, 23295638016 273, 560, 288, 2856, 23295638016 556, 654, 99, 2805, 22069810125 646, 798, 153, 3876, 58230605376 406, 917, 512, 5544, 170400029184 |
|
|
|
||
Voir Nombre 180 /
Nombre 216
Table
des nombres, somme de
trois cubes consécutifs / Nombres somme
de 1 à 5 cubes
![]()
|
Suite |
|
|
Table |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()