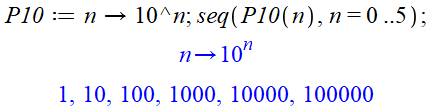NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 02/11/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Nombres
Débutants Général	PETITS & GRANDS				Glossaire Général
INDEX Nombres	Petits et grands nombres		Puissances de dix	P10 (suite)
	Puissance de deux		P10 et multimédia	Échelle de dix
		Sommaire de cette page >>> Puissances de 10 et les chiffres >>> SOMME des puissances de dix >>> VITESSE de PROGRESSION des puissances de dix >>> Nombre premiers autour de 10^n >>> Nombres en k . 10^k + 1

Un gars m'a dit avoir déjà vu un sans-papier manger une mille-feuille arrosé d'un Saint—Émilion. Oui, mais c'était ailleurs, à mille yards. Nous qui nous billions !

Voir Pensées & humour / Alphabet parlant

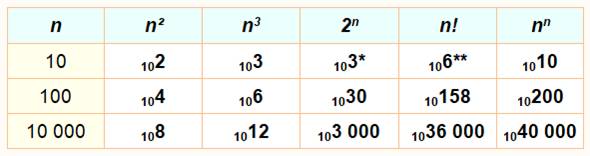
Puissances de DIX

Voir au préalable la Page principale

Séquence des puissances de 10 avec Maple

Instruction à recopier dans Maple

P10:=n->10^n; seq(P10(n), n=0..5);

Programme et exécution

Voir Programmation " séquence"

Puissance de 10 et les chiffres

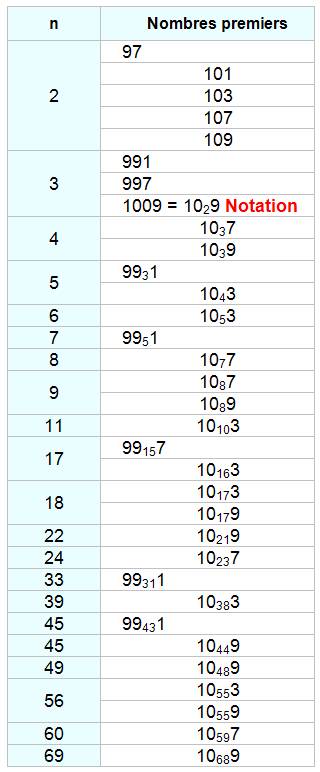
Les puissances n de 10 peuvent s'écrire 2^n x 5^n. Nous cherchons tous ces produits n'ayant aucun zéro, aucun 1, aucun 2, etc. Notez qu'il n'existe aucun cas sans le chiffre 2 ou le chiffre 5. Car toutes les puissances de 5 se terminent par 25. Table donnant les facteurs de 10^n sans un chiffre donné (n testé jusqu'à 1 000) Par exemple, 10^33 est la plus grande telle puissance de 10 connue sans 0 dans ses deux facteurs. Réf. Madachy 1979 / C. Pickover: Keys to Infinity, p. 135, Wiley, 1996 et: Oh, Encore des nombres! p.105, Dunod, 2002 Voir Brève 776 Après 33 et jusqu'à au moins 1000, la seule puissance de 5 sans zéro est 58 (qui vaut 3,5… 10^40). Par contre la puissance 2^58 comporte un 0.

Voir Tables / Nombre 10¹⁸ /Nombre 10³³

SOMME des PUISSANCE de DIX

9,14… 10 ³¹

= 91 409 924 241 424 243 424 241 924 242 500

= 1¹⁰ + 2¹⁰ +3¹⁰ + … + 1000¹⁰

Somme de puissances dixièmes des entiers successifs.

Calcul effectué par Jacques Bernoulli (1654 - 1705), en moins de 10 minutes. Il utilise une méthode de calcul rapide inventée par lui.

Valeurs de cette fonction

n	= 1^10 + 2^10 + 3^10 + … + n^10
1	1
2	1025
3	60074
4	1108650
5	10874275
6	71340451
7	353815700
8	1427557524
9	4914341925
10	14914341925
20	24163571680850
30	1922052927013775
40	43591205959337700
50	494346993683649625
60	3608881215962946550
70	19421693680720225475
80	83570850731150483400
90	303039084670532717325
100	959924142434241924250
200	1913444835685168480848500
300	164011579554029702713772750
400	3865650888058579936937697000
500	44879113391808743371149621250
600	332847212306551932305346545500
700	1811727156737115565039525469750
800	7862830386369679067073683394000
900	28702898078161021872307817318250
1000	91409924241424243424241924242500

Vitesse de progression pour les PUISSANCES DE DIX

Tableau donnant les valeurs des fonctions indiquées pour n = 10, 100 et 10 000. On donne une valeur approchée en notant uniquement la valeur de la puissance de dix: 102 veut dire 10² = 100; 103 veut dire 10^3 =1 000; Etc. Valeurs exactes * 2^10 = 1, 024 10^3 10^3 ** 10! = 3, 626 800 10^6 Exemples de lecture: n = 10 : 2^n = 2^10 = 1 024 => 10^3 n = 100 : 2^n = 2^100 => 10^30 n = 10 000 : n! = 10 000! => 10^36 000

NOMBRES PREMIERS autour de 10^n 10
Aucun autre nombre premier jusqu'à n = 100 dans cet intervalle de plus ou moins 10.

Nombres k . 10^k + 1

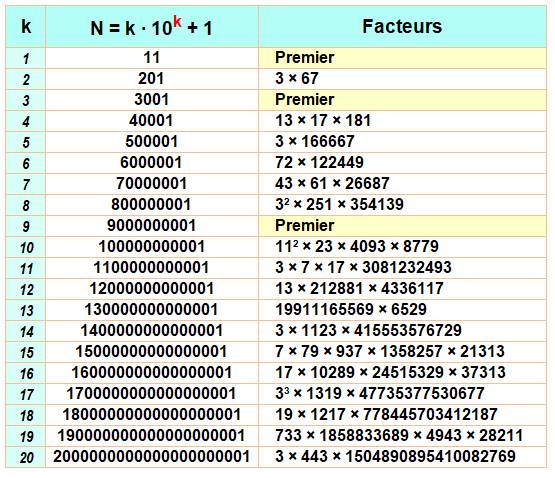
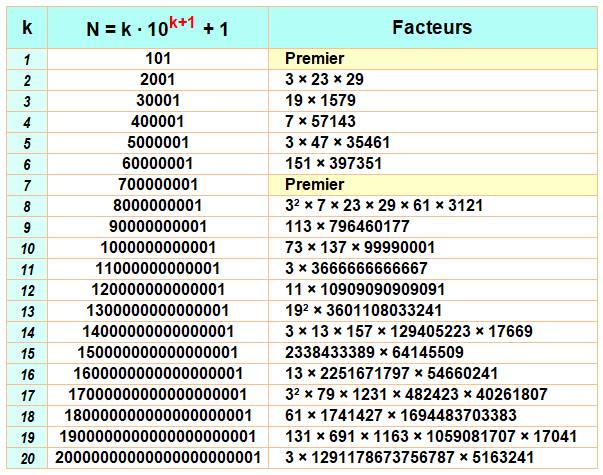
Premiers pour k = (1, 3, 9, 21, 363) jusqu'à k = 1000

Premiers pour k = (1, 7, 39) jusqu'à k = 1000

Voir	Addition Évolution des puissances de 9 et de 2 Fractions en 1 / (10^k – n) Gogol = 10^100 Petits et grands nombres Puissance de deux Puissances – Index Somme des entiers Sommes des nombres de 1 à 10^k – Astuce
Site	OEIS A175188 – Smallest composite numbers of the form k*10^k + 1
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Nombre/Puiss10.htm