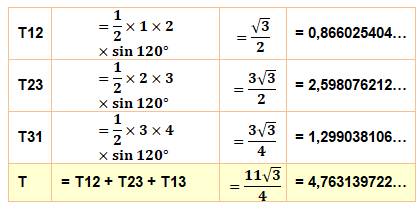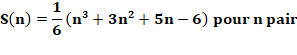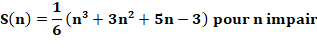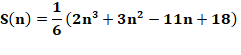Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 05/01/2024 M'écrire Brèves de Maths

INDEX Motifs Types de nombres	Types de Nombres – Motifs
	Uniformes	Ondulants	Répétitions	Formes diverses
	Croissants	Ascendants	Zébrés	Zigzag
	Orphelins	Multiples	Radar

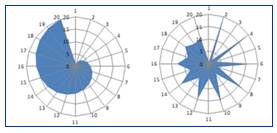
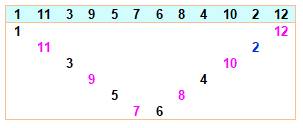
Nombres en RADAR Aire min et max sous radar Pour un nombre donné n, un cercle est divisé en n rayons. Sur chaque rayon, on place les nombres de 1 à n de façons variées. En joignant ces points, on forme un polygone. Quelles sont les façons qui produisent un polygone d'aire minimale ou d'aire maximale ? Ce problème revient à minimiser ou maximaliser la somme des produits de paires de nombres pris parmi les nombres de 1 à n. Ex: avec 1234 => la permutation 1324 minimise la somme-produit: S = 1×3 + 3×2 + 2×4 + 4×1 = 21.
	Sommaire de cette page >>> Approche pour n = 3 >>> Cas n = 4 >>> Cas n = 5 >>> Cas n = 6 >>> Cas général – Minimum >>> Cas général – Maximum	Débutants Nombres Glossaire Nombres

Approche pour n = 3		haut
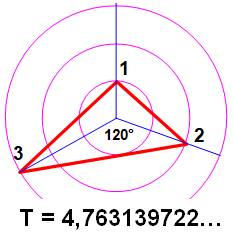
Construction Trois cercles concentriques de rayon 1, 2 et 3. Trois rayons à 120° les uns des autres. On trace le triangle avec pour sommet les points 1, 2 et 3 sur chacun des rayons. Aire du triangle L'aire du triangle est égale au demi-produit des côtés et du sinus de l'angle embrassé. Le triangle rouge est composé de trois triangles élémentaires, chacun ayant un angle de 120° et dont les côtés de l'angle sont connus. On peut donc en calculer l'aire. Calculs Remarque Il existe une seconde configuration symétrique (1, 3, 2). 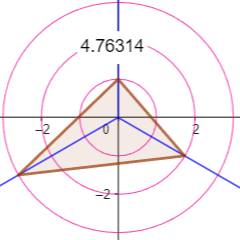Dans les deux cas: aire minimale = aire maximale = 4,76 …	Radar des nombres1, 2 et 3 Vérification avec GeoGebra

Cas pour n = 4		haut
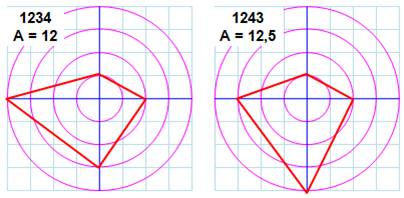
Construction Même principe avec quatre rayons à 90°. Dans ce cas, les aires sont plus faciles à calculer car: sinus 90° = 1. Exemple de calcul pour 1234 Trois possibilités Le point en 1 étant fixé, il existe six permutations des nombres 2, 3, 4. Elles sont symétriques deux à deux: Soit les trois cas de l'illustration comme cas primitifs. Les trois autres s'en déduisent par symétrie par rapport à l'axe vertical.	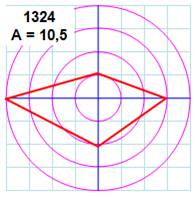Radar des nombres1, 2, 3 et 4 Aire = somme des produits successifs L'aire du quadrilatère rouge vaut la somme des produits des sommets pris par couples successifs. Avec 1 2 3 4 Aire = ½ sin90° (1×2 + 2×3 + 3×4 + 4×1) Aire minimale: 10,5 avec 1324 Aire maximale: 12,5 avec 1243

Cas pour n = 5		haut
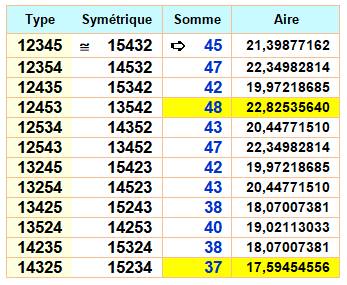
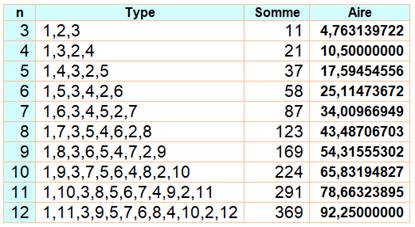
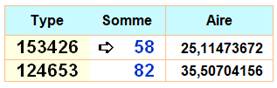
Construction Même principe avec cinq rayons à 72°. Dans ce cas: sinus (72°) = 0,95105… Dénombrement des cas Toutes les permutations des nombres commençant par 1 et comprenant les nombres 2 à 5 sont recevables. Sur ce tableau 12 cas primitifs et 12 cas symétriques. On donne la somme des produits et l'aire du pentagone résultant. 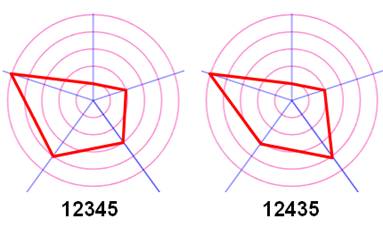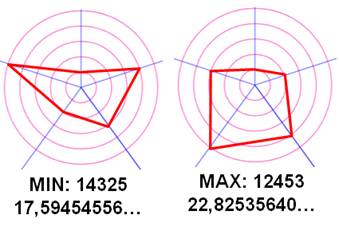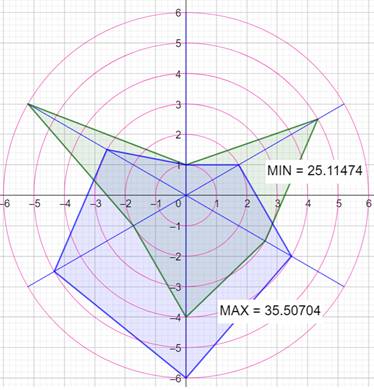Somme = somme des produits des couples des nombres successifs: S = 1×2 + 2×3 + 3×4 + 4×5 + 5×1 = 45	Radar des nombres1, 2, 3, 4 et 5 – Exemples Configuration min max

Cas pour n = 6		haut
Construction Même principe avec six rayons à 60°. Dénombrement des cas Il y a 5! = 120 permutations de cinq nombres (le sixième étant fixé) et la moitié sont symétriques par rapport à la verticale et encore la moitié par rapport à l'horizontale. Soit 30 cas primitifs. Configuration min max Sélection obtenue par logiciel. Facile à écrire. En revanche, les tests au-delà de n = 12 nécessitent un long temps de calcul.	Configuration min max

Cas général – Minimum		haut
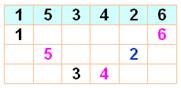
Tableaux Ces deux tableaux ont été établis avec l'utilisation d'un logiciel. Cas de l'aire minimale Observez l'alternance des nombres pour n = 6: Le premier couple d'extrêmes (1 et 6) est placé aux extrémités. Le deuxième couple d'extrêmes (2 et 5) est placé aux extrêmes suivants, mais en inversant. Etc. Cas de n = 12 pour vérification	Configuration MIN pour n de 3 à 12 Liste des produits-sommes minimum 1, 4, 11, 21, 37, 58, 87, 123, 169, 224, 291, 369, 461, 566, 687, 823, 977, 1148, 1339, 1549, 1781, 2034, 2311, 2611, 2937, 3288, 3667, 4073, 4509, 4974, 5471, 5999, 6561, 7156, 7787, 8453, 9157, 9898, 10679, 11499, 12361, 13264, 14211, 15201, 16237, … Formules

Cas général – Maximum		haut
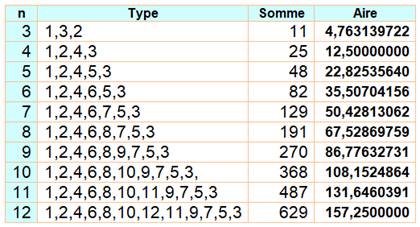
Cas de l'aire maximale Observez la suite des nombres pairs et celle des nombres impairs. Règle de composition de la configuration Départ avec 1. Suite croissante des nombres pairs. suite décroissante des nombres impairs Vérification pour n = 20 Configuration: [1, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 19, 17, 15, 13, 11, 9, 7, 5, 3]. Somme-produit: 2833 Conforme à la liste de tels nombres.	Configuration MAX pour n de 3 à 12 Liste des produits-sommes maximums 1, 4, 11, 25, 48, 82, 129, 191, 270, 368, 487, 629, 796, 990, 1213, 1467, 1754, 2076, 2435, 2833, 3272, 3754, 4281, 4855, 5478, 6152, 6879, 7661, 8500, 9398, 10357, 11379, 12466, 13620, 14843, 16137, 17504, 18946, 20465, 22063, 23742, 25504, … Formules

Merci à Michel THIOLLIER pour l'idée de cette page

Haut de page

Suite	Uniformes Orphelins
Voir	Motifs Nombres consécutifs – Index
Sites	OEIS A110611 – Minimal value of sum(p(i)p(i+1),i=1..n), where p(n+1)=p(1), as p ranges over all permutations of {1,2,...,n} OEIS A110610 – Maximal value of sum(p(i)p(i+1),i=1..n), where p(n+1)=p(1), as p ranges over all permutations of {1,2,...,n} OEIS A0664842 – Maximal value of Sum_{i=1..n} (p(i) - p(i+1))^2, where p(n+1) = p(1), as p ranges over all permutations of {1, 2, ..., n}
Cette page	http://villemin.gerard.free.fr/aNombre/MOTIF/Chiffres/Radar.htm