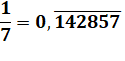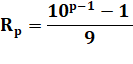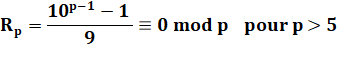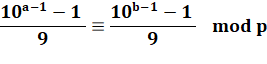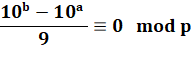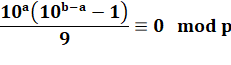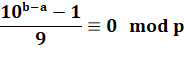collection de nombres, rep-unit et leurs divisions

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 31/10/2022 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	MOTIFS & FORMES
Débutants Général	REPDIGIT				Glossaire Général
INDEX Formes et motifs Nombres en chiffres Chiffres Types de nombres	Repdigits		Repunits	Presque repdigit
	999 …		Division des Repunits	Division de 999 …
	Nombres trompeurs		(n.p) min = Repdigit
		Sommaire de cette page >>> Divisibilité des repunits par un nombre premier >>> Nombres trompeurs >>> Division des Repunits par les Repunits >>> Classement par rapports successifs >>> Classement par rapport à la partie décimale en 9 >>> Nombres semi-uniformes

DIVISION des nombres uniformes

Divisibilité des repunits par un nombre premier
Théorème Tout nombre premier supérieur à 5 divise un repunit formé de p – 1 fois le chiffre"1". Le nombre premier 7 divise le repunit de longueur 6.	Exemples
Période la fraction Elle est égale à 9 fois le quotient du repunit.
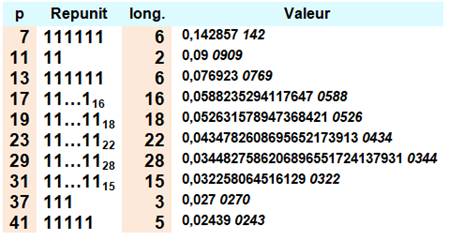
Théorème La période de 1/p, pour p > 5, est égale à la longueur du plus petit repunit divisible par p. Le nombre premier 37 divise le repunit 111; la période du développement décimal de 1/37 est de longueur 3. La période maximale est p – 1.	Exemples

Voir Brève 812 / Nombres trompeurs

Facteurs de R_k-1

Entre accolades, les facteurs du repunit ayant k–1 fois le chiffre "1".

2, {}

3, {11}

5, {11, 101} sont les facteurs de 1111 comportant 4 (= 5–1) fois le "1".

7, {3, 7, 11, 13, 37}

11, {11, 41, 271, 9091}

13, {3, 7, 11, 13, 37, 101, 9901}

17, {11, 17, 73, 101, 137, 5882353}

19, {3, 7, 11, 13, 19, 37, 52579, 333667}

23, {11, 23, 4093, 8779, 21649, 513239}

29, {11, 29, 101, 239, 281, 4649, 909091, 121499449}

Listes ordonnées de ces facteurs

3, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 101, 127, 137, 139, 211, 239, 241, 271, 281, 521, 859, 1933, 2161, 2531, 2689, 3191, 3541, 4093, 4649, 8779, 9091, 9901, 16763, 21649, 27961, 43037, 52579, 62003, 123551, 333667, 459691, 513239, 909091, 1676321, 2906161, 4147571, 4188901, 5882353, 10838689, 39526741, 121499449, 265371653, 599144041, 1058313049, 5964848081, 77843839397, 183411838171, 999999000001,

Nombres trompeurs (deceptive numbers)

Sur la même idée concernant les repunits, R. Francis et T.Ray nomment deceptive numbers, les nombres composés n qui divisent les repunit d'ordre n – 1 (R_n-1).

Le plus petit est 91 qui divise R₉₀. En effet 91 est compos" (7×13) et divise 11…1₉₀.

Liste des nombres trompeurs

91, 259, 451, 481, 703, 1729, 2821, 2981, …

Suite Page spéciale Nombres trompeurs

Démonstration courte du premier théorème
Repunit Ils peuvent se mettre sous cette forme:
Petit théorème de Fermat Le petit théorème de Fermat s'applique si les nombres a et p sont premiers entre eux.
Application directe
Conséquence

Démonstration sans Fermat
Les restes de la division des repunit par p sont compris entre 0 et p-1. Il existe plus d'un repunit dont la division par p produit le même reste.	Repunits distincts comprenant a et b chiffres "1" et ayant le même reste lorsque divisés par p. Avec leur forme canonique on peut écrire:
Ou en ramenant tout du même côté
Factorisation en posant a > b
Division par 10^a à condition que le diviseur soit premier avec 10, excluant 2 et 5.
Conclusion si p > 5 Note: 111 est divisible par 3.	Il existe un repunit qui est divisible par p.

DIVISION des nombres uniformes par des nombres uniformes

Travaux pratiques

DIVISION des repunits par les repunits

R₁	/	*R'₁*	=	*N entier*	*ou N en décimal*
11		1		11
111		11			10, 0909090909
11 11		11		101
11 11		111			10, 0090090090
11 1 11		11			1010, 09090909
11 1 11		111			100, 099099099
11 1 11		11 11			10, 0009000900
111 111		11		10101
111 111		111		1001
111 111		11 11			100, 009900990
111 111		11 1 11			10, 0000900009
111 1 111		11			101010, 090909
111 1 111		111			10010, 0090090
111 1 111		11 11			1000, 09990999
111 1 111		11 1 11			100, 000990010
111 1 111		111 111			10, 0000090000
111 11 111		11		1010101
111 11 111		111			100100, 099099
111 11 111		11 11		10001
111 11 111		11 1 11			1000, 00999010
111 11 111		111 111			100, 000099000
111 11 111		111 1 111			10, 0000009000
111 111 111		11			10101010, 0909
111 111 111		111		1001001
111 111 111		11 11			100010, 000900
111 111 111		11 1 11			10000, 0999909
111 111 111		111 111			1000, 00099900
111 111 111		111 1 111			100, 000009900
111 111 111		111 11 111			10, 0000000900
11 111 111 11		11		101010101
11 111 111 11		111			10010010, 0090
11 111 111 11		11 11			1000100, 00990
11 111 111 11		11 1 11		100001
11 111 111 11		111 111			10000, 0099990
11 111 111 11		111 1 111			1000, 00009990
11 111 111 11		111 11 111			100, 000000990
11 111 111 11		111 111 111			10, 0000000090

CLASSEMENT PAR RAPPORTS SUCCESSIFS

R₁	/	*R'₁*	=	N	*10ⁿ*
11 111 111 11		111 111 111		1,00000000090	1
111 111 111		111 11 111		1,00000000900	1
11 111 111 11		111 11 111		1,00000000990	2
111 11 111		111 1 111		1,00000009000	1
111 111 111		111 1 111		1,00000009900	2
11 111 111 11		111 1 111		1,00000009990	3
111 1 111		111 111		1,00000090000	1
111 11 111		111 111		1,00000099000	2
111 111 111		111 111		1,00000099900	3
11 111 111 11		111 111		1,00000099990	4
111 111		11 1 11		1,00000900009	1
111 1 111		11 1 11		1,00000990010	2
111 11 111		11 1 11		1,00000999010	3
111 111 111		11 1 11		1,00000999909	4
11 111 111 11		11 1 11		1,00001	5
11 1 11		11 11		1,00009000900	1
111 111		11 11		1,00009900990	2
111 1 111		11 11		1,00009990999	3
111 11 111		11 11		1,0001	4
111 111 111		11 11		1,00010000900	5
11 111 111 11		11 11		1,00010000990	6
11 11		111		1,00090090090	1
11 1 11		111		1,00099099099	2
111 111		111		1,001	1
111 1 111		111		1,00100090090	4
111 11 111		111		1,00100099099	5
111 111 111		111		1,001001	6
11 111 111 11		111		1,00100100090	7
111		11		1,00909090909	1
11 11		11		1,01	2
11 1 11		11		1,01009090909	3
111 111		11		1,0101	4
111 1 111		11		1,01010090909	5
111 11 111		11		1,010101	6
111 111 111		11		1,01010100909	7
11 111 111 11		11		1,01010101	8
11		1		1,1	1

CLASSEMENT PAR RAPPORT

À LA PARTIE DÉCIMALE EN 9

R₁	*R'₁*	*Partie décimale du rapport*
1111111111	111111111	.90000000090000000090e-8
111111111	11111111	.90000000900000009000e-7
11111111	1111111	.90000009000000900000e-6
1111111	111111	.90000090000090000090e-5
111111	11111	.90000900009000090000e-4
11111	1111	.90009000900090009000e-3
111111111	1111	.90009000900090009000e-3
1111	111	.90090090090090090090e-2
1111111	111	.90090090090090090090e-2
1111111111	111	.90090090090090090090e-2
111	11	.90909090909090909090e-1
11111	11	.90909090909090909090e-1
1111111	11	.90909090909090909090e-1
111111111	11	.90909090909090909090e-1
1111111111	11111111	.99000000990000009900e-6
111111111	1111111	.99000009900000990000e-5
11111111	111111	.99000099000099000099e-4
1111111	11111	.99000990009900099000e-3
111111	1111	.99009900990099009900e-2
1111111111	1111	.99009900990099009900e-2
11111	111	.99099099099099099099e-1
11111111	111	.99099099099099099099e-1
1111111111	1111111	.99900009990000999000e-4
111111111	111111	.99900099900099900099e-3
11111111	11111	.99900999009990099900e-2
1111111	1111	.99909990999099909990e-1
1111111111	111111	.99990099990099990099e-2
111111111	11111	.99990999909999099990e-1

Nombres semi-uniformes

Un nombre semi-uniforme n'est composé que de deux chiffres.

Le nombre 22 332 est le plus petit divisible par chacun de ses chiffres et dont la somme des chiffres est aussi divisible par les deux chiffres.

Suite

Nombres trompeurs

Division de 999 …

Divisibilité par un repunit

Divisibilité des nombres permutés

Voir

Cette page

http://villemin.gerard.free.fr/Wwwgvmm/Formes/RepUnDiv.htm