|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
NOMBRES PALINDROMES
Monsieur, prénom et nom, SVP? LÉON NOËL |
Voir Anacyclique
|
Trouver
la somme de tous les palindromes à trois chiffres divisibles par 13. |
|
En 2016, Cilleruelo, Luca et Baxter
prouvent que: Tout nombre est la somme de trois palindromes en base
b (b > 4). For integer b > 4, any positive integer can be written as a
sum of three palindromes in base b. Exemple: 389 = 11 + 55 +
323 En 2017,
A. Rajasekaran, J. Shallit, T. Smith complètent: Tout nombre est la somme d'au plus quatre nombres naturels dont la représentation en base 2 est un palindrome. Résultats similaires
pour les bases 3 et 4. Exemples
|
Voir Somme de
trois nombres triangulaires (théorème des nombres polygonaux)
Brève
47-931
|
|
|||||||||
|
MOTS
PALINDROMES Les mots
palindromes sont des mots à symétrie bilatérale (qui s'épellent de
la même façon dans les deux sens) Exemples RADAR ROTOR ÉTÉ Une phrase complète
possédant une symétrie bilatérale est un palindrome. Exemple ÉSOPE
RESTE ICI ET SE REPOSE NOMBRES
PALINDROMES Un nombre
palindrome est un nombre qui garde la même
valeur quand on prend ses
chiffres à l'envers. Exemples 11 101 45654 12345678987654321 Voir Nombres
palindromes ANNÉES
PALINDROMES
Voir Dates palindromes |
|||||||||
|
|
|||||||
|
0 |
|
101 |
1001 |
10001 |
100001 |
... |
|
|
1 |
11 |
111 |
1111 |
10101 |
101101 |
|
|
|
2 |
22 |
121 |
1221 |
10201 |
102201 |
|
|
|
3 |
33 |
131 |
1331 |
10301 |
... |
|
|
|
4 |
44 |
141 |
1441 |
10401 |
|
|
|
|
5 |
55 |
151 |
1551 |
10501 |
|
|
|
|
6 |
66 |
161 |
1661 |
10601 |
… |
|
|
|
7 |
77 |
171 |
1771 |
10701 |
765567 |
… |
|
|
8 |
88 |
181 |
1881 |
10801 |
… |
|
|
|
9 |
99 |
191 |
1991 |
10901 |
|
|
|
|
|
202 |
2002 |
11011 |
|
|
|
|
|
|
212 |
2112 |
11111 |
|
|
|
|
|
|
222 |
2222 |
11211 |
|
|
|
|
|
|
232 |
2332 |
11311 |
|
|
|
|
|
|
242 |
2442 |
11411 |
|
|
|
|
|
|
252 |
2552 |
11511 |
|
|
|
|
|
|
262 |
2662 |
11611 |
|
|
|
|
|
|
272 |
2772 |
11711 |
|
|
|
|
|
|
282 |
2882 |
11811 |
|
|
|
|
|
|
292 |
2992 |
11911 |
|
|
|
|
|
|
303 |
3003 |
12021 |
|
|
|
|
|
|
313 |
3113 |
12121 |
|
|
|
|
|
|
... |
... |
... |
|
|
|
|
|
|
979 |
9779 |
99799 |
|
|
|
|
|
|
989 |
9889 |
99899 |
|
|
|
|
|
|
999 |
9999 |
99999 |
|
|
|
|
Voir Tables
Devinette
|
Quel
est le palindrome suivant? Un
automobiliste constate que son compteur indique un kilométrage palindromique:
15 951 km. Coïncidence, pile poil une heure plus tard, il constate qu'il
vient d'atteindre le palindrome suivant! Quelle est sa vitesse? Pour
calculer le palindrome suivant, il faut partir du centre et ajouter 1. Le
9 devient 0 et les chiffres de chaque
côté sont incrémentés en 6. Soit 15 9 51 qui devient 16 0 61 km. La
différence est égale à 110 et sa vitesse est de 110 km/h. |
|
|
||
|
Quelques
propriétés Pratiquement
toutes les questions intéressantes sur les nombres
premiers palindromes sont encore sans
réponse. On n'a même pas
démontré qu'il y en a une infinité... Somme 38 + 83 = 121 Produit
du nombre et son retourné 1089 x 9 = 9801 2178 x 4 = 8712 10989 x 9 = 98901 21978 x 4 = 87912 109989 x 9 = 989901 219978 x 4 = 879912 Les seuls à 4, 5,
6, etc. chiffres avec ce motif. On
note que 2178 est le double de 1089. Le
motif sous-jacent est le suivant, encore un coup des repunits: 1089 = 11 x
11 x 9 et 9801 = 11 x
11 x 9 x 9 10989 = 111 x
11 x 9 et 98901 = 111 x
11 x 9 x 9 109989 = 1111 x
11 x 9 et 989901 = 1111 x
11 x 9 x 9 Même
motif avec 3 chiffres: trois cas seulement (hors triviaux) 510 = 015 x 34 540 = 045 x
12 810 = 018 x
45 Voir Nombres de
Friedman / Nombres retournés Retourné d'un nombre et
palindrome |
||
|
|
Les
opérations (en vert) son l'image l'une de l'autre par retournement. |
|
|
Quelques
curiosités Le plus grand
nombre non palindrome connu (5 juillet 2024 –
Patrick De Geest) dont le carré
est un palindrome est:
Le plus grand
nombre non palindrome qui était connu en 1997 dont le carré
est un palindrome était:
Les cubes
palindromiques dont les racines cubiques ne sont pas des palindromes sont
si rares que l'on n'en connaît qu'un:
Une
somme avec 4 palindromes premiers à 5 chiffres
Il existe bon
nombre de telles curiosités Note: 30503 n'est pas
premier. Chiffre
unique Les Repdigits (ex: 666) et Repunits
(ex: 1111) sont, bien évidemment, des palindromes à
un seul chiffre. |
|
|
|
|
Propriété Tous les palindromes sont des sommes de
multiples de 102k+1 +1 Exemples k = 0 101 + 1 = 11 k
= 1 103 + 1
= 1001 k = 2 105 + 1 = 100001 3223 = 3 x (103 +1) + 20 x
(101 +1) Voir Exemple d'emploi |
|
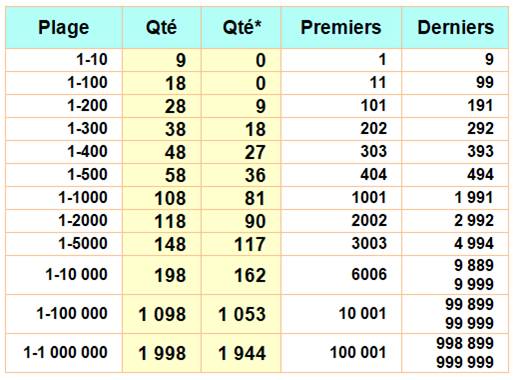
Quantité de palindromes (*sans les repdigits)
|
|
|
|
Tous les palindromes à nombre pair de chiffres sont divisibles par 11. Exemples 8 8 = 11 x 8 45 54 = 11 x 414 789 987 = 11 x
71817 987 6 6 789 = 11 x
8 978 799 Voir Démonstration |
|
|
|
||
|
Facteurs
sans exposants Exemple:
6006 = 2 x 3 x 7 x 11x 13. Le plus petit palindrome
parmi tous les palindromes à cinq facteurs sans exposant (sans puissance).
|
Facteurs
avec exposants Exemple:
88 est le
palindrome le plus petit à quatre facteurs, y compris répétés.
|
|
Voir Repdigits – Records
|
|
|
|
On
cherche les nombres palindromes qui sont premiers. Unique 11 est le seul nombre palindrome
premier a avoir un nombre de chiffres pair. Propriétés Un nombre premier palindrome doit commencer
et finir avec 1, 3, 7 ou 9 et avoir un
nombre impair de chiffres. Rappel : Avec un nombre
pair, c'est multiple de 11. Les
premiers PALINDROMES PREMIERS Il y en a 15 à 3 chiffres 101 131 151 181 191 313 353 373 383 727 757 787 797 919 929 Il y en a 0 à 4 chiffres Il y en a 93 à 5 chiffres 10301 10501 10601
11311 11411 12421 12721 128 ... Il y en a 0 à 6 chiffres Il y a 668 palindromes premiers de 7 chiffres Il
y a 83 duos de palindromes premiers jumeaux dont 3 sont triplés et 1
quadruplé. Duos 1092901 –
1093901 1177711 –
1178711 1242421 – 1243421 ... Triplés 1968691 - 1969691 -
1970791 ... Quadruplé 1878781 – 1879781 –
1880881 – 1881881 Curiosité 777 8 777 Plus petit premier
palindrome de 7 chiffres avec les chiffres 7
& 8. Le
plus petit premier pannumérique 102 345 698 7 896
543 201 Voir Pannumérique / Diconombre Le plus petit palindrome premier de rang palindrome 143 787 341 est
premier de rang 81 14 118. On a aussi 11 de
rang 5, trivial. |
|
|
|
|||||||
|
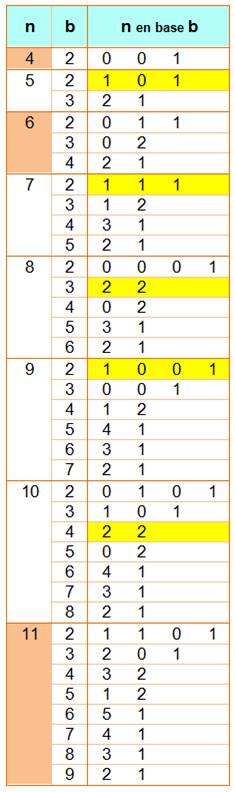
Définition Nombre n qui, dans toutes les bases
de 2 à n – 2, n'est jamais palindrome. Exemples (Voir Tableau) Pour
n = 4, la seule base à considérer est la base 2 et, en binaire,
4 vaut 100 (chiffre indiqué à l'envers
sur le tableau). Ce nombre binaire n'est pas palindrome. Le nombre 4 est
strictement non palindrome. Pour
n = 5, sa valeur binaire (101) est un palindrome (jaune). Le nombre 5 n'est
pas strictement palindrome. Pour
n = 6, pas de palindrome en base 2, 3 et 4. Le nombre 6 est strictement non
palindrome (marron). Etc. Notes La base n est exclue de la
définition, car n en base n vaut 10 (en effet 1010 = 1010).
Alors, n est toujours non palindrome
en base n. La base n – 1 également, car n
s'écrit alors 11 (en effet: 1010 = 119). Alors, n est toujours palindrome en base n
– 1.
Propriétés Après n = 6, tous ces nombres sont
premiers. Par contre, aucun premier de Mersenne
et Fermat
ne se trouve dans cette catégorie. |
|
||||||
|
Liste des strictement non palindromes jusqu'à n = 10 000 0, 1,
2, 3,
puis: |
|||||||
|
4 6 11 19 47 53 79 103 137 139 149 163 167 179 223 263 269 283 293 311 317 347 359 367 389 439 491 563 569 593 607 659 739 827 853 877 977 983 997 |
1019 1049 1061 1187 1213 1237 1367 1433 1439 1447 1459 1511 1553 1579 1669 1709 1753 1759 1907 1949 1993 1997 2011 2063 2087 2099 2111 2137 2179 2207 2287 2309 2339 2417 2459 |
2503 2657 2677 2683 2693 2713 2749 2897 2963 3023 3089 3119 3229 3253 3259 3323 3371 3407 3449 3547 3559 3583 3623 3643 3833 3847 4007 4073 4091 4099 4139 4157 4211 4283 4337 4339 4349 4391 |
4463 4523 4549 4643 4679 4729 4787 4871 4909 4919 4933 5011 5021 5039 5059 5099 5179 5231 5297 5303 5309 5351 5387 5417 5431 5471 5503 5527 5653 5693 5711 5791 5827 5839 5939 |
6047 6067 6079 6089 6131 6199 6229 6247 6269 6277 6311 6343 6359 6389 6551 6599 6653 6793 6871 6947 6983 6991 7019 7079 7159 7213 7247 7283 7433 7487 7691 7817 7877 7949 7963 |
8017 8069 8089 8123 8147 8221 8243 8287 8291 8293 8423 8539 8573 8669 8699 8783 8863 8941 9043 9059 9067 9173 9209 9227 9277 9337 9341 9377 9419 9421 9533 9587 9643 9689 9739 9781 9887 |
||
Voir Programmation de cette recherche
|
Trouver
la somme de tous les palindromes à trois chiffres divisibles par 13. Solution – Identification
des palindromes N
= Mettons
en évidence le 13 avec 100 = 91 + 9 = 13 x 7 + 9 N
= 13 x 7 a + 10 (a + b) Le
palindrome N est divisible par 13 si chaque terme est divisible. par 13. Or
le premier l'est; le second 10 (a + b) doit l'être. Donc:
a + b = 13k avec a et b de 0 à 9; seule possibilité k = 1. Ce
qui donne les valeurs des palindromes à trois chiffres divisibles par 13: 494, 585, 676, 767, 858 et 949. Calcul de la somme (avec un
peu d'astuce) S
= 444 + 50 + 555 + 30
+ 666 + 10 + 767 – 10
+ 888 – 30 + 999 – 50 S
= 111 (4 + 5 + 6 + 7 + 8 + 9) = 111 x 3 x 13 = 111 x 39 = 3900 + 390 +
39 = 4 329 On aurait pu tenir le
raisonnement voisin pour 11 N = 100a + 10b + a = 99a + 2a + 10b Ce
qui impose: a + 5b = 11k ou a = 11k – 5b
|
|
|
|
|
Aussi |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
Voir site de Patrick De Geest Voir aussi Patrick De
Geest
|
|
Cette page |
