|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
NOMBRES
UNIFORMES ou REPDIGITS selon
base de numération Nombres dont les chiffres sont
répétés lorsqu'ils sont exprimés dans une base b. Certains sont repdigits dans une base
elle-même repdigit. |
Anglais: Rep-digit or Repdigit or Monodigit
|
|
||
|
Le nombre
15 se décline dans toute de bases de 2 à 15 de la manière suivante:
En jaune,
les configurations en repdigit. Ce nombre
et dit brésilien. On
s'intéresse à ces nombres et à la quantité de représentations uniformes. |
Le nombre
17 se décline dans toute de bases de 2 à 17 de la manière suivante:
En jaune,
la seule configuration en repdigit. Ce nombre
et dit NON-brésilien. |
|
Voir Nombres
brésiliens – Propriétés et développements
|
|
||
|
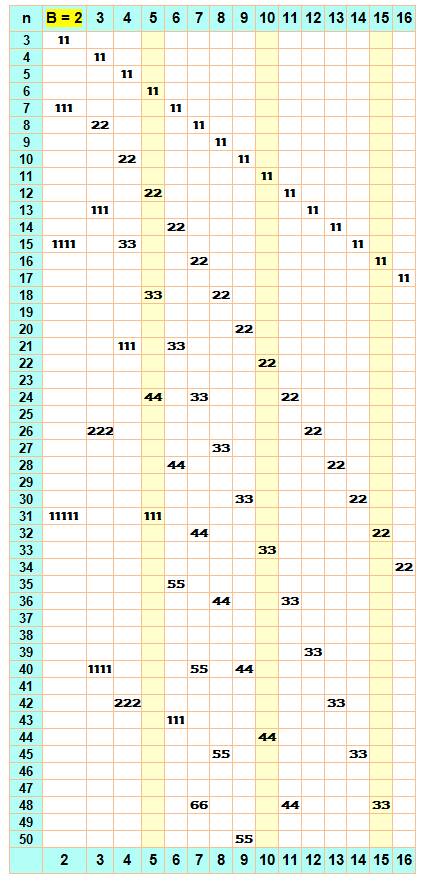
Le
cas binaire (B = 2) On connait les nombres binaires composés de
"1": ce sont les puissances de
2 moins 1. Exemples
de lecture: 3 s'écrit
11 en binaire
(B = 2) et c'est un repdigit 8 en base 3
est le repdigit 22. 24 en base
5 vaut 44, car 4 x 5 + 4 = 24 Propriétés Constat: tous les nombres sont repunits en base n – 1. Les repdigits avec base inférieures à n – 1 sont
appelés nombres brésiliens. Le nombre
est 7 = 1112 est le plus petit. Le nombre
15 = 11112 = 334 est le plus petit doublement
brésilien. Notez
les curiosités:
1210 =1111 ou encore 18010 = 4444. Ces cas ne sont pas rares: 1410 = 1212
, 1610 = 1313 , 1810 = 1414 , 2010
= 1515 , … >>> |
|
|
|
|
||
|
Liste des nombres
qui n'ont aucune représentation uniforme (repdigit) sauf en base n – 1 (triviale). Note:
le nombre 3 = 112 est dans cette liste car la base 2 vaut 3 – 1. |
[3, 4, 5, 6, 9, 11, 17, 19, 23, 25, 29, 37, 41,
47, 49, 53, 59, 61, 67, 71, 79, 83, 89, 97, 101, 103, 107, 109, 113, 131,
137, 139, 149, 151, 163, 167, 169, 173, 179, 181, 191, 193, 197, 199, 223,
227, 229, 233, 239, 251, 257, 263, 269, 271, 277, 281, 283, 289, 293, 311,
313, 317, 331, 337, 347, 349, 353, 359, 361, 367, 373, 379, 383, 389, 397,
401, 409, 419, 431, 433, 439, 443, 449, 457, 461, 467, 479, 487, 491, 499,
503, 509, 521, 523, 529, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599,
607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691,
701, 709, 719, 727, 733, 739, 743, 751, 761, 769, 773, 787, 797,
809, 811, 821, 823, 827, 829, 839, 841, 853, 857, 859, 863, 877, 881, 883,
887, 907, 911, 919, 929, 937, 941, 947, 953, 961, 967, 971, 977, 983, 991,
997] |
|
|
|
|
|
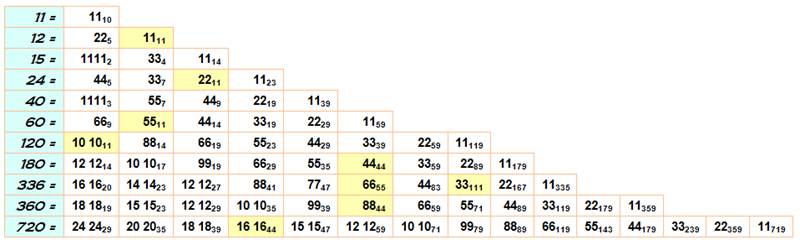
Record de présentations
repdigits en base b (super-brésiliens) (En jaune,
ceux dont la base est aussi repdigit)
|
|
![]()
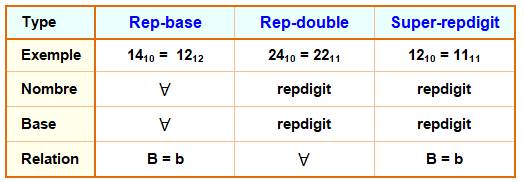
Trois types de nombres selon la base
|
Nombre N base 10 = Nombre B base b
|
|
|
|
|
Nombres
repbases Ils sont tels que le nombre et la base sont égaux. Ce
tableau donne la suite des nombres repbases Lecture 1810 = 1414 |
|
|
|
|||||||||
|
Nombre repdigit avec base
repdigit pour n de 10 à 250 hors super-repdigits Ex: 2310 = 1122 25310 = [11, 11]22 |
23, 11, 22 24, 22, 11 34, 11, 33 36, 33, 11 45, 11, 44 48, 44, 11 56, 11, 55 60, 55, 11 67, 11, 66 68, 22, 33 69, 33, 22 72, 66, 11 |
78, 11, 77 84, 77, 11 89, 11, 88 90, 22, 44 92, 44, 22 96, 88, 11 100, 11, 99 108, 99, 11 112, 22, 55 112, 11, 111 115, 55, 22 |
120, AA, 11 134, 22, 66 135, 33, 44 136, 44, 33 138, 66, 22 156, 22, 77 161, 77, 22 168, 33, 55 170, 55, 33 178, 22, 88 184, 88, 22 |
200, 22, 99 201, 33, 66 204, 66, 33 207, 99, 22 223, 11, 222 224, 44, 55 224, 22, 111 225, 55, 44 230, AA, 22 234, 33, 77 238, 77, 33 |
|||||
|
Suite de 250 à 999 253, [11, 11], 22 266, [2, 2, 2], 11 267, [3, 3], 88 268, [4, 4], 66 270, [6, 6], 44 272, [8, 8], 33 276, [12, 12], 22 299, [13, 13], 22 300, [3, 3], 99 306, [9, 9], 33 312, [4, 4], 77 315, [7, 7], 44 322, [14, 14], 22 334, [1, 1], 333 335, [5, 5], 66 336, [6, 6], 55 336, [3, 3], 111 340, [10, 10], 33 345, [15, 15], 22 356, [4, 4], 88 360, [8, 8], 44 368, [16, 16], 22 374, [11, 11], 33 |
390, [5, 5], 77 391, [17, 17], 22 392, [7, 7], 55 399, [3, 3, 3], 11 400, [4, 4], 99 405, [9, 9], 44 408, [12, 12], 33 414, [18, 18], 22 437, [19, 19], 22 442, [13, 13], 33 445, [5, 5], 88 445, [1, 1], 444 446, [2, 2], 222 448, [8, 8], 55 448, [4, 4], 111 450, [10, 10], 44 460, [20, 20], 22 468, [6, 6], 77 469, [7, 7], 66 476, [14, 14], 33 483, [21, 21], 22 495, [11, 11], 44 500, [5, 5], 99 504, [9, 9], 55 |
507, [1, 1, 1], 22 510, [15, 15], 33 532, [4, 4, 4], 11 534, [6, 6], 88 536, [8, 8], 66 540, [12, 12], 44 544, [16, 16], 33 556, [1, 1], 555 560, [10, 10], 55 560, [5, 5], 111 578, [17, 17], 33 585, [13, 13], 44 600, [6, 6], 99 603, [9, 9], 66 612, [18, 18], 33 616, [11, 11], 55 623, [7, 7], 88 624, [8, 8], 77 630, [14, 14], 44 646, [19, 19], 33 665, [5, 5, 5], 11 667, [1, 1], 666 668, [2, 2], 333 669, [3, 3], 222 |
670, [10, 10], 66 672, [12, 12], 55 672, [6, 6], 111 675, [15, 15], 44 680, [20, 20], 33 700, [7, 7], 99 702, [9, 9], 77 714, [21, 21], 33 720, [16, 16], 44 728, [13, 13], 55 737, [11, 11], 66 748, [22, 22], 33 765, [17, 17], 44 778, [1, 1], 777 780, [10, 10], 77 782, [23, 23], 33 784, [14, 14], 55 784, [7, 7], 111 798, [6, 6, 6], 11 800, [8, 8], 99 801, [9, 9], 88 804, [12, 12], 66 810, [18, 18], 44 816, [24, 24], 33 |
840, [15, 15], 55 850, [25, 25], 33 855, [19, 19], 44 858, [11, 11], 77 871, [13, 13], 66 884, [26, 26], 33 889, [1, 1], 888 890, [10, 10], 88 890, [2, 2], 444 892, [4, 4], 222 896, [16, 16], 55 896, [8, 8], 111 900, [20, 20], 44 918, [27, 27], 33 931, [7, 7, 7], 11 936, [12, 12], 77 938, [14, 14], 66 945, [21, 21], 44 952, [28, 28], 33 952, [17, 17], 55 979, [11, 11], 88 986, [29, 29], 33 990, [22, 22], 44 |
|||||
|
|
||
|
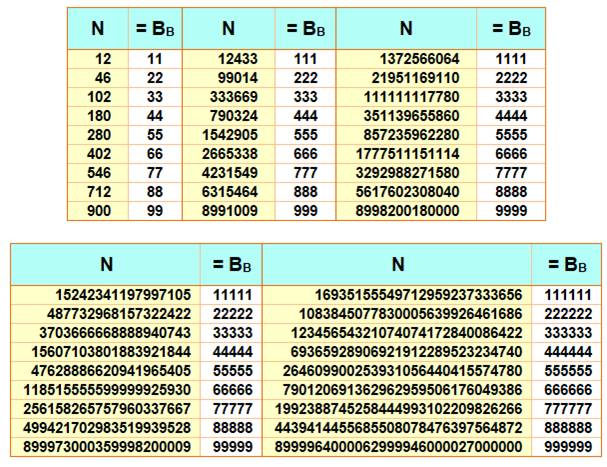
Nombres super-repdigits: (nombre brésiliens dont les
repdigits sont les mêmes que ceux de la base) Ce sont les repdigits-double pour lesquels la base est
elle-même repdigit. On y trouve par exemple: 18010 = 4444 Pour établir la liste, il suffit de calculer la valeur
décimale de a...aa…a
pour les valeurs de a successives. Ces nombres sont vite très grands! Le
premier listé 12 = 1111 est trivial, car tous les nombres n sont égaux à 11 en base (n – 1).
|
||
|
|
Ce
programme produit la
table indiquée ci-dessus. Boucle
d'exploration des nombres n puis boucle de balayage des bases de 2 à n – 2. Conversion
de n en base b sous forme d'une liste de chiffres en N. Si
la quantité de chiffres identiques
est 1, c'est que N est un repdigit;
alors on reconstitue le nombre N en base b et on le mémorise en nb. Si
ce nombre nb est égal à la base, le nombre n est converti en un repdigit dans
la base égale à ce repdigit. Le
résultat du traitement est affiché en bleu: 46 en base 10 = 22 en
base 22. |
|
Merci à Bernard Schott pour sa
définition précise des super-repdigits
Les super-repdigits sont répertoriés
en OEIS A287767
![]()
|
Retour |
||
|
Suite |
|
|
|
Voir |
|
|
|
DicoNombre |
|
|
|
Sites |
|
|
|
Cette page |
||
![]()