|
|||||||||||||||||||||||||||||
![]()
|
Inégalité de corrélation gaussienne Conjecture résolue en 2014
et officialisée en 2017. Les mesures gaussiennes jouent un rôle central en théorie des
probabilités. Leurs propriétés géométriques et analytiques ont été largement
étudiées, et mises en application dans des domaines variés (théorie des
processus, statistiques, géométrie des espaces de Banach, théorie des
algorithmes,...). Franck Barthes |
Anglais: Gaussian correlation inequality (GCI),
formerly known as the Gaussian correlation conjecture
(GCC),
|
|
||
|
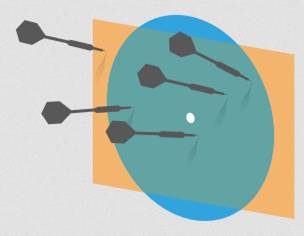
Soit deux
formes différentes centrées à l’origine et qui se chevauchent (comme le cercle et le rectangle de
l'illustration). Alors, la
proportion de fléchettes arrivant dans l’intersection des deux formes n’est jamais
inférieure au produit de la proportion des fléchettes qui arrivent dans
chacune des formes. Exemple: 65% dans le jaune et 35% dans le bleu; alors 22,75%
au moins seront dans la partie commune (0,65 x 0,35 = 0,2275). |
Source image: Wikipedia |
|
|
|
||
|
Théorème Soit Pour tous
les ensembles convexes
|
Lecture de la formule: Les mesures sur
l'intersection sont plus grandes ou égales au produit des mesures sur chacune
des parties. Note: La démonstration de Royen fait appel aux lois
gamma multivariées au sens de Krishnamoorthy et Parthasarathy et elle n'est accessible
qu'à ceux qui connaissent ce domaine. |
|
|
|
||
|
La
conjoncture de corrélation gaussienne est un théorème qui mobilise la
communauté des mathématiciens depuis les années 1950. Émise
dans un papier en 1955, puis développée par Olive Jean Dunn en 1958. Le cas
général est énoncé en 1972. Elle
n’avait jusqu’alors jamais été prouvée, malgré l’acharnement de nombreux
mathématiciens à travers le monde. |
Thomas Royen dont la carrière est consacrée aux
statistiques dans l’industrie pharmaceutique, trouve la solution en 2014. Il réécrit le problème en termes statistiques et
travaille dans le domaine qu'il maitrise. Son papier – a simple proof of the Gaussian
inequality conjecture (une simple preuve de la conjecture de corrélation gaussienne)
– est envoyée à divers mathématiciens. Donald Richard, un mathématicien de l‘Université
de Pennsylvanie, spécialiste de cette conjecture, comprend rapidement que T.
Royen vient de la résoudre. |
|
![]()
|
Suite |
|
|
Retour |
|
|
Voir |
|
|
|
|
|
Cette
page |
![]()