Nombres premiers - curiosités

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 20/12/2023 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Nombres PREMIERS
Débutants Nombres Premiers	Généralités				Glossaire Nombres Premiers
INDEX Nombres premiers	Introduction	Barre magique	Propriétés	Infinité
	Théorème des nombres premiers		Curiosités	Un
	Somme de nombres premiers		Progression arithmétique
		Sommaire de cette page >>> Somme des chiffres >>> Chiffres croissants >>> Somme paire ou impaire >>> Chaine de Cunningham >>> Différence entre premiers >>> Produits de premiers >>> Nombres premiers et leurs puissances >>> Nombres semi premiers >>> Premiers en base >>> Premiers en progression arithmétique >>> Motifs en puissance de 2 >>> Premiers, concaténation de deux nombres premiers

Nombres premiers dont les chiffres sont consécutifs

Ascendants: 23, 67, 89, 4567, 78901, 678901, 23456789, 45678901, 9012345678901, 789012345678901, 56789012345678901234567890123, 90123456789012345678901234567, 678901234567890123456789012345678901

Descendants: 43, 76543

Voir Premiers horloge

Somme des chiffres

Somme des chiffres des premiers = tout nombre hors multiples de 3

La somme des chiffres d'un nombre premier n'est jamais un multiple de 3, sinon il serait divisible par 3.

Une conjecture affirme que, hors les multiples de 3, il est toujours possible de trouver un nombre premier dont la somme des chiffres est un nombre k donné (k > 1).

Exemple avec tous les premiers < 75 (k en bleu et premiers en-dessous)

Liste des valeurs de k jusqu'au 1 000 000^e premier

2, 3, 4, 5, 7, 8, 10, 11, 13, 14, 16, 17, 19, 20, 22, 23, 25, 26, 28, 29, 31, 32, 34, 35, 37, 38, 40, 41, 43, 44, 46, 47, 49, 50, 52, 53, 55, 56, 58, 59, 61, 62

Même liste avec le nombre premier concerné
[2, 2], [3, 3], [5, 5], [7, 7], [17, 8], [19, 10], [29, 11], [59, 14], [79, 16], [89, 17], [199, 19], [389, 20], [499, 22], [599, 23], [997, 25], [1889, 26], [1999, 28], [2999, 29], [4999, 31], [6899, 32], [8999, 35], [29989, 37], [39989, 38], [49999, 40], [59999, 41], [79999, 43], [98999, 44], [199999, 46], [389999, 47], [598999, 49], [599999, 50], [799999, 52], [989999, 53], [2998999, 55], [2999999, 56], [4999999, 58], [6999899, 59], [8989999, 61], [9899999, 62], [19999999, 64], [29999999, 65], [59899999, 67], [59999999, 68], [189997999, 70], …

Liste des plus petits nombres premiers donnant les sommes successives

2, 3, 13, 5, 7, 17, 19, 29, 67, 59, 79, 89, 199, 389, 499, 599, 997, 1889, 1999, 2999, 4999, 6899, 17989, 8999, 29989, 39989, 49999, 59999, 79999, 98999, 199999, 389999, 598999, 599999, 799999, 989999, 2998999, 2999999, 4999999, 6999899, 8989999, 9899999 …

Voir Table des nombres premiers

Chiffres croissants

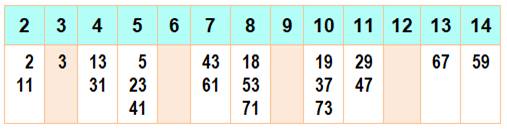
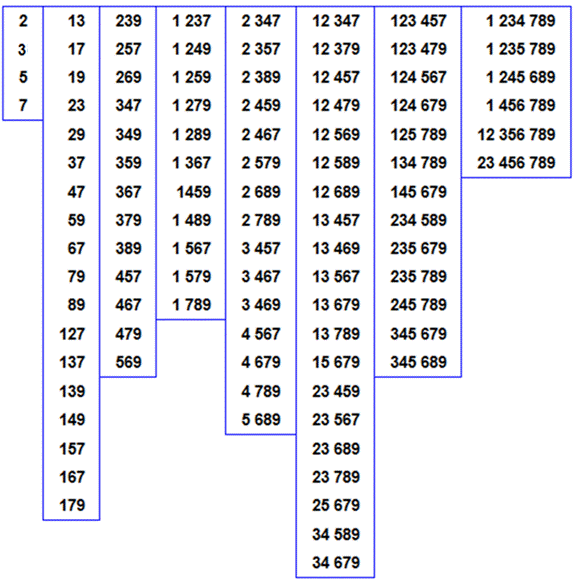
Il y a exactement cent nombres premiers dont tous les chiffres sont croissants.

On ne peut pas dépasser 123456789 et, dans cette veine, le plus grand est 23456789.

Liste des 100 nombres premiers croissants

Voir Nombre 100 / Nombres premiers horloge (chiffres qui se suivent strictement)

Somme paire ou impaire

1968: une hypothèse d'Alexandre Gelfond (russe) affirme que la somme des chiffres d'un nombre premier a autant de chance d'être paire qu'impaire.

L'exemple ci-contre liste tous les nombres premiers de 10 000 à 10 200. Il y en a exactement 23 dont la somme des chiffres est paire et 23 impaire.

2010: cette hypothèse est démontrée par Christian Mauduit et Joël Rivat.

Les outils utilisés mêlent combinatoire et analyse de Fourier discrète.

Les deux Français ont aussi trouvé la formule qui donnent des nombres premiers en binaires avec autant de 0 que de 1.

P S_PS_I

10 007 8

10 009 10

10 037 11

10 039 13

10 061 8

10 067 14

10 069 16

10 079 17

10 091 11

10 093 13

10 099 19

10 103 5

10 111 4

10 133 8

10 139 14

10 141 7

10 151 8

10 159 16

10 163 11

10 169 17

10 177 16

10 181 11

10 193 14

Total 23 23

Science et Vie – Juillet 2010

Chaine de Cunningham

1 3203 00071 95970 29781

2 6406 00143 91940 59561

3 12812 00287 83881 19121

4 25624 00575 67762 38241

5 51248 01151 35524 76481

6 1 02496 02302 71049 52961

7 2 04992 04605 42099 05921

8 4 09984 09210 84198 11841

9 8 19968 18421 68396 23681

10 16 39936 36843 36792 47361

11 32 79872 73686 73584 94721

12 65 59745 47373 47169 89441

13 131 19490 94746 94339 78881

14 262 38981 89493 88679 57761

15 524 77963 78987 77359 15521

16 1049 55927 57975 54718 31041

Chaîne de Cunningham

Séquence de k nombres premiers dont le suivant vaut le double plus un;

ou, variante : moins un.

En 1997, Tony Forbes a trouvé une chaîne du second type avec k = 16

Voir OEIS – Chaines de Cunningham / OEIS A005602

DIFFÉRENCE ENTRE PREMIERS

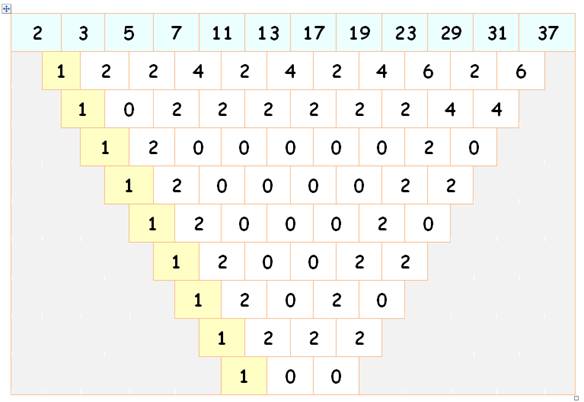
Pyramide des différences entre les nombres premiers

On conjecture que le premier 1 se poursuit indéfiniment.

Pas de démonstration.

Vérifié jusqu'à : 3 x 10¹¹.

Andrew M. Odlyzko

Suite en Conjecture de Gilbreath

PRODUITS de PREMIERS

Quels sont les nombres premiers successifs qui multipliés entre eux produisent un nombre juste avant un nombre premier ?

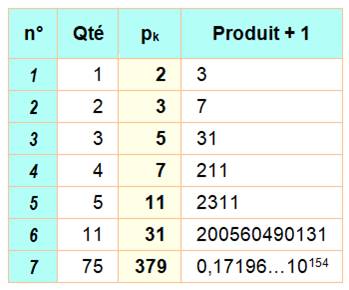
2 x 3 x 5 x …p_k +1 = P_Premier

Voir Primorielle

Nombres premiers et leurs puissances

Pour N < 100

En noir les nombres premiers.

En bleu les nombres premiers élevés au carré.

En rouge, élevé à une puissance.

Total

35 nombres premiers et leurs puissances inférieurs à 100

2	3	4	5	7	8	9	11	13	16
17	19	23	25	27	29	31	32	37	41
43	47	49	53	59	61	64	67	71	73
79	81	83	89	97

Voir Plus petits nombres possédant 2ⁿ diviseurs / Type de nombres selon facteurs

Nombres semi-premiers

Semi-premier: nombre qui n'a que deux diviseurs, pas nécessairement distincts.

Cas ou les deux diviseurs sont distincts

6	10	14	15	21	22	26	33	34	35	…
2x3	2x5	2x7	3x5	3x7	2x11	2x13	3x11	2x17	5x7

Voir Nombres semi-premiers

PREMIERS EN BASE

Certains cherchent une représentation des nombres premiers, comme la transformation en base 3, pour tenter d'en tirer une musique.

10 nombres premiers en base 3

102

111

122

201

212

1002

PREMIERS en progression arithmétique

Infinité de nombres premiers en progression arithmétique

Adrien-Marie Legendre (1752-1833) conjecture une infinité de nombres premiers pour les progressions arithmétiques dont la raison et le premier terme sont premiers entre eux.

Johann Dirichlet (1805-1859) démontre ce théorème en 1837.

Ben Green et Terence Tao démontrent en 2004 qu'il existe des chaines en progression arithmétiques aussi longue que l'on veut.

Théorème de Green-Tao (2004)

Il existe des progressions arithmétiques de nombres premiers arbitrairement longues.

Voir Terence Tao

Suite avec exemples: Nombres premiers en progression arithmétique

MOTIFS en puissances de 2

Tous les motifs pour n 100

Motif

Valeur = nombre premier

2¹ + 1

2³ + 3

2⁵ + 5

2⁹ + 9

2¹⁵ + 15

2³⁹ + 39

2⁷⁵ + 75

2⁸¹ + 81

2⁸⁹ + 89

= 3

= 11

= 37

= 521

= 32 783

= 549 755 813 927

= 37 778 931 862 957 161 709 643

= 2 417 851 639 229 258 349 412 433

= 618 970 019 642 690 137 449 562 201

Tous les nombres jusqu'à 1000 dont le carré est la concaténation de deux nombres premiers

n n²

17 , 289 , 2, 89

19 , 361 , 3, 61

23 , 529 , 5, 29

27 , 729 , 7, 29

69 , 4761 , 47, 61

73 5329 , 53, 29

77 , 5929 , 59, 29

123 , 15129 , 151, 29

177 , 31329 , 313, 29

219 47961 , 479, 61

327, 106929, 1069, 29

369, 136161, 1361, 61

381, 145161, 1451, 61

423, 178929, 1789, 29

427, 182329, 1823, 29

473, 223729, 2237, 29

519, 269361, 2693, 61

527, 277729, 2777, 29

531, 281961, 2819, 61

577, 332929, 3329, 29

623, 388129, 3881, 29

627, 393129, 3931, 29

677, 458329, 4583, 29

681, 463761, 4637, 61

723, 522729, 5227, 29

777, 603729, 6037, 29

873, 762129, 7621, 29

877, 769129, 7691, 29

973, 946729, 9467, 29

981, 962361, 9623, 61

Autres curiosités

NOMBRES PREMIERS CIRCULAIRES ou permutables

NOMBRES PSEUDO -PREMIERS ou de POULET ou NOMBRES CHINOIS

NOMBRES PREMIERS RÉSISTANTS

SÉQUENCE de NOMBRES NON PREMIERS

PREMIERS et 2ⁿ diviseurs => Plus petits nombres possédant 2ⁿ diviseurs

Produit avec des nombres premiers >>>

*Voir*	Nombres premiers en progression arithmétique Nombres premiers – Index Conjecture de Gilbreath FAQ sur les nombres premiers
*Aussi*	Liste de nombres premiers Calcul mental Curiosités de motifs et formes Divisibilité Géométrie Magie avec les nombres Nombres composés Petit théorème de Fermat Premiers en tableaux, en spirales … Représentation des nombres Théorie des nombres
*DicoNombre*	Nombre 4 Nombre 4 999
*Sites*	Pour plus de curiosités voir Pattern in prime The sum of digits of prime numbers is evenly distributed – CNRS média – 2010 OEIS A006055 - Primes with consecutive (ascending) digits OEIS A052016 - Primes with digits in descending order that differ exactly by 1
*Cette page*	http://villemin.gerard.free.fr/Wwwgvmm/Premier/curiosit.htm