|
||||||||||||||||||||||||||||||||||||||||
![]()
|
NOMBRES PREMIERS JUMEAUX Vers la démonstration de la conjecture Conjecture de
Polignac: il existe une infinité de nombres premiers jumeaux. Depuis 2013, d'énormes
progrès ont été réalisés. |
Anglais: Bounded gaps between primes / Primes in tuples /
The twin prime conjecture / Polygnac's Conjecture
|
|
||
|
Ce que nous savons de manière certaine
|
Conjectures: il existe une infinité de:
La conjecture de Polignac: il existe une infinité
de premiers avec un écart égal à h, h étant un nombre pair. La conjecture de Dickson généralise celle-ci avec
une forme en a + b.n.
Question générale
Autrement dit: quel est
l'écart m le plus petit entre deux nombres premiers consécutifs qui se répète
une infinité de fois? |
|
|
|
|||
|
CQFD |
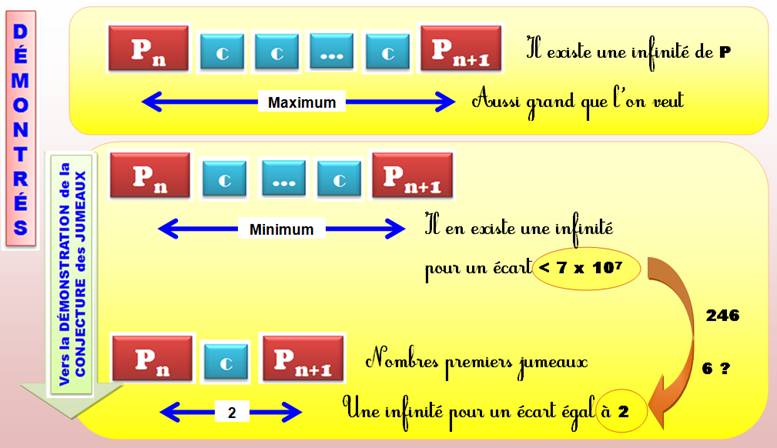
Pour démontrer la conjecture
des nombres premiers jumeaux, il faut prouver qu'il existe une infinité
de premiers avec un écart de 2. La conjecture généralisée indique
qu'il y a une infinité de premiers jumeaux avec un écart ou 2 ou toute autre
valeur possible. La conjecture date de 1849, énoncée
par Alphonse de Polignac (1826-1863). |
||
|
Les progrès après 2000 |
|||
|
D.
A. Goldston, J. Pintz and C. Y. Yildirim 2009 |
|
||
|
Yitang Zhang (né en 1955) 2013 Mathématicien de l'Université du New
Hampshire |
Il existe une infinité de
premiers tels que l'écart entre eux est inférieur à 7
x 107.
|
||
|
James Maynard 2013
Né en 1987 |
|
||
|
Polymath8 en avril 2014 Équipe collaborative sur Internet |
|
||
|
Idem avec James
Maynard and Terence
Tao |
|
||
|
|
|
||
|
|
||
|
Will
Sawin de Columbia University et Mark Shusterman del'University de Wisconsin,
Madison démontre la conjecture limitée aux corps finis. Si la
démonstration est limité aux corps finis, elle est étendue à tous les écarts
possibles entres nombres premiers. En
supplément, elle donne la quantité de premiers jumeaux dans un intervalle. |
La démonstration s'applique aux corps
finis. Mais même dans ce monde limité (non-infini), elle représente une
avancée majeure. Les mathématiciens espèrent que la compréhension
dans le monde fini aidera à la transposition dans le monde infini. |
|
|
Une idée des corps fini (finite field) et de leur exploitation pour cette
démonstration. On
connait le monde des congruences
qui limite la quantité de nombres à une certaines valeur (comme l'horloge est
limitée à 12). Oups ! Ici,
tous les nombres sont divisibles. Donc pas
de nombres premiers ! |
Dans un corps
fini de 5, la somme 4 + 3 vaut 2. Divisibilité – Exemple 2, 7, 12 sont équivalent et 12 / 3 = 4 donc 7 / 3 = 4 dans le monde mod 5. |
|
|
Passage aux polynômes Chaque
coefficient du polynôme représente un nombre du corps |
2x + 1 => {2, 1} x2 + x +
2 => {1, 1, 2} |
|
|
Un polynôme premier est un
polynôme qui n'est pas factorisable. La conjecture
devient: il existe une infinité de pairs de polynômes premiers qui différent
de x ou de toute autre valeur. |
x² – 1 = (x –
1)(x+1) non premier x² + x + 2 est
premier x² + 2x + 2 est
premier jumeau du précédent (addition de x) |
|
Passage aux polynômes et à la géométrie
|
La
démarche entreprise ici n'est pas nouvelle. Dans les années 1940, André Weil
inventa un moyen de traduire de passer à une arithmétique des nombres finis
pour étudier les nombres entiers. Il en a tiré une démonstration dans le
domaine de l'hypothèse
géométrique de Riemann Cette
preuve, ainsi que toute une série de conjectures supplémentaires établies par
Weil - les conjectures de Weil - établissent des champs finis comme un
paysage riche pour la découverte mathématique. |
|
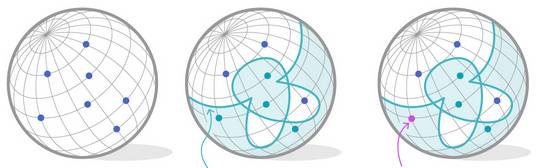
Passage à la géométrie Les
coefficients du polynôme servent de coordonnées de points dans un espace de
dimension égale au degré n du polynôme. |
Une frontière est dessinée séparant les polynômes ayant une
quantité impaire de facteurs de ceux qui ont une quantité paire. La frontière est de dimension n – 1 . |
||
|
Illustration avec le degré 1
Source dessin Quantamagazine |
|||
|
Le polynôme 2x + 3 est représenté par un point sur la sphère en 2D. |
La ligne sépare les polynômes factorisables en quantité impaire ou
paire. |
Recherche des polynômes
premier (dans la zone impaire). |
|
|
Fonction de Moebius |
La fonction
de Moebius indique si le polynôme possède un nombre pair de facteurs
(elle vaut alors 1), ou un nombre impair (-1) ou encore si elle possède des facteurs
multiples (0). La courbe qui se dessine est tortueuse. Les endroits où elle se recoupe
correspond aux facteusr répétés (singularités). Idem pour dimesnsions
supérieures. |
||
|
Sawin et Shusterman |
Ces deux mathématiciens ont trouvé un moyen pour découper la courbe
frontière (ou dimension supérieure) en plusieurs segmenst plus faciles à
étudier. |
||
Ce paragraphe est largement inspiré de l'article de
Quantmagazine référencé en lien
![]()
|
Voir |
|
|
Livre |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/aNombre/TYPMULTI/Premjuco.htm |
![]()