![]()
|
![]()
|
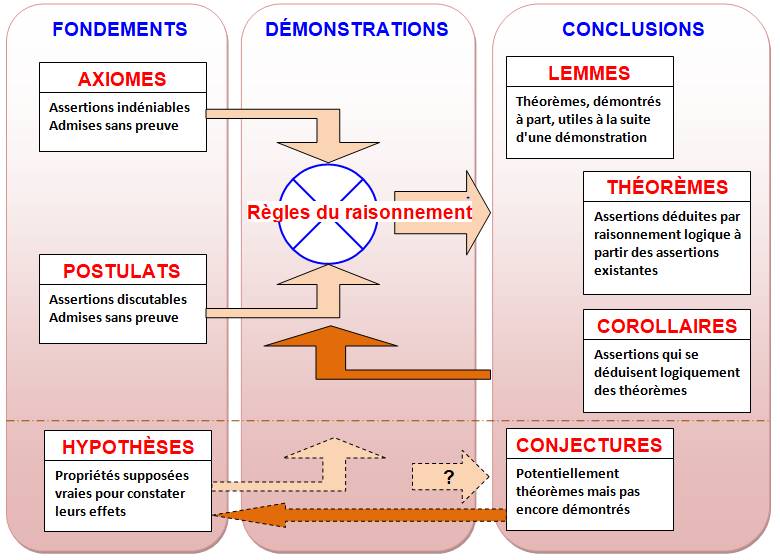
Termes
utilisés en mathématique (sauf indications particulières) |
|
|
|
Les
briques |
||
|
Définition (definition) Énoncé (statement) |
Énoncé
qui précise la nature d'une entité mathématique.
Un nombre premier
est un entier naturel ayant exactement deux diviseurs lui-même et 1. On définit le triangle
isocèle comme triangle qui a deux côtés égaux (on dit: de mêmes mesures ou
isométriques). Cependant,
il existe des termes primitifs que l'on ne peut pas définir comme: point,
droite, égal … disait Pascal. |
|
|
Proposition (proposition) |
Énoncé
d'un fait, sans que l'on sache son degré de véracité Une proposition indécidable. Calcul propositionnel. |
|
|
Assertion (assertion) |
Proposition
avancée comme vraie dans le cadre d'une théorie. 2 + 2 = 4 est une assertion vraie dans la théorie des nombres. Proposition
énoncée sous forme affirmative ou négative que l'on cherchera certainement à
démontrer. En
logique, il s'agit d'une expression vraie. Les assertions sont les entrées
d'un processus logique de déduction. |
|
|
Hypothèse (hypothesis) |
Assertion
posée comme vraie pour conduire un raisonnement, un calcul. |
|
|
Axiome (axiom) |
Une
assertion évidente, universelle et non démontrable, posée comme point de
départ à une théorie mathématique, à une axiomatique. Vérité
première indémontrable. Les axiomes
doivent s'accorder aux définitions données et permettre de donner un point de
départ cohérent à la théorie proposée. Les axiomes
doivent être vérifiés, les théorèmes démontrés. La pertinence
d'une théorie dépend de la pertinence de ses axiomes. Axiomes
de Peano en arithmétique. Axiome
du choix en théorie des ensembles. Les
axiomes de Zermelo-Fraenkel |
|
|
Postulat (postulate) |
Un
postulat est un axiome historique. Aucune
différence sémantique avec l'axiome, sinon que l'assertion est peut-être
moins évidente à admettre comme vraie. Parfois
utilisé comme un axiome temporaire, une assertion à admettre tant qu'elle
n'est pas démontrée, mais nécessaire à la conduite d'un raisonnement.. Ce mot
n'est plus utilisé en mathématique; il est plutôt remplacé par hypothèse ou
conjecture. Il est toujours utilisé en physique théorique ou en philosophie. Un postulat fondamental de la philosophie de Jules Vuillemin consiste à
poser une relation intime entre mathématiques et philosophie. Le cinquième postulat
d'Euclide relatif aux droites parallèles est rebaptisé aujourd'hui:
axiome d'Euclide ou axiome des parallèles. |
|
|
Principe (principle) |
Utilisé
en math, mais non recommandé, pour exprimer une idée simple, sinon elle devient théorème. En
physique, un principe est souvent d'abord énoncé comme un postulat et il peut
devenir un théorème, mais il garde le nom de principe. Principe
d'Archimède devenu le théorème d'Archimède Principe de causalité: tout phénomène a une cause. Principe
d'exclusion de Pauli (Pauli
exclusion principle). |
|
|
Conjecture (conjecture) |
Assertion
vérifiée comme vraie dans tous les cas connus, mais non encore démontrée. |
|
|
Les
conclusions |
|
|
Lemme (lemma = helping theorem) |
Un mini-théorème
préalable à une démonstration. Un résultat intermédiaire nécessaire pour
conduire une démonstration complète. On prend
la peine d'en faire sa démonstration séparément pour ne pas alourdir la
démonstration complète. Le
résultat ne présente pas un intérêt digne de passer à la postérité sous la
forme d'un théorème; toutefois, certains sont devenir célèbres. Lemme
d'Euclide (qui mériterait le nom de théorème d'Euclide). |
|
Théorème (theorem) |
Une
assertion démontrée Sa
validité est acquise une fois pour toute, dans le cadre de la théorie
mathématique dont il fait partie. Il existe une infinité de
nombres premiers. Théorème
fondamental de l'arithmétique. Théorème fondamental de
l'algèbre. Théorème
d'incomplétude de Gödel. |
|
Corollaire (corollary) Réciproque (converse) |
Un théorème
qui se déduit immédiatement d'un autre théorème. Une conséquence pratiquement
directe de ce théorème. Souvent
un cas particulier du théorème ou alors la réciproque d'un théorème
(implication réciproque). Théorème: dans un
cercle, l'angle
inscrit est égal à la moitié de l'angle au centre. Corollaire: tout angle qui
intercepte un diamètre est droit. Théorème: un triangle qui
a deux côtés égaux (isométriques), possède aussi deux angles égaux. Réciproque: un triangle
qui a deux angles égaux, présente aussi deux côtés égaux. |
|
Règle (rule) |
Un
théorème érigé en formule pratique La règle de Cramer
est utile à la résolution d'un système d'équations. |
|
Loi (law) |
Un
théorème applicable dans de nombreux cas. L’addition
dans l’ensemble des nombres
naturels est une loi
de composition interne dans N. Note: une loi
peut également désigner une définition La
loi normale en probabilité. |
|
Identité (identity) |
Un
théorème mis sous la forme d'une égalité valable quelles que soient les valeurs
des variables. Identités
remarquables: identités algébriques Note: une
identité est aussi une relation entre constantes. Ce peut être également une
relation introduisant une définition. |
|
Le
tout |
|
|
Axiomatique |
Elle
rassemble et structure les axiomes et les principes de base d'une science. Système
d'axiomes de la géométrie d'Euclide La théorie axiomatique des groupes
abstraits |
|
Théorie |
Ensemble
d’affirmations dont certaines sont des axiomes et les autres des théorèmes
démontrables à partir de ces axiomes et au moyen de règles de la logique. La
théorie des cordes (en physique quantique) . |
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Referenc/Vocabula/GlosT/Theoreme.htm |
![]()