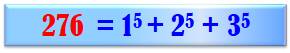|
Édition du: 27/03/2025 |
|
INDEX |
n = somme de puissances |
||
|
Somme de 4 carrés |
Somme de n puissances |
||
Faites un double-clic pour un retour en haut de page
![]()
|
Nombres P5 Plusieurs points
d'intérêts avec les puissances des nombres entiers:
On s'intéresse
aux sommes de puissances cinquièmes des entiers positifs, de même que les
entiers relatifs. Alors les puissances cinquièmes sont positives ou négatives.
Pour une
introduction et certaines curiosités avec les puissances cinquièmes, voir la page générale: Exemples
|
||
|
|
Sommaire de cette page >>> Puissances cinquièmes >>> Cas des nombres 100 et 952 (exemples) >>>
Tables des kP5 avec k nombres positifs |
Débutants Glossaire |
Voir Nombre 5
|
Théorème de Waring pour la
puissance 5 Tout nombre entier est décomposable en somme d'au plus 37 puissances
cinquièmes Les nombres suffisamment grands sont décomposables
en sommes d'au plus 17 puissances
cinquièmes. |
État des connaissances g(n) = 37 G(n) ≤ 17 Au-delà de 87 918, on
conjecture que les nombres sont sommes d'au plus 17
puissances cinquièmes positives. Au-delà de 77 529 941, on
conjecture que les nombres sont sommes d'au plus 10
puissances cinquièmes positives |
|
|
Il est classique de s'intéresser aux partitions
des nombres en cinq puissances cinquièmes.
Les nombres peuvent être répétés ou distincts. Et aussi, trouver une puissance cinquième
décomposable en cinq puissances cinquièmes. |
1 934 917 632 = 725 = 195 + 435 + 465
+ 475 + 675 |
|
|
Nombre 100 La méthode pour calculer la partition du nombre 100
en puissance de 5 consiste naturellement à déduire le maximum de fois les
puissances décroissantes. Aucun puissance de 3; 3 puissance de 2 convient
et il reste 4. Soit la partition: |
100 = 3 × 25 + 4 × 15 = 3 × 32 + 4 |
|
|
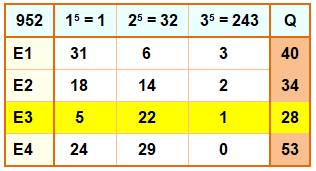
Nombre 952 Ce nombre nous réserve une surprise ! La méthode par puissances décroissantes donne
(ligne essai E1): On sait que Q ne devrait pas dépasser 37. Il
faut chercher une autre partition en
diminuant la quantité de termes en 35. L'essai E2 donne: L'essai E3 donne: |
952 = 35
+ 22 × 25 + 5 × 15 = 243 + 22 × 32 + 5 |
|
|
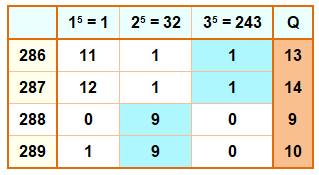
Autres exemples de minimisation Le nombre 287 est supérieur à 35 = 243
et sa partition est: La partition du suivant pourrait être: Mais, il est possible de diminuer la quantité de
termes: |
|
|
|
Autre exemple La méthode par puissances dégressives donne 42
termes pour 3000, alors qu'en retirant
une puissance de 4 et en l'exprimant en puissances de 3, la partition
passe à 10 termes seulement. |
3000 = 2×45 +
3×35 +
6×25 +
31×15 (42 termes) 3000 = 1×45 +
8×35 +
1×25
+ 0×15 (10 termes) |
|
|
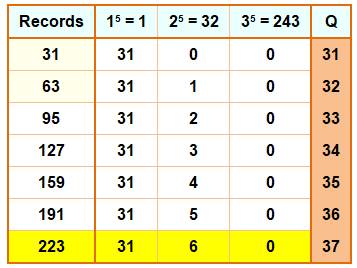
Avec 37 termes, le maximum Le tableau donne les plus petits nombres dont les
partitions nécessitent Q termes par ordre croissant. Le nombre 223 est le plus
petit entier, et le seul, qui nécessite 37 termes pour sa partition
en puissances cinquièmes positives. Le nombre suivant passe à exactement 7 fois la
puissance 5 de 2: |
223 = 6 × 25 + 31 × 15 = 6 × 32 + 31 |
|
|
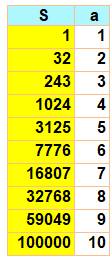
P5 |
|
0, 1, 32, 243, 1024, 3125, 7776, 16807, 32768, 59049, 100000, 161051,
248832, 371293, 537824, 759375, 1048576, 1419857, 1889568, 2476099, 3200000, 4084101,
5153632, 6436343, 7962624, 9765625, 11881376, 14348907, 17210368, 20511149,
… OEIS
A000584 |
|
|
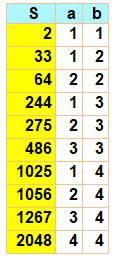
2P5 |
|
2, 33, 64, 244, 275, 486, 1025, 1056, 1267, 2048, 3126, 3157, 3368,
4149, 6250, 7777, 7808, 8019, 8800, 10901, 15552, 16808, 16839, 17050, 17831,
19932, 24583, 32769, 32800, 33011, 33614, 33792, 35893, 40544, 49575, 59050,
59081, 59292, 60073, 62174, 65536, 66825, 75856, … OEIS A003347 |
|
|
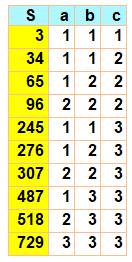
3P5 |
|
3, 34, 65, 96, 245, 276, 307, 487, 518, 729, 1026, 1057, 1088, 1268,
1299, 1510, 2049, 2080, 2291, 3072, 3127, 3158, 3189, 3369, 3400, 3611, 4150,
4181, 4392, 5173, 6251, 6282, 6493, 7274, 7778, 7809, 7840, 8020, 8051, 8262,
8801, 8832, 9043, 9375, 9824, 10902, 10933, … OEIS
A003348 |
|
|
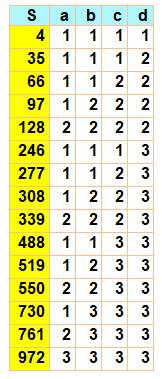
4P5 |
|
4, 35, 66, 97, 128, 246, 277, 308, 339, 488, 519, 550, 730, 761, 972,
1027, 1058, 1089, 1120, 1269, 1300, 1331, 1511, 1542, 1753, 2050, 2081, 2112,
2292, 2323, 2534, 3073, 3104, 3128, 3159, 3190, 3221, 3315, 3370, 3401, 3432,
3612, 3643, 3854, 4096, 4151, 4182, 4213, 4393,
4424, 4635, 5174, 5205, 5416, 6197, 6252, 6283, 6314, 6494, 6525, 6736, 7275,
7306, 7517, 7779, 7810, 7841, 7872, 8021, 8052, 8083, 8263, 8294, 8298, 8505,
8802, 8833, 8864, 9044, 9075, 9286, 9376, 9407, 9618, 9825, 9856, 10067,
10399, 10848, 10903, 10934, 10965 … OEIS A003349 |
|
|
5P5 |
|
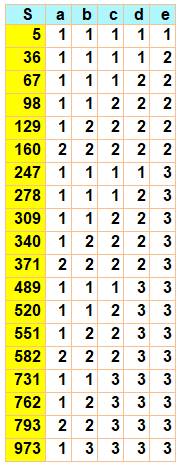
5, 36, 67, 98, 129, 160, 247, 278, 309, 340, 371, 489, 520, 551, 582,
731, 762, 793, 973, 1004, 1028, 1059, 1090, 1121, 1152, 1215, 1270, 1301,
1332, 1363, 1512, 1543, 1574, 1754, 1785, 1996, 2051, 2082, 2113, 2144, 2293,
2324, 2355, 2535, 2566, 2777, 3074, 3105, 3129, 3136, 3160, 3191, 3222, 3253,
3316, 3347, 3371, 3402, 3433, 3464, 3558, 3613, 3644, 3675, 3855, 3886, 4097,
4097, 4128, 4152, 4183, 4214, 4245, 4339, 4394, 4425, 4456, 4636, 4667, 4878,
5120, 5175, 5206, 5237, 5417, 5448, 5659, 6198, 6229, 6253, 6284, 6315, 6346,
6440, 6495, 6526, 6557, 6737, 6768, 6979, 7221, 7276, 7307, 7338, 7518, 7549,
7760, 7780, 7811, 7842, 7873, 7904, 8022, 8053, 8084, 8115, 8264, 8295, 8299,
8326, 8330, 8506, 8537, 8541, 8748, 8803, 8834, 8865, 8896, 9045, 9076, 9107,
9287, 9318, 9322, 9377, 9408, 9439, 9529, 9619, 9650, 9826, 9857, 9861, 9888,
10068, 10099, 10310, 10400, 10431, 10642, 10849, 10880, 10904, 10935, 10966,
10997…. OEIS A003350 |
|
|
5P5 2 fois et plus |
4097, 51446, 51477, 51688, 52469, 54570, 59221, 68252, 68905, 84213,
110494, 131104, 151445, 212496, 300277, 325174, 325713, 355114, 422135, 422738,
589269, 637418, 794434, 810820, 876734, 876765, 876976, 877757, 879858,
884509, 893540, 909501, 924912, 935782, 976733, 995571, 1037784, 1083457, …. OEIS A342685 |
|
5P5 3 fois et plus |
13124675, 28055699, 50043937, 52679923, 53069024, 55097976, 57936559,
60484744, 62260463, 62445305, 70211956, 73133026, 79401728, 80368962,
84766210, 88512249, 93288865, 98824300, 106993391, 113055482, 117173891,
120968132, 123383875, 126416258, 131106051, 131529588, 132022925, OEIS
A342687 |
|
Nombres
sommes de jusqu'à 15 puissances 5 |
|||
|
1 à 15 P5 49 nombres sur 100 ont des partitions
avec moins de 16 termes. Les autres nécessitent plus
de termes. Pae exemple de 15 à 32, il
faut ajouter des 1. Ainsi, 31 nécessite 31 termes. |
|
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 32, 33, 34, 35,
36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 64, 65, 66, 67, 68, 69, 70, 71,
72, 73, 74, 75, 76, 77, 96, 97, 98, 99 |
|
Haut de page (ou
double-clic)
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |